Section 4.1 The Unit Circle and Radians
A circle may be small, yet it may be as mathematically beautiful and perfect as a large one. — Isaac D'Israeli, British writer, scholar and man of letters, 1766 – 1848
Puzzle: Illustrated below is a quarter-circle, containing two semicircles of smaller circles. Prove that the red segment has the same area as the blue.
See Figure 4.1.
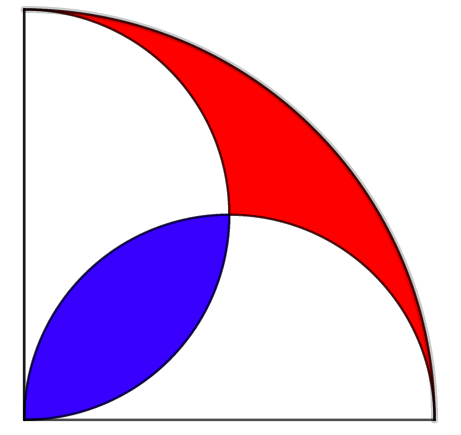
Suppose that the radius of the quarter–circle equals to \(r\text{.}\) Then the area of the quarter–circle equals to
Observe that the diameters of smaller circles are of the length equal to \(\frac{r}{2}\text{.}\) Hence the area of each of the two semicircles is given by
Let \(R\) be the area of the part of the quarter-circle that is not covered by the two semicircles and let \(B\) be the are of the part of the quarter-circle where the two semicircles overlap. Then the are of the quarter–circle is given by
Since \(\displaystyle A=\frac{1}{4}\cdot r^2\pi\) it follows that \(R-B=0\) and \(R=B\text{.}\)
Unit Circle. The unit circle is the circle of radius one centred at the origin \((0, 0)\text{.}\) See Figure 4.2.
Example 4.1.1. Points on the unit circle.
Which of the following points does not belong to the unit circle.
\(\displaystyle (1,0)\)
\(\displaystyle \displaystyle \left(\frac{1}{2},\frac{\sqrt{3}}{2}\right)\)
\(\displaystyle \displaystyle \left(-\frac{\sqrt{2}}{2},\frac{\sqrt{2}}{2}\right)\)
\(\displaystyle \displaystyle \left(-\frac{1}{2},-\frac{\sqrt{3}}{2}\right)\)
\(\displaystyle \displaystyle \left(\frac{\sqrt{2}}{2},-\frac{\sqrt{3}}{2}\right)\)
Note that for the point \(\displaystyle \left(\frac{\sqrt{2}}{2},-\frac{\sqrt{3}}{2}\right)\) we have
Hence this point does not belong to the unit circle.
Will Go Round In Circles –One:
Will Go Round In Circles– Two: See Figure 4.4 – Figure 4.7.

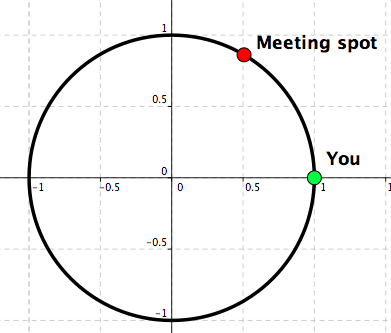

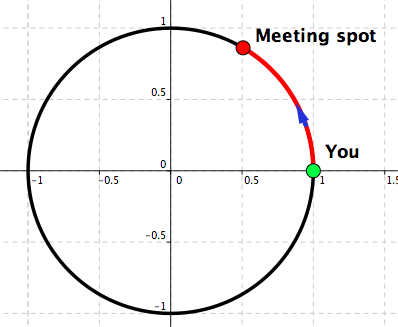

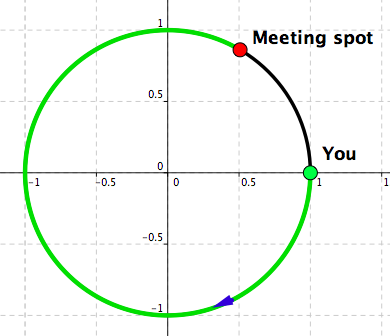

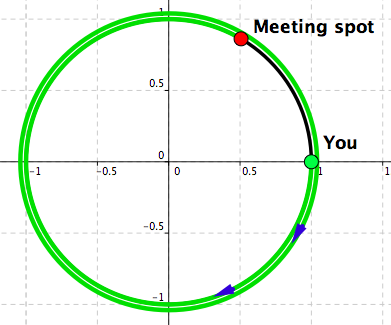
Observation: There are multiple ways of going from one point on the circle to another point on the circle, while staying on the circle all the time.
Reminder: The circumference of a circle with radius \(r\) is given by
The circumference of the unit circle is given by
See Figure 4.8.
Two directions. See Figure 4.9 and Figure 4.10.
Example 4.1.2. Sign and length = Signed length.
Example 4.1.3. Signed length.
Which number is associated with the blue arc oriented by the red arrow?
Observe that the point \(\displaystyle \left(\frac{\sqrt{2}}{2},\frac{\sqrt{2}}{2}\right)\) belongs to the line \(y=x\text{.}\)
Now, use the symmetry to conclude that \(\displaystyle \left(\frac{\sqrt{2}}{2},\frac{\sqrt{2}}{2}\right)\) is the midpoint of the arc of the unit circle that belongs to the first quadrant.
It follows that the length of the blue arc equals to
Because of the negative orientation, conclude that the number that corresponds to the blue arc is \(\displaystyle -\frac{7\pi}{4}\text{.}\)
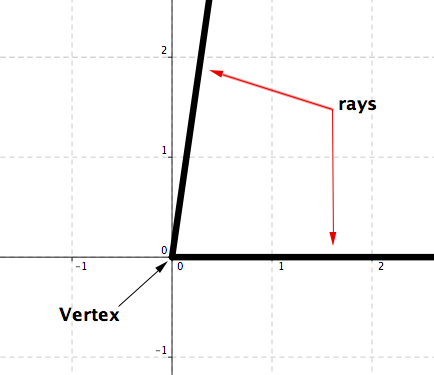
Angles: An angle is the figure formed by two rays, called the sides of the angle, sharing a common endpoint, called the vertex of the angle.
See Figure 4.14.
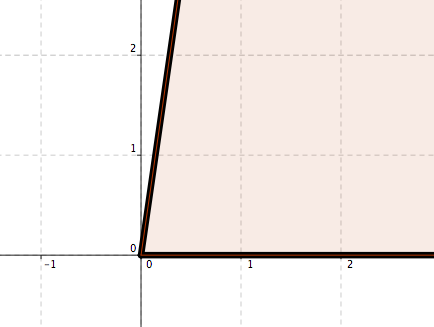
One angle – Two regions. See Figure 4.15.
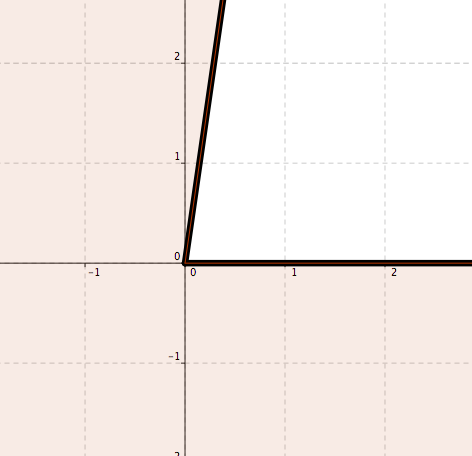
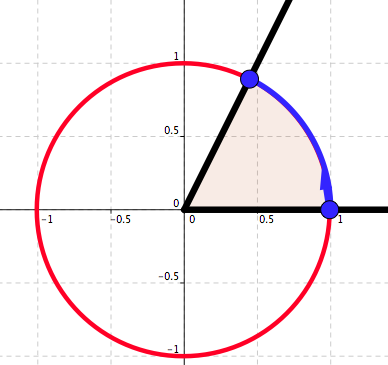
Angles and numbers - One. Consider an angle with the vertex at the origin and having the positive part of the \(x\)–axis as one ray. Angle's rays intersect the unit circle. See Figure 4.16.
Angles: An angle is the figure formed by two rays, called the sides of the angle, sharing a common endpoint, called the vertex of the angle.
See Figure 4.14.

One angle – Two regions. See Figure 4.15.


Angles and numbers - One. Consider an angle with the vertex at the origin and having the positive part of the \(x\)–axis as one ray. Angle's rays intersect the unit circle. See Figure 4.16.

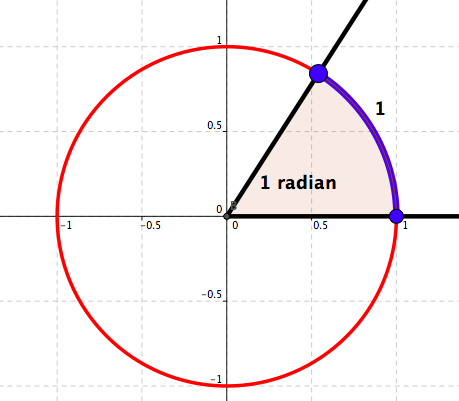
Angles and numbers - Two. We say that the angle that is associated with the arc of the length 1 measures 1 radian. See Figure 4.20.
MUST KNOW!
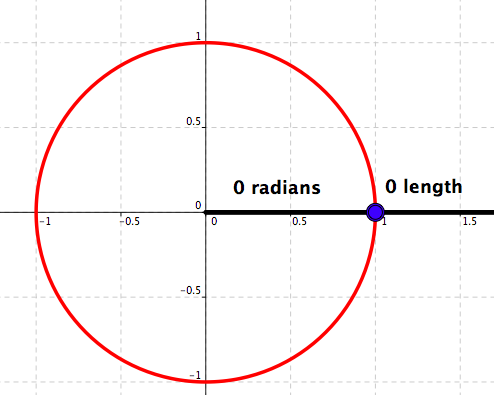
Measure in radians: \(0\)
Measure in degrees: \(0\)
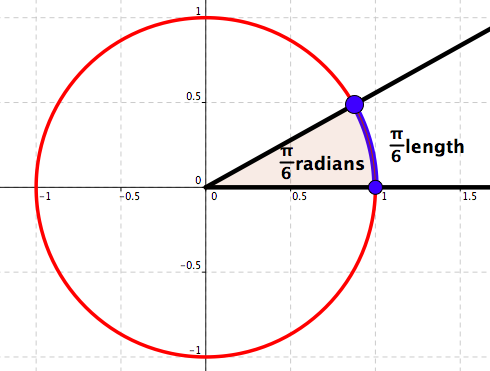
Measure in radians: \(\frac{\pi}{6}\)
Measure in degrees: \(30\)
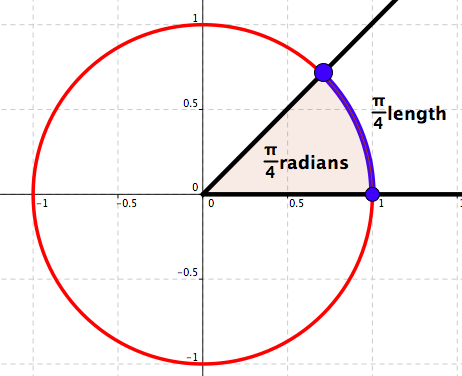
Measure in radians: \(\frac{\pi}{4}\)
Measure in degrees: \(45\)
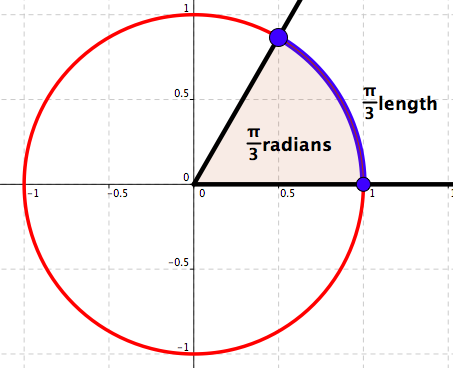
Measure in radians: \(\frac{\pi}{3}\)
Measure in degrees: \(60\)
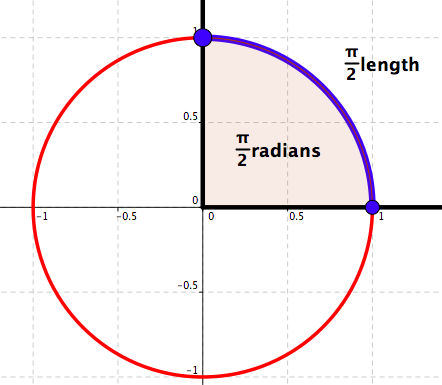
Measure in radians: \(\frac{\pi}{2}\)
Measure in degrees: \(90\)

Measure in radians: \(\frac{2\pi}{3}\)
Measure in degrees: \(120\)
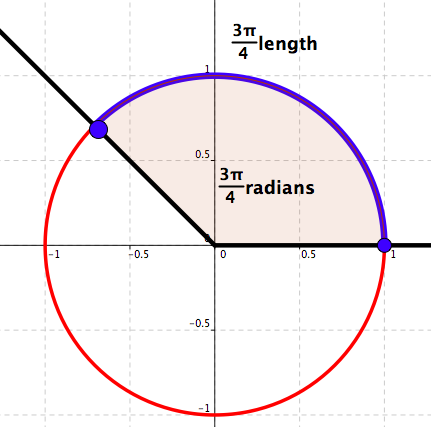
Measure in radians: \(\frac{3\pi}{4}\)
Measure in degrees: \(135\)
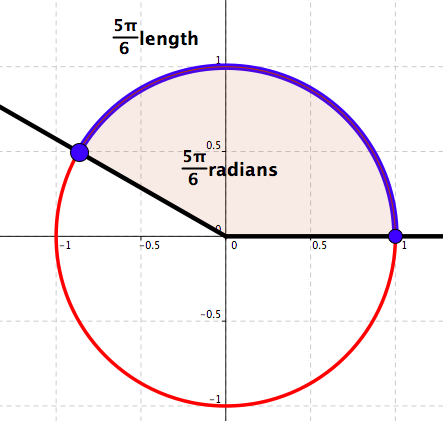
Measure in radians: \(\frac{5\pi}{6}\)
Measure in degrees: \(150\)
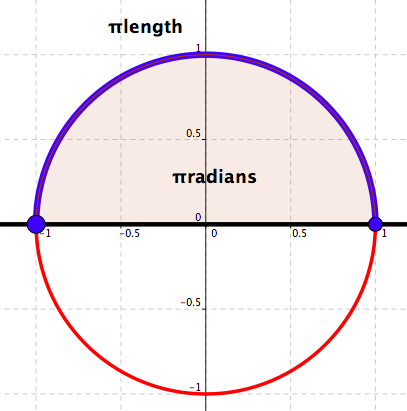
Measure in radians: \(\pi\)
Measure in degrees: \(180\)
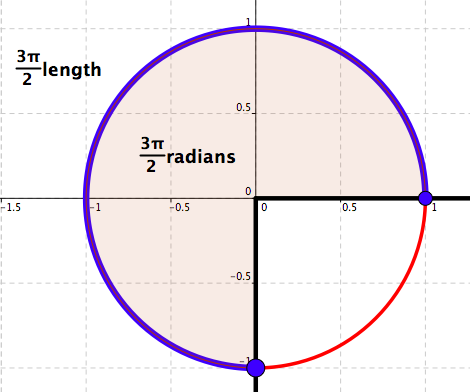
Measure in radians: \(\frac{3\pi}{2}\)
Measure in degrees: \(270\)
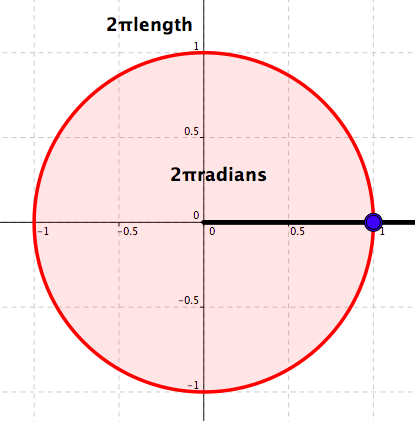
Measure in radians: \(2\pi\)
Measure in degrees: \(360\)
Angles and numbers – Three. Starting at the point \((1,0)\text{,}\) to each real number \(x\) we associate the unique point \(X\) on the unit circle so that \(X\) is the end point of the arc of the signed length \(x\text{.}\)
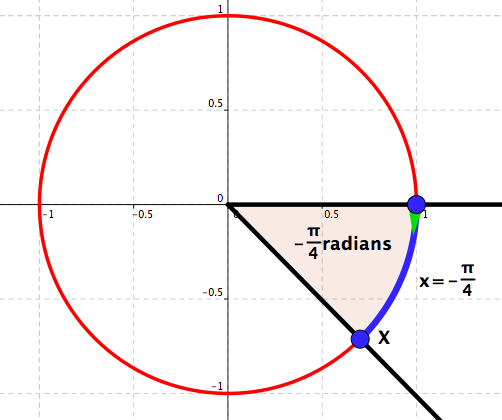
Example 4.1.4. Four angles.
Draw the angles:
\(\displaystyle \displaystyle \alpha =\frac{4\pi}{3}\)
\(\displaystyle \displaystyle \beta =-\frac{2\pi}{3}\)
\(\displaystyle \displaystyle \gamma =\frac{9\pi}{4}\)
\(\displaystyle \displaystyle \delta =-\frac{15\pi}{4}\)
-
See Figure 4.22.
Figure 4.22. \(\displaystyle \alpha =\frac{4\pi}{3}\text{.}\) -
See Figure 4.23.
Figure 4.23. \(\displaystyle \beta =-\frac{2\pi}{3}\text{.}\) -
See Figure 4.24.
Figure 4.24. \(\displaystyle \gamma =\frac{9\pi}{4}\text{.}\) -
See Figure 4.25.
Figure 4.25. \(\displaystyle \delta =-\frac{15\pi}{4}\text{.}\)
