Composition of Functions

Section 1.5 Composition of Functions

No one is an artist unless he carries his picture in his head before painting it, and is sure of his method and composition. — Oscar–Claude Monet, a founder of French Impressionist painting, 1840–1926

Problem: If $f(x)=x^2$ and $g(x)=2x$ what is $g(f(3))\text{?}$

Consider the following example: The Northwest Coast people have a long tradition of making various products for every day use from cedar roots. Generally, one can divide this procedure in two phases:

Gathering and processing cedar roots.
Weaving of an object.

Note: Different parts of the cedar are used to make different objects. For example, the inner cedar bark is commonly used for making traditional hats and skirts. The very outer bark is used to make canoe balers. Some hats are made from spruce roots.

Two illustrations and two questions:

Consider the following three functions:

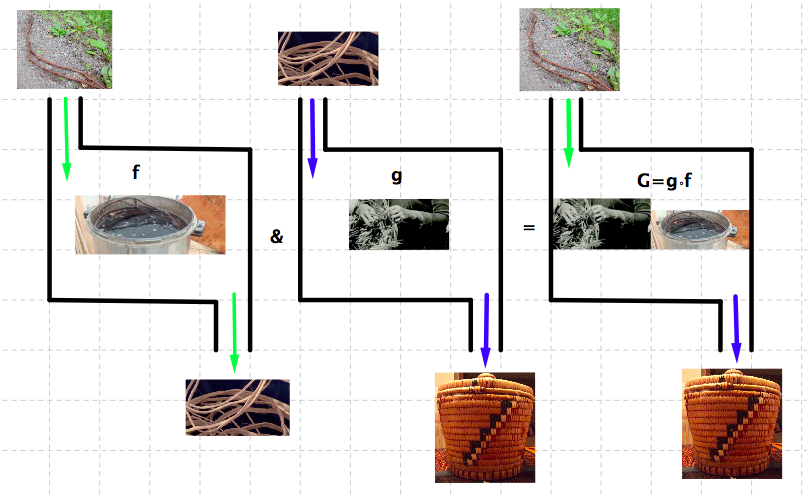
Figure 1.62. The function $f$ represents the procedure in which raw cedar roots are inputs and processed cedar roots are outcomes. The function $g$ represents the procedure of weaving a basket. The function $G=g\circ f\text{,}$ the composition of $f$ and $g\text{,}$ represents the procedure in which raw cedar roots are inputs and baskets are outcomes.
Question: Does $f\circ g$ make sense?
Consider the following three functions:

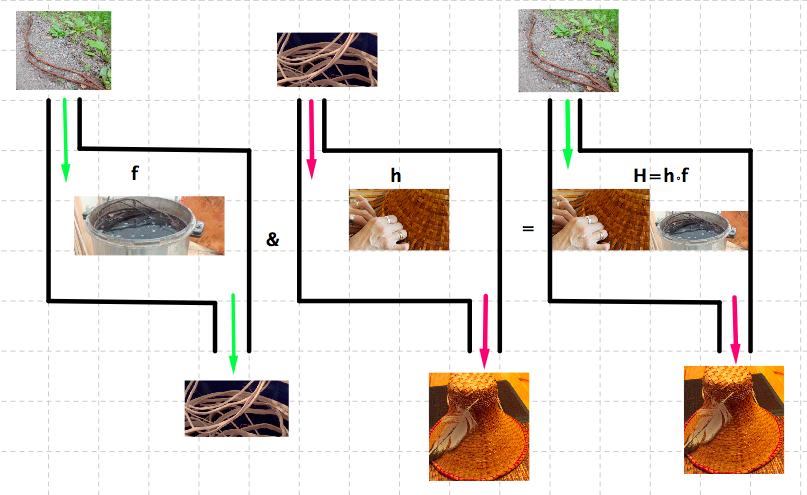
Figure 1.63. The function $f$ represents the procedure in which raw cedar roots are inputs and processed cedar roots are outcomes. The function $h$ represents the procedure of weaving a hat. The function $H=g\circ f\text{,}$ the composition of $f$ and $h\text{,}$ represents the procedure in which raw cedar roots are inputs and hats are outcomes
Question: Is it true that $g\circ f=h\circ f\text{?}$

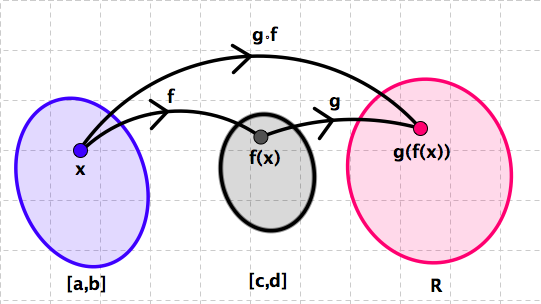
Composition of Functions: Let $f:[a,b]\to [c,d]$ and $g:[c,d]\to \mathbb{R}$ be two functions. We define a new function $F:[a,b]\to \mathbb{R}$ by

\begin{equation*} F(x)=g(f(x)), x\in [a,b]. \end{equation*}

The function $F$ is called the composition of $g$ and $f$ and it is denoted by $F=g\circ f\text{.}$

Figure 1.64. The composition of the functions $f$ and $g$ associates $x$ from the domain of $f$ with $g(f(x))$ from the range of $g\text{.}$

Example 1.5.1. Composition – One.

If $f(x)=x^2$ and $g(x)=2x\text{,}$ what is $g(f(3))\text{?}$ What is $f(g(3))\text{?}$

Solution

Since $f(3)=3^2=9\text{,}$ it follows that $g(f(3))=g(9)=18\text{.}$

Similarly, $f(g(3))=f(6)=36\text{.}$

Example 1.5.2. Composition – Two.

Find $(g\circ f)(x)$ and $(f\circ g)(x)$ and their domains if:

$f(x)=3x+2$ and $\displaystyle g(x)=-\frac{3}{4}x+\frac{1}{2}\text{.}$
$f(x)=2x+1$ and $\displaystyle g(x)=\frac{1}{x}\text{.}$

Solution

Observe that both $f$ and $g$ are defined on the set of all real numbers. This implies that the functions $(g\circ f)(x)$ and $(f\circ g)(x)$ are defined on the set of all real numbers.

By definition:

\begin{equation*} (g\circ f)(x)=g(f(x))=g(3x+2)=-\frac{3}{4}(3x+2)+\frac{1}{2}=-\frac{9x}{4}-1 \end{equation*}

and

\begin{equation*} (f\circ g)(x)=f(g(x))=f\left( \frac{3}{4}x+\frac{1}{2}\right)=3\cdot\left(-\frac{3}{4}x+\frac{1}{2}\right)+2=-\frac{9x}{4}+\frac{7}{2}. \end{equation*}
Observe that $f$ is defined on the set of all real numbers but that the domain of $g$ is the set

\begin{equation*} \mathbb{R}\backslash \{0\}=\{x\in \mathbb{R}:x\not= 0\}. \end{equation*}

This implies that the function $(g\circ f)(x)=g(f(x))$ is not defined at $x\in\mathbb{R}$ for which $f(x)=0$

From

\begin{equation*} f(x)=0\Leftrightarrow 2x+1=0 \Leftrightarrow x=-\frac{1}{2} \end{equation*}

it follows that the domain of the function $(g\circ f)(x)$ is the set $\mathbb{R}\backslash \left\{-\frac{1}{2}\right\}=\left\{x\in \mathbb{R}:x\not=-\frac{1}{2}\right\}\text{.}$

We observe that the domain of the function $(f\circ g)(x)$ is the same as the domain of the function $g\text{.}$

By definition:

\begin{equation*} (g\circ f)(x)=g(f(x))=g(2x+1)=\frac{1}{2x+1}, x\not= -\frac{1}{2} \end{equation*}

and

\begin{equation*} (f\circ g)(x)=f(g(x))=f\left( \frac{1}{x}\right)=\frac{2}{x}+1, x\not= 0. \end{equation*}

Example 1.5.3. Sonoko.

Sonoko is a Ph.D. candidate in the Department of Mathematics at Dalhousie University, Halifax, NS. Recently, Sonoko's paper on the accessibility of the set of Fibonacci numbers was accepted in The Fibonacci Quarterly, the official publication of the Fibonacci Association. To celebrate this great news, Sonoko invited her roommate Janice for a dinner at Presto Panini Cafe, Sonoko's favourite Italian restaurant.

Sonoko ordered a bowl of penne pasta in pesto sauce for $\$15$ and Janice's choice was a bowl of gnocchi in gorgonzola sauce with spinach and toasted walnuts that costed $\$17\text{.}$ To celebrate this very special occasion two friends shared a piece of Presto Panini's famous tiramisu $(\$8)$ and a 1/2 litter of Chianti $(\$20)\text{.}$

In Nova Scotia sales taxes applied to foodservice are calculated as a single tax, called the Harmonized Sales Tax (HST), of $15\%$ of the total food and beverage purchase.

Since as an undergraduate student she used to work as a waitress, Sonoko is a very generous tipper. Her tipping policy is to give $8/5\text{,}$ the ratio of the sixth and the fifth terms of the Fibonacci sequence, of the HST amount to the server.

Questions:

What was the amount of the HST on Sonoko and Janice's bill?
What was the tip that Sonoko left for the server?
Suppose that $x$ is the amount in dollars of the total food and beverage purchase. Let $h(x)$ be the function that associates the amount of the HST to the amount $x\text{.}$ Find an expression for $h(x)\text{.}$
Let $\displaystyle f(t)=\frac{8}{5}\cdot t\text{.}$ Express Sonoko's tipping policy in terms of the functions $h$ and $f\text{.}$

Solution

Sonoko and Janice's bill before HST was

\begin{equation*} \$15+\$17+\$8+\$20=\$60. \end{equation*}

The amount of the HST was $0.15\cdot\$ 60= \$9\text{.}$
Sonoko calculated the tip as

\begin{equation*} \frac{8}{5}\cdot \$9=1.6\cdot \$9=\$14.40. \end{equation*}
Since the HST is calculated as $15\%$ of the total amount, the function $h$ is given as $h(x)=0.15x\text{.}$
Sonoko's tipping policy is the composition of the function $f$ and $h\text{:}$

\begin{equation*} s(x)=(f\circ h)(x)=f(h(x))=f(0.15x)=\frac{8}{5}\cdot 0.15x=0.24\cdot x. \end{equation*}

MUST KNOW - PREPARATION FOR CALCULUS: Decomposition of functions:

The process of breakdown of a function into less complex functions.

Figure 1.65. Decomposition of the *oreo function*

Example 1.5.4. Decomposition.

Express the given function as the composition of two or more functions:

$\displaystyle F(x)=(2x+1)^2$
$\displaystyle G(x)=3x^2+1$
$\displaystyle H(x)=3(2x+1)^2+1$

Solution

Notice that, to evaluate $F(x)$ for a given real number $x\text{,}$ we need first to evaluate the number $2x+1$ and then to square this number. Hence the “inside function” is $f(x)=2x+1$ and the “outside function” is $g(x)=x^2\text{.}$ It follows

\begin{equation*} (g\circ f)(x)=g(f(x))=g(2x+1)=(2x+1)^2=F(x). \end{equation*}
Notice that, to evaluate $G(x)$ for a given real number $x\text{,}$ we need first to evaluate the number $x^2$ and then to multiply this number by 2 and add 1. Hence the “inside function” is $f(x)=x^2$ and the `“outside function” is $g(x)=2x+1\text{.}$ It follows

\begin{equation*} (g\circ f)(x)=g(f(x))=g(x^2)=2x^2+1=G(x). \end{equation*}
Notice that, to evaluate $H(x)$ for a given real number $x\text{,}$ we need first to evaluate the number $2x+1\text{,}$ then to square it and finally to multiply by 3 and add 1. Hence if we take $f(x)=2x+1\text{,}$ $g(x)=x^2\text{,}$ and $h(x)=3x+1$ then we get

\begin{equation*} h(g(f(x)))=h(g(2x+1))=h((2x+1)^2)=3(2x+1)^2+1=H(x). \end{equation*}

Identity function: The identity function is the function $I$ defined by

\begin{equation*} I(x)=x \end{equation*}

for every real number $x\text{.}$ See Figure 1.66.

Figure 1.66. The identity function $I(x)=x$

Important observation: For any function $f\text{:}$

\begin{equation*} f\circ I=I\circ f=f. \end{equation*}

Building a bank of functions: Linear functions. A linear function is a function of the form

\begin{equation*} f(x)=mx+b \end{equation*}

where $m$ and $b$ are given numbers.

Example 1.5.5. Linear or not.

Which of the following functions is NOT linear:

$\displaystyle I(x)=x$
$\displaystyle f(x)=-2x+3$
$\displaystyle g(x)=x^2+1$
$\displaystyle h(x)=-1$

Solution

The function $g(x)=x^2+1$ is not linear, i.e. it is not in the form $y=mx+b$ for some real numbers $m$ and $b\text{.}$

Otherwise, $I(x)=x=1\cdot x+0\text{,}$ $f(x)=-2x+3\text{,}$ and $h(x)=-1=0\cdot x-1\text{.}$

For graphs of those four functions see Figure 1.67.

Figure 1.67. The graph of a linear function is a straight line

Example 1.5.6. Composition of two linear functions.

Prove that the composition of two linear functions a linear function.

Solution

Let $m,n,p$ and $q$ be real numbers and let $f(x)=mx+n$ and $g(x)=px+q$ be two linear functions.

By definition

\begin{equation*} (g\circ f)(x)=g(f(x))=g(mx+n)=p(mx+n)+q=pmx+pn+q=ax+b, \end{equation*}

where $a=pm$ and $b=pn+q\text{.}$

Making new from old: Let $f$ and $g$ be two real valued functions with the same domain $D$ and let $a$ and $b$ be two real numbers. We define functions $af+bg\text{,}$ $f\cdot g\text{,}$ and $\displaystyle \frac{f}{g}$ in the following way:

\begin{equation*} (af+bg)(x)=af(x)+bg(x) \end{equation*}

\begin{equation*} (f\cdot g)(x)=f(x)\cdot g(x) \end{equation*}

\begin{equation*} \left(\frac{f}{g}\right) (x)=\frac{f(x)}{g(x)} \text{ if }g(x)\not=0 \end{equation*}

Example 1.5.7. New from old.

Let $f(x)=2x+1$ and $g(x)=x-3\text{.}$ Evaluate:

$\displaystyle (f-g)(2)=$
$\displaystyle (f\cdot g)(2)=$
$\displaystyle \displaystyle \left(\frac{f}{g}\right)(3)=$

Solution

By definition $(f-g)(2)=f(2)-g(2)=5-(-1)=6\text{.}$
By definition $(f\cdot g)(2)=f(2)\cdot g(2)=5\cdot(-1)=-5\text{.}$
Note that $g(3)=3-3=0\text{.}$ Thus $\displaystyle \left(\frac{f}{g}\right)(3)$ is not defined.