Precalculus: Lecture Notes

1. Definition of a function.

Decide if the given rule is a function. If it is, find the value of the function if \(x=\) yourself. If the given rule is not a function, explain clearly which condition in the definition of a function is not satisfied.

1. Rule: Each student at SFU is associated with their SFU ID number.

2. Rule: Each student at SFU is associated with the course that she or he is currently taking.

3. Rule: Each student at SFU is associated with the car model that she or he owns.

4. Rule: Each student at SFU is associated with their birthday.

2. Definition of a function.

We define a function \(f\) in the following way: for every real number \(x\text{,}\) \(f(x)\) is the largest integer that is less than or equal to \(x\)

1. Find \(f(0)\text{,}\) \(f(0.5)\text{,}\) \(f(0.75)\text{,}\) \(f(1)\text{,}\) \(f(1.5)\text{,}\) \(f(1.75)\text{,}\) \(f(2)\text{.}\)

2. Find all solutions of the equation \(f(x)=1\text{.}\)

3. Sketch a graph of the function \(f\text{.}\)

3. Definition of a function.

Let \(f\) be the function which associates to an integer \(n\) the number \(\cos n\pi\) if \(n\) is even, and \(\sin n\pi\) if \(n\) is odd.

1. Complete the following table:

   \begin{equation*} \begin{array}{c||c|c|c|c|c|c} n\amp -4\amp -3\amp0\amp3\amp11\amp16\\ \hline f(n)\amp\amp\amp\amp\amp\amp\\ \end{array} \end{equation*}

2. Express the function \(f\) as a piecewise defined function.

3. State the domain and the range of the function \(f\text{.}\)

4. Draw a graph of \(f\text{.}\)

4. Composition of functions.

Sonoko is a Ph.D. candidate in the Department of Mathematics at Dalhousie University, Halifax, Nova Scotia. Recently her paper on the accessibility of the set of Fibonacci numbers was accepted in The Fibonacci Quarterly, the official publication of the Fibonacci Association. To celebrate this great news Sonoko invited her roommate Janice for a dinner at Presto Panini Cafe, Sonoko's favourite Italian restaurant.

Sonoko ordered a bowl of penne pasta in pesto sauce for \(\$15\) and Janice'c choice was a bowl of gnocchi in gorgonzola sauce with spinach and toasted walnuts that costed \(\$17\text{.}\) To celebrate this very special occasion the girls shared a piece of Presto Panini's famous tiramisu \((\$8)\) and a 1/2 litter of Chianti \((\$20)\text{.}\)

In Nova Scotia sales taxes applied to foodservice are calculated as a single tax, called the Harmonized Sales Tax (HST), of \(15\%\) of the total food and beverage purchase.

Since as an undergraduate student she used to work as a waitress, Sonoko is a very generous tipper. Her tipping policy is to give \(8/5\text{,}\) the ratio of the sixth and the fifth terms of the Fibonacci sequence, of the HST amount to the server.

1. What was the amount of the HST on Sonoko and Janice's bill?

2. What was the tip that Sonoko left for the server?

3. Suppose that \(x\) is the amount in dollars of the total food and beverage purchase. Let \(h(x)\) be the function that associates the amount of the HST to the amount \(x\text{.}\) Find an expression for \(h(x)\text{.}\)

4. Let \(f(t)=\frac{8}{5}\cdot t\text{.}\) Express Sonoko's tipping policy in terms of the functions \(h\) and \(f\text{.}\)

5. Composition and decomposition.

1. Let \(f(x)=2\sqrt{x}\text{,}\) \(g(x)=3^x\) and \(h(x)=\cos{x}\text{.}\)

   1. Find \(h\circ g\circ f\text{.}\) What is the domain of \(h\circ g\circ f\text{?}\)

   2. Find \(h\circ f\circ g\text{.}\) What is the domain of \(h\circ f\circ g\text{?}\)

2. Given \(F(x) = \sin (e^{x^2-x})\) find functions \(p\text{,}\) \(q\) and \(r\) such that \(F = p\circ q \circ r\text{.}\)

6. Composition.

Let \(f(x)=\frac{1}{x+1}\) and \(g(x)=\ln x\text{.}\) Find \(g\circ f\text{.}\) What is the domain of \(g\circ f\text{?}\) Find \(f\circ g\text{.}\) What is the domain of \(f\circ g\text{?}\)

7. Decomposition.

Given \(F(x) = \cos (e^{\sin \sqrt{x}})\) find functions \(p\text{,}\) \(q\text{,}\) \(r\text{,}\) and \(t\) such that \(F = p\circ q \circ r\circ t\text{.}\)

8. Line.

1. Find the number \(t\) such that the line containing the points \((-3,t)\) and \((2,-4)\) is parallel to the line containing the points \((5,6)\) and \((-2,4)\text{.}\)

2. Find an equation of the line that is perpendicular to the two lines in the first part of this question and passes through the point \((3,0)\text{.}\)

9. Power function.

Suppose that you are given an open top box with the square base. Let \(x\) be the length of the side of the base and let the volume of the box be \(V=1\text{.}\) Express the surface area of the box in terms of two power functions of \(x\text{.}\)

10. Quadratic function.

A hockey team plays in an arena that has a seating capacity of 15,000 spectators. With the ticket price set at \(\$50\text{,}\) average attendance at recent games has been \(10,500\text{.}\) A market survey indicates that for each dollar the ticket price is lowered, the average attendance increases by 100.

1. Find a function that models the revenue in terms of ticket price.

2. Which attendance will give the maximum revenue? Justify your answer.

11. Piecewise defined function.

Let \(f\) be an odd function defined on the interval \([-2,2]\) and such that

1. Complete the following table:

   \begin{equation*} \begin{array}{c||c|c|c|c|c|c|c|c|c} x\amp2\amp1.5\amp1\amp0.5\amp0\amp-0.5\amp-1\amp-1.5\amp-2\\ \hline f(x)\amp\amp\amp\amp\amp\amp\amp\amp\amp\\ \end{array} \end{equation*}

2. Draw the graph of the function\(f\text{.}\)

3. Draw the graph of the function \(g(x)=-2f(x-1)+1\text{.}\)

12. Distance formula.

A particle is moving along the the curve \(y = \sqrt{x}\) starting from the origin. What is the relationship between the \(x\) coordinate of the particle and the distance of the particle from the origin? For which \(x\) will the distance be equal to \(\sqrt{12}\text{?}\)

13. Distance formula.

A particle is moving along the curve \(y = \frac{1}{x}\text{,}\) \(x\gt 0\text{.}\)

1. What is the relationship between the \(x\) coordinate of the particle and the distance of the particle from the origin?

2. For which \(x\) will the distance be equal to \(\frac{\sqrt{17}}{2}\text{?}\)

14. Define and classify.

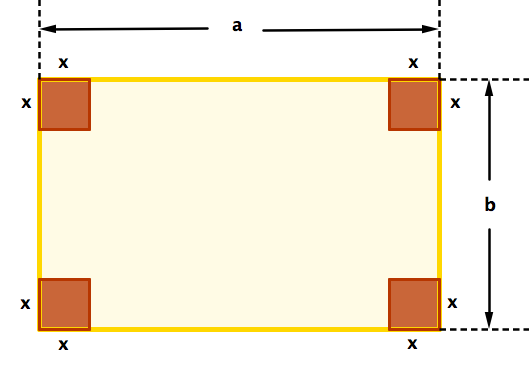
A rectangular sheet of cardboard measures \(a\) cm by \(b\) cm. Equal squares are cut out of each corner and the sides are turned up to form an open rectangular box.

Express the volume of the box in terms of \(x\text{,}\) the length of the side of the square. Classify the obtained function (i.e. determine if is this a linear function, a power function, a polynomial, an exponential or a logarithmic function.)

What is the domain of the function? Sketch the graph of the function under the assumption that \(0\lt b\lt a\text{.}\)

See Figure 5.1.

15. Distance and quadratic.

Find the point on the line \(2x+3y=1\) that is closest to the point \((1,-1)\text{.}\)

16. Rational function.

Let

1. Determine the domain of the function \(f\text{.}\)

2. Determine all vertical asymptotes.

3. Determine all zeros of the function \(f\text{.}\)

4. Find a function of the form \(g(x) = ax^n\text{,}\) where \(a\) is a real number and \(n\) is an integer, which describes the behaviour of \(f\) near \(\pm \infty\text{.}\)

5. Determine intervals where \(f(x)\gt 0\) and where \(f(x)\lt 0\text{.}\)

6. Sketch a graph of the function \(f\text{.}\)

17. Logarithms.

Using the approximations \(\log 2 \approx 0.301\) and \(\log 5 \approx 0.699\text{,}\) estimate each of the following to three decimal places. (You can check your answers with a calculator.)

1. Estimate \(\log 4\text{.}\)

2. Estimate \(\log 8\text{.}\)

3. Estimate \(\log 10\text{.}\)

4. Estimate \(\log 16\text{.}\)

5. Estimate \(\log 20\text{.}\)

6. Estimate \(\log 25\text{.}\)

7. Estimate \(\log 32\text{.}\)

8. Estimate \(\log 40\text{.}\)

9. Estimate \(\log 50\text{.}\)

10. Estimate \(\log 64\text{.}\)

11. Estimate \(\log 80\text{.}\)

12. Estimate \(\log 100\text{.}\)

13. Estimate \(\log 125\text{.}\)

14. Estimate \(\log 160\text{.}\)

15. Estimate \(\log 200\text{.}\)

16. Estimate \(\log 250\text{.}\)

18. Volume of a cone.

The volume of a cone is given by \(V =\frac{r^2 h\pi}{3}\text{.}\) Express the volume as a function of \(\theta\text{.}\) See Figure 5.2.

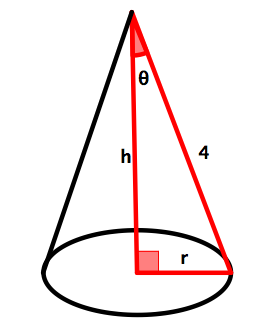
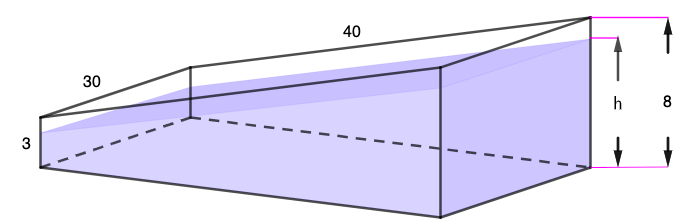
19. Define a function.

The swimming pool shown in the figure is \(3\)–ft deep at the shallow end, \(8\)–ft deep at the deepest end, \(40\)–ft long, \(30\)–ft wide, and the bottom is an inclined plane. Water is pumped into the pool. See Figure 5.3.

1. Express the volume of the water in the pool as a function of height \(h\) of the water measured from the bottom of the pool at the deep end. [Hint: The volume will be a piecewise-defined function.]

2. Determine the domain and range of the function found in part (a).

20. Define two functions.

Jayden has a rectangular yard that is 30ft by 34ft. He would like to add a sidewalk along the outside of two adjacent sides of the yard. The contractor quotes a price of \(\$20\) per square foot to put in the sidewalk.

1. Draw a picture of the situation that shows the yard and adjoining sidewalk.

2. If the sidewalk is only 1 ft wide, how many square feet of sidewalk would be have?

3. What is the cost of a 1 ft wide sidewalk?

4. Write a function \(A(x)\) for the area (the number of square feet) of sidewalk installed if the sidewalk is \(x\) ft wide.

5. Write a function \(C(x)\) for the cost of installing a sidewalk that is \(x\) ft wide.

6. Use the function \(C\) to find the cost of installing a sidewalk 2 ft wide.

7. If Jayden has \(\$4, 000\) to spend, what is the widest he can make the sidewalk to the nearest tenth of a foot?

21. Three functions.

Men's shoe size conversion is given by the following table

Let the set \(A\) be given by

Let functions \(f\text{,}\) \(g\text{,}\) and \(h\) be defined on the set \(A\) in the following way:

It is known that

1. Draw tables for the functions \(g\) and \(h\text{.}\)

2. Draw the graphs of the functions \(f\text{,}\) \(g\text{,}\) and \(h\) in the coordinate system in which the elements of the set \(A\) (in the alphabetical order) are represented as dots on the horizontal axis, and the vertical axis is a number line.

3. Explain carefully how the three graphs are related.

4. Based on your observation in part (b), express functions \(g\) and \(h\) in terms of the function \(f\text{.}\)

22. One–to–one function.

A function \(f:\left[-\frac{\pi}{2},\frac{\pi}{2}\right]\to [-1,1]\) is given by its graph. See Figure 5.4.

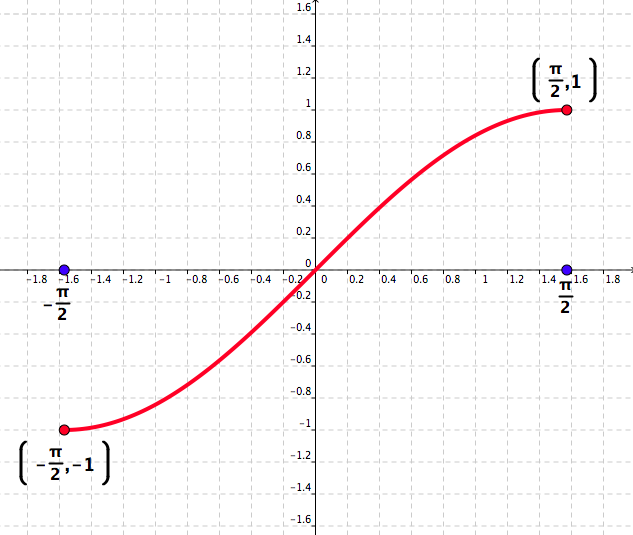
1. Use the horizontal line test to determine that the function \(f\) is one–to–one.

2. State the domain and range of the function \(f^{-1}\text{.}\)

3. Draw a graph of the function \(f^{-1}\text{.}\)

23. One–to–one function.

Let \(f\) be a function on the domain \([-10, 1]\) which is defined by

Is \(f\) a one–to–one function? Justify your answer.

24. Bernoulli polynomials.

The first several so–called Bernoulli polynomials are given as follows:

It is known that the Bernoulli polynomials satisfy the following relation:

Check this fact for \(n=1\text{,}\) \(n=2\text{,}\) and \(n=3\text{,}\) i.e. check that

1. \(\displaystyle B_1(x+1)-B_1(x)=1,\)

2. \(\displaystyle B_2(x+1)-B_2(x)=2x,\)

3. \(\displaystyle B_3(x+1)-B_3(x)=3x^2.\)

25. Euler polynomials.

The first few so–called Euler polynomials are given as follows:

It is known that the Euler polynomials satisfy the following property. If a real number \(h\) is such that \(|h|\) is very small then, for any real number \(x\text{,}\)

Check this fact for \(x=1\text{,}\) \(n=2\) and \(n=3\text{,}\) i.e. check that if \(|h|\) is small then:

1. \(\displaystyle \frac{E_2(1+h)-E_2(1)}{h}\approx 2E_{1}(1)\)

2. \(\displaystyle \frac{E_3(1+h)-E_3(1)}{h}\approx 3E_{2}(1).\)

26. Logarithmic function.

Let

1. Determine the domain of the function \(f\text{.}\)

2. Determine all zeros of the function \(f\text{.}\)

3. Determine the vertical asymptote.

4. Sketch a graph of the function \(f\text{.}\)

5. Solve the equation \(f(x)=21\text{.}\)

6. Find the inverse function \(f^{-1}\) of the function \(f\text{.}\)

27. Unit circle and angles.

Each point on the unit circle corresponds to a unique angle \(\alpha\) having the positive part of the \(x\)–axis as its initial ray and such that \(0\leq \alpha \lt 2\pi\) (in radians.)

Complete the following table:

28. Trigonometric identiies.

Assuming all terms are defined, simplify

29. Powers of \(-1\).

Let \(f\) be the function which associates to an integer \(n\) the number 1 if \(n\) is even, and \(-1\) if \(n\) is odd. Find the following: \(f(2), f(3), f(145), f(-5), f(0)\text{.}\)

Can you find a formula for \(f\text{?}\)

30. Function and its meaning.

The number of gallons of paint needed to paint a house depends on the size of the house. A gallon of paint typically covers \(250~ \text{ft}^2\text{.}\) Thus the number of gallons of paint, \(n\text{,}\) is a function of the area to be painted, \(A~ \text{ft}^2\text{.}\) We write \(n=f(A)\text{.}\)

1. Find a formula for \(f\text{.}\)

2. Explain in words what the statement \(f(10,000)=40\) tells us about painting houses.

31. Building, wall, and ladder.

A \(10\)–ft wall stands \(5\) ft from a building and a ladder of variable length \(L\text{,}\) supported by the wall, is placed so it reaches from the ground to the building. Let \(y\) denote the vertical distance from the ground to where the tip of the ladder touches the building, and let \(x\) denote the horizontal distance from the wall to the base of the ladder.

See Figure 5.5.

1. Find an expression for the height \(y\) as a function of \(x\text{.}\)

2. Find an expression for the length \(L\) as a function of \(x\text{.}\)

3. Determine the domain and range of the function \(L(x)\) found in part (b).

32. Rancher, plot, and fance.

A rancher intends to work off a rectangular plot of land that will have an area of \(1000 \textrm{m}^2\text{.}\) The plot will be fenced and divided into two equal portions by and additional fence parallel to two sides. See Figure 5.6.

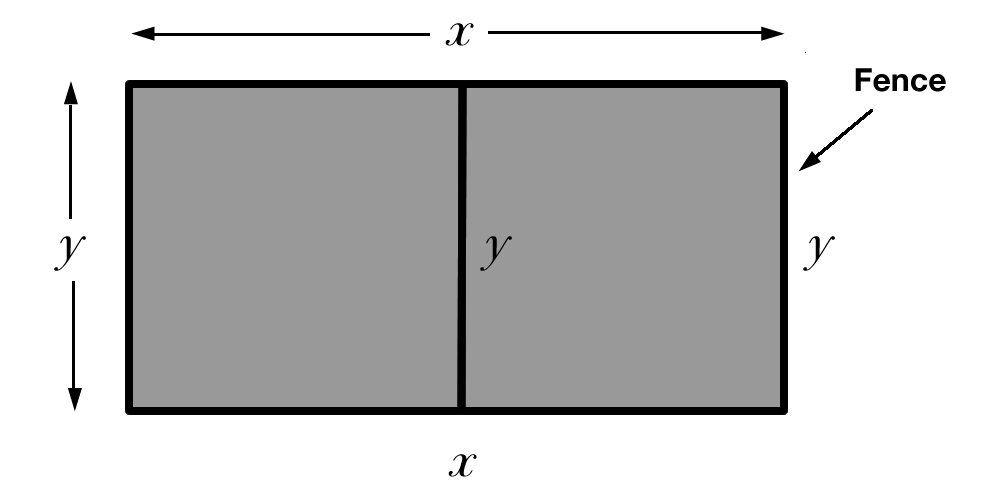
1. Find the total length of fence used as a function of \(y\text{.}\)

2. What is the domain of the function found in part (a)?

33. Define a function.

An airplane is flying parallel to the ground at an altitude of 3 km. It flies directly over an observer on the ground and continues flying parallel to the ground.

Let \(d\) be the distance from the observer to the airplane.

1. Draw a picture that represents the situation.

2. Identify and label all constants and variable quantities.

3. Find a relationship between d and the other variable quantities; express this relationship as an equation.

34. Distance between two cars.

Two cars leave an intersection at the same time. One car travels north at the speed of 60 km/h and the other travels west at the speed of \(50\) km/h. Let \(t\) be time in hours since the cars left the intersection. Let \(d\) be the distance between the two cars at time \(t\text{.}\)

1. Draw a picture that represents the situation.

2. Express \(d\)as a function of \(t\text{.}\)

35. Graphs.

The graph of a function \(f\) is defined to be the set of all points \((x,y)\)in the Cartesian plane satisfying the equation \(y=f(x)\text{.}\) Sketch the graphs of the following functions.

1. \(\displaystyle f(x) = x+1\)

2. \(\displaystyle g(x) = x^2 -1\)

3. \(\displaystyle h(x) = \frac{x^2-1}{x-1}\)

4. \(\displaystyle i(x) = \begin{cases} 2x+3 \amp \text{ if } x\le 0 \\ x^2+3 \amp \text{ if } x\gt 0 \end{cases}\)

5. \(\displaystyle j(x) = |x|\)

6. \(\displaystyle k(x) = 2^{-x}\)

7. \(\displaystyle l(x) = \log_{\frac{1}{2}}x\)

8. \(\displaystyle m(x)=\sin x\)

9. \(\displaystyle n(x)=\cos x\)

10. \(\displaystyle o(x)=\tan x\)

11. \(\displaystyle p(x)=x^3\)

12. \(\displaystyle q(x)=\frac{1}{x}\)

13. \(\displaystyle r(x)=e^x\)

14. \(\displaystyle s(x)=\ln x\)

36. Angles.

Sketch the following angles in standard position and give the measure of the angle in degrees:

1. \(\displaystyle \frac{\pi}{2}\)

2. \(\displaystyle \frac{\pi}{4}\)

3. \(\displaystyle -\frac{5\pi}{6}\)

4. \(\displaystyle \frac{13\pi}{3}\)

37. Transformations.

SeeFigure 5.7 for the graph of \(f\text{.}\) Sketch the graph of of the function \(x\mapsto \frac{1}{2}(f(x-4)-8)\text{.}\)

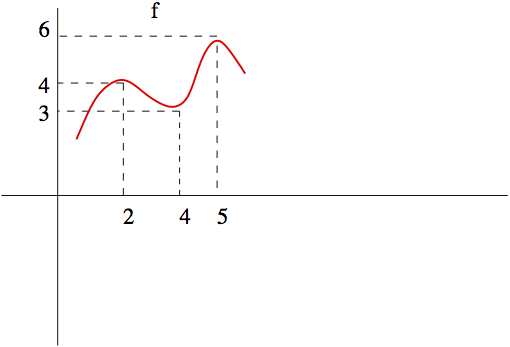
38. New functions.

If \(f(-1)=1\text{,}\) \(f(2)=3\text{,}\) \(g(-1)=-5\) and \(g(2)=17\) find \((f+g)(-1)\text{,}\) \((fg)(-1)\) and \((f/g)(2)\text{.}\)

39. Transformations.

SeeFigure 5.8 for the graph of \(f\text{.}\) Sketch the graph of of the function \(x\mapsto g(x)=2-\frac{1}{2}\cdot f(x-2)\text{.}\)

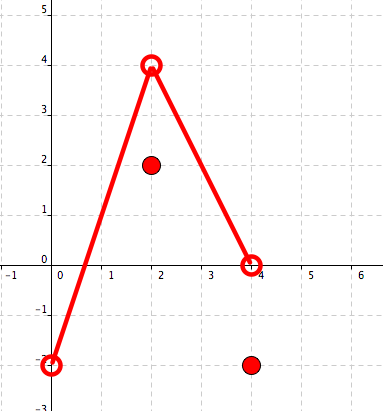
40. Composition and decomposition.

1. If \(f(x)=2^x\text{,}\) \(g(t)=3\sqrt{t}\) and \(h(\theta)=\sin{\theta}\) find \(h\circ f\circ g\text{.}\) What is the domain of \(h\circ f\circ g\text{?}\)

2. Given \(F(x) = (1+2\sin{x})^3\) find function \(p\text{,}\) \(q\) and \(r\) such that \(F = p\circ q \circ r\text{.}\)

3. Write \(\sin^2{(e^{x^2-x})}\) as a composition of (elementary) functions.

41. Taste of calculus.

For each of the following functions draw its graph and determine intervals where the function is monotone, i.e. where the function increases and where the function decreases.

Also, for each of the given functions in parts (a)–(d) find and simplify, if possible, the ratio

where \(F\) represents the appropriate function.

If the function is one-to-one draw the graph of its inverse function.

1. \(\displaystyle f(x)=x^2\)

2. \(\displaystyle g(x)=x^3\)

3. \(\displaystyle h(x)=e^x\)

4. \(\displaystyle i(x)=\sin x\)

5. \(j(x)=\sin x\text{,}\) \(x\in \left[ -\frac{\pi}{2},\frac{\pi }{2}\right]\)

42. Inverse functions.

Find a formula for the inverse of:

1. \(\displaystyle \displaystyle f(x)=\frac{x}{3x+1}\)

2. \(\displaystyle g(x)=e^{x^3+1}-2\)

3. \(\displaystyle h(x)=4(\log (x+2))^3 +1\)

4. \(\displaystyle k(x)=\displaystyle \frac{2+e^x}{1-3e^x}.\)

43. Logarithms.

1. Determine \(\log_2{(16)}\text{,}\) \(\log_2{(\frac{1}{8})}\) and \(\log_2{(1)}\text{.}\)

2. Can you find \(\log_2{(-32)}\text{?}\) Explain your reasoning.

44. Exponential equation.

Solve the equation \(e^{x^3-3}-9 = 0\) for \(x\text{.}\)

45. Exponential equation.

For any \(-1\le x \le 1\) and any \(-\frac{\pi}{2}\le y \le\frac{\pi}{2}\) we define the function \(\sin^{-1}: [-1,1]\to \left[ -\frac{\pi}{2},\frac{\pi}{2}\right]\) by

Determine the following:

1. \(\displaystyle \sin^{-1}\left(\frac{\sqrt{3}}{2}\right)\)

2. \(\displaystyle \displaystyle \sin\left(\sin^{-1}\left(\frac{1}{3}\right)\right)\)

3. \(\displaystyle \sin^{-1}\left(\sin\left(\frac{3\pi}{4}\right)\right)\)

46. True or False.

Justify your answers.

1. If \(f(s)=f(t)\) then \(s=t\text{.}\)

2. If \(\) is an odd function and \(f(3)=6\)then \(f(-3)=-6\text{.}\)

3. If \(x_1\lt x_2\) and \(g\) is a decreasing function then \(g(x_1)\gt g(x_2)\text{.}\)

4. If \(f\) and \(g\) are functions then \(f\circ g= g\circ f\text{.}\)

5. If the line \(x=1\) is a vertical asymptote of \(y=f(x)\text{,}\) then \(f\) is not defined at \(1\text{.}\)

6. The graph of a function can have only one \(y\)–intercept.

7. Two lines with negative slopes could be perpendicular.

47. Simplify.

Give the domain and a simplified expression for:

1. \(\displaystyle m(h) = \frac{\sqrt{9+h} - 3}{h}\)

2. \(h(x) = \frac{|3-6x|}{2x-1}\text{.}\) Sketch the graph of \(h\text{.}\)

48. Average rate of change.

The average rate of change of a function \(f\) over the interval \([x_1,x_2]\) is defined as

Notice that this can be interpreted as the slope of the secant line through the points \((x_1,f(x_1))\) and \((x_2,f(x_2))\text{.}\)

If a cylindrical tank holds \(100,000\) gallons of water, which can be drained from the bottom of the tank in an hour, then Torricelli's Law gives the volume \(V\) of water remaining in the tank after \(t\) minutes as

Find the average rate at which the water is flowing out of the tank between:

1. \(0\) and \(10\) minutes,

2. \(40\) and \(50\) minutes.

What is the average rate at which the water is flowing out of the tank over the entire \(60\) minute time period?

49. Lamppost..

A \(6\)–ft tall man walks away from a \(15\)–ft lamppost and the man's shadow is cast on the ground.

1. Draw a picture to represent this situation, and identify and label all constants and variables.

2. Determine the relationship between the distance \(x\) from the man to the lamppost and length of the man's shadow.

50. Logarithms.

Let \(s\) and \(t\) be real numbers such that \(\log _2s=3/2\) and \(\log_2t=4/3\text{.}\)

1. Calculate \(\log_2(s^2t^3)\text{.}\)

2. Calculate \(\log_4((st)^5)\text{.}\)

3. Calculate \(\log_2\frac{s}{t}\text{.}\)

4. Calculate \(\frac{2^{s/2}-s}{s}\text{.}\)

5. Find all solutions to the equation \(s^x=t\text{.}\)

51. Various equations.

Find all solutions to the equation:

1. \(x^4-2x^2-1=0\text{.}\)

2. \(x^4-x^2-12=0\text{.}\)

3. \(2^{2x}-7\cdot 2^x-8=0\text{.}\)

4. \(4^{x+1}=3\text{.}\)

5. \(\frac{\log(12x)}{\log(4x)}=2\text{.}\)

6. \(\ln (x-1)-\ln x=\ln 3\text{.}\)

7. \(\log_3(\log_2x)=1\text{.}\)

8. \(1+\sin x=2\cos^2x\) for values of \(x\) in the interval \((-\pi,\pi ]\text{.}\)

9. \(\sin x+\cos x=1\) for values of \(x\) in the interval \((-\pi,\pi ]\text{.}\)

10. \(\sin 2x-\sin x=0\) for values of \(x\) in the interval \((-\pi,\pi ]\text{.}\)

11. \(3\sin ^4x-6\sin^2x+3=0\) or values of \(x\) in the interval \((-\pi,\pi ]\text{.}\)

52. Circle.

Find the radius and the centre of the circle \(x^2+6x+y^2-2y=0\text{.}\)

53. Investment.

Find the amount that should be invested now at the annual interest rate of \(4\%\) compounded quarterly, in order to be worth \(\$ 100,000\) in 10 years.

54. Trigonometric identities.

Use the identities

to:

1. To obtain the following identities:

   1. \(\sin (2x)=2\sin x\cos x\text{.}\)

   2. \(\cos (2x)= \cos^2x-\sin^2x=2(\cos^2x-1=1-2\sin^2x\text{.}\)

   3. \(\sin^2x=\frac{1-\cos 2x}{2}\text{.}\)

   4. \(\cos^2x=\frac{1+\cos 2x}{2}\text{;}\)

2. To determine the exact values in each of the following:

   1. \(\sin \frac{\pi}{12}\text{.}\)

   2. \(\cos \frac{7\pi}{12}\text{.}\)

   3. \(\tan \frac{\pi}{12}\text{.}\)

   4. \(\sin \frac{7\pi}{8}\text{,}\) \(\cos \frac{7\pi}{8}\text{,}\) and \(\tan \frac{7\pi}{8}\text{.}\)

55. Tangent line.

A tangent line to a circle at a point \(P\) on the circle is perpendicular to the line through \(P\) and the centre of the circle. See Figure 5.9.

1. Find the equation of the circle in the diagram.

2. Find the coordinates of the point \(P\text{.}\)

3. Find the equation of the line through \(P\) and the centre of the circle.

4. Find the equation of the line \(L\text{.}\)

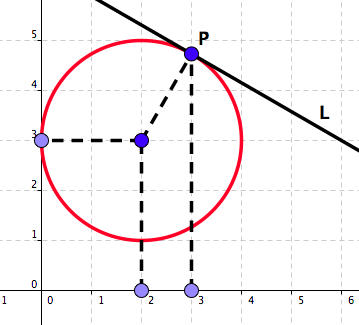
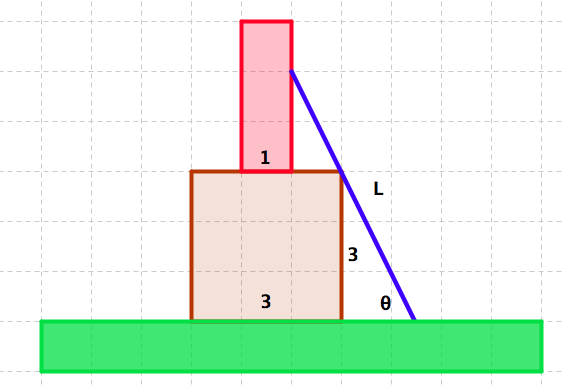
56. Post.

Consider a vertical post with a square cross–section of 1m by 1m set squarely on a cubical block 3m on a side. Supports from the floor to the sides of the post are desired. Find the relationship between the length of support \(L\) and the angle, \(\theta\text{,}\) the support makes with the floor. See Figure 5.10.

57. Law of Sines.

Pam and Brian are standing 8m apart from each other, trying to read a sign which is some distance away from both of them.

The angle formed by Pam's line of vision to the sign and her line of vision to Brian is \(\frac{\pi}{3}\text{.}\)

The angle formed by Brian's line of vision to the sign and his line of vision to Pam is \(\frac{\pi}{6}\text{.}\)

Find the distance between Pam and the sign.

58. Area.

Find the area of a regular octagon whose vertices are eight equally spaced points on the unit circle.

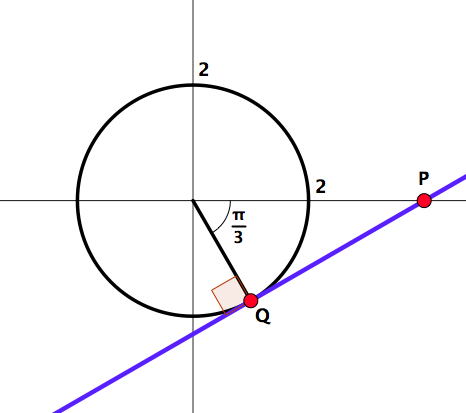
59. Tangent line.

This question is based on Figure 5.11.

1. Find the coordinates of the point \(Q\text{.}\)

2. Find the equation of the line through \(P\) and \(Q\text{.}\)

3. Find the equation of the line through \(P\) and the centre of the circle.

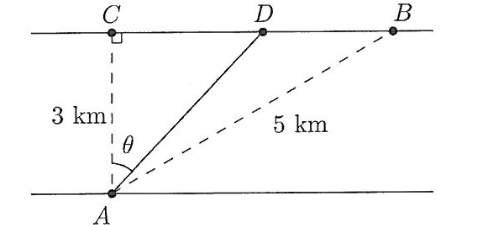
60. Find a function.

Ryan starts at point \(A\) located at the south bank of a river and wishes to reach point \(B\) located on the north bank of river. See Figure 5.12.

After some calculations, Ryan finds that a faster way to get to his destination is to use a boat to get from \(A\) to \(D\) and then walk the rest of the way from \(D\) to \(B\text{.}\)

The direct distance between \(A\) and \(B\) is 5 kilometres and the river is 3 kilometres wide. If Ryan's boat makes an angle of \(\theta\) with the dashed line connecting the points \(A\) and \(C\text{,}\) write down an expression, in terms of \(\theta\text{,}\) that describes the total distance Ryan must travel in this journey; i.e. the distance from \(A\) to \(D\) together with the distance from \(D\) to \(B\text{.}\)

Hint: What is the distance from \(C\) to \(B\text{?}\)

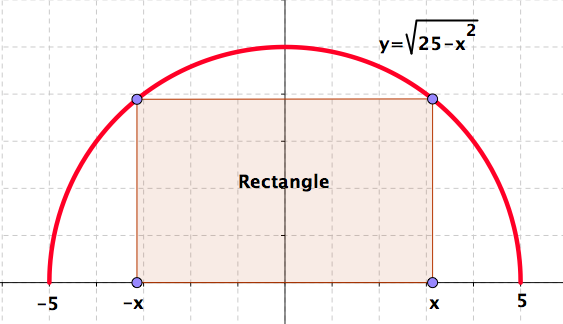
61. Rectangle.

A rectangle has two vertices on the \(x\)–axes and two vertices on the semicircle whose equation is \(y=\sqrt{25-x^2}\text{.}\) See Figure 5.13.

Find the area \(A\) of the rectangle as a function of \(x\text{.}\)

What is the domain of the function \(A=A(x)\) that you have obtain?

What can you tell about about the values of the function \(A(x)\) if \(x\) is close to 0? Close to 5?

62. Find a function.

Sketch the graph of a function \(f\) satisfying the following criteria:

1. The domain of \(f\) is \((-4,\infty)\)

2. The range of \(f\) is \((-\infty,5)\text{.}\)

3. \(f\) is increasing on the interval \((-4,-1)\) and on the interval \((2,\infty)\text{.}\)

4. The line \(x=-4\) is a vertical asymptote to the graph of \(f\text{.}\)

5. The line \(x=-3\) is a horizontal asymptote to the graph of \(f\text{.}\)

6. \(f(0)=1\text{.}\)