The Number $e$ and Natural Logarithm

Section 3.4 The Number $e$ and Natural Logarithm

One of the first conditions of happiness is that the link between Man and Nature shall not be broken. — Lev Nikolayevich Tolstoy, Russian writer, 1828 – 1910

🔗

Question: What is the most beautiful mathematical expression?

🔗

See Figure 3.10.

🔗

Number $e\text{.}$

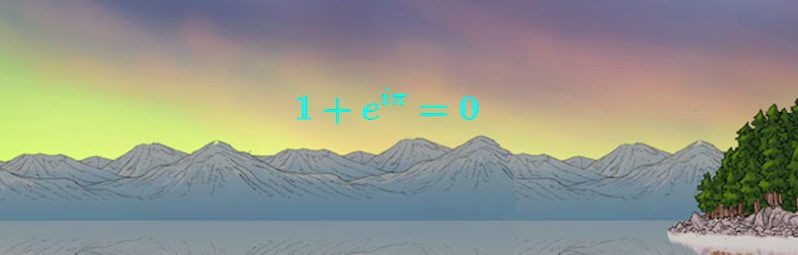
$\displaystyle e\approx 2.71828182845904523536028747135266249775724709369995\ldots$
First time mentioned in 1618 by (almost certainly) William Oughtred, 1574 – 1660.
The notation $e$ made its first appearance in a letter written by Leonhard Euler (1707 – 1783) in 1731.
What is $e\text{?}$

$\begin{equation*} \text{If }x\to 0\text{ then } (1+x)^{\frac{1}{x}}\to e. \end{equation*}$
Where is $e\text{:}$ See Figure 3.11.

FigureThe function $f(x)=e^x$ is the exponential function with the property that the slope of its tangent line at the point $(1,0)$ equals to 1.
Why $e\text{?}$ The number $e$ plays a role in your everyday life.

See Figure 3.12.

Figure 3.12. The compound interest formula and the continuous compound interest formula

🔗

Natural logarithm: The inverse function of the function

$f(x)=e^x$ is the function

$f^{-1}(x)=\log_ex\text{.}$

🔗

We write

$\begin{equation*} \log_e(x)=\ln (x), x>0. \end{equation*}$

🔗

We say that, for

$x>0\text{,}$

$\ln x$ is the \textbf{natural logarithm of }

$x\text{.}$

🔗

See Figure 3.13.

🔗

Figure 3.13. The function

$f(x)=e^x$ its inverse function

$f^{-1}(x)=\ln (x)\text{,}$ and the line

$y=x\text{.}$

🔗

Summary:

$\begin{equation*} \begin{array}{l|l|l} \amp f(x)=e^x\amp f^{-1}(x)=\ln (x)\\ \hline \text{Domain}\amp\mathbb{R}\amp(0,\infty)\\ \hline \text{Range} \amp (0,\infty)\amp \mathbb{R}\\ \hline \text{output}=0 \amp \text{Never}\amp x=1\\ \hline \text{output}=1 \amp x=0\amp x=e\\ \hline \text{Increasing}\amp \mathbb{R}\amp (0,\infty)\\ \hline \text{Decreasing}\amp \text{Never}\amp \text{Never}\\ \hline \text{One-to-one}\amp \text{Yes}\amp \text{Yes}\\ \hline \text{Inverse}\amp \ln x\amp e^x\\ \hline \text{Odd or even}\amp \text{Neither}\amp \text{Neither}\\ \hline \text{Vertical Asymptote}\amp --\amp x=0\\ \hline \text{Horizontal Asymptote}\amp y=0\amp --\\ \end{array} \end{equation*}$

🔗

All you need to know. If

$x\gt 0$ then

$\begin{equation*} \ln (x) =y \Leftrightarrow x=e^y. \end{equation*}$

🔗

Example 3.4.1. Logarithmic equations.

Solve the equation:

$\displaystyle \ln (x+1)=2,$
$\ln (x+12)-\ln(x+2)=\ln (x)\text{,}$
$\displaystyle \displaystyle \frac{\ln (x^2+12)}{\ln(x+2)}=2.$

Solution

Observe that the domain of the given equation is the set $\{x\in \mathbb{R}:x+1\gt 0\}=(-1,\infty)\text{.}$

By definition, for $x\in (-1,\infty)\text{,}$

\begin{equation*} \ln (x+1)=2\Leftrightarrow x+1=e^2\Leftrightarrow x=e^2-1. \end{equation*}
Observe that the domain of the given equation is given by

\begin{equation*} D=\{x:x+12\gt 0, \ x+2\gt 0,\text{ and }x\gt 0\} \end{equation*}

\begin{equation*} =\{x:x\gt -12, \ x\gt -2,\text{ and }x\gt 0\}=\{x:x\gt 0\}=(0,\infty). \end{equation*}

If follows that, for all $x\gt 0\text{,}$

\begin{equation*} \ln (x+12)-\ln(x+2)=\ln (x)\Leftrightarrow \ln\left(\frac{x+12}{x+2}\right)=\ln (x). \end{equation*}

Since the function $f(x)=\ln (x)$ is one–to–one, we have that, for all $x\gt 0\text{,}$

\begin{equation*} \ln\left(\frac{x+12}{x+2}\right)=\ln (x)\Leftrightarrow \frac{x+12}{x+2}=x\Leftrightarrow x+12=x^2+2x\Leftrightarrow x^2+x-12=0. \end{equation*}

The quadratic equation $x^2+x-12=0$ has two solutions, $x=-4$ and $x=3\text{.}$

We eliminate $x=-4$ since it is not in the domain of the given equation.

Hence $x=3$ is the only solution of the given equation.
Observe that the domain of the given equation is given by

\begin{equation*} D=\{x:x^2+12>0, \ x+2>0,\text{ and }\ln (x+2)\not= 0\}=\{x:x>-2,\text{ and }x+2\not=1\} \end{equation*}

\begin{equation*} =\{x:x>-2,\text{ and }x\not=-1\}=(-2,-1)\cup (-1,\infty). \end{equation*}

If follows that, for all $x\in D\text{,}$

\begin{equation*} \frac{\ln (x^2+12)}{\ln(x+2)}=2\Leftrightarrow \ln (x^2+12)=2\ln (x+2) \end{equation*}

\begin{equation*} \Rightarrow \ln (x^2+12)=\ln (x+2)^2\Leftrightarrow \ln (x^2+12)=\ln (x^2+4x+4). \end{equation*}

Since the function $f(x)=\ln (x)$ is one–to–one, we have that, for all $x\in D\text{,}$

\begin{equation*} \frac{\ln (x^2+12)}{\ln(x+2)}=2\Rightarrow x^2+12=x^2+4x+4\Leftrightarrow 4x=8\Leftrightarrow x=2. \end{equation*}

Clearly, $2\in D$ and we conclude that $x=2$ is the solution of the given equation.

🔗

Reminder: From the fact that the functions

$f(x)=e^x$ and

$g(x)=\ln (x)$ are inverse to each other it follows that:

$\begin{equation*} \ln \left(e^x\right)=x, x\in \mathbb{R} \end{equation*}$

🔗

and

$\begin{equation*} e^{\ln (x)}=x, x>0. \end{equation*}$

🔗

Example 3.4.2. The meaning of $x^x$ .

What is the meaning of the expression $\displaystyle x^x\text{,}$ $x\gt 0\text{?}$
Evaluate: $\displaystyle \pi^\pi$

Solution

By definition, for $x\gt 0\text{,}$

\begin{equation*} x^x=e^{x\ln (x)}. \end{equation*}

We justify this definition by observing the following.

Say that $x\gt 0$ and recall that, for $x\gt 0\text{,}$ $\displaystyle x=e^{\ln (x)}\text{.}$ Then

\begin{equation*} e^{x\ln (x)}=\left( e^{\ln (x)}\right)^x=x^x. \end{equation*}
By definition,

\begin{equation*} \pi ^\pi=e^{\pi\ln\pi}\approx 36.46215965. \end{equation*}

Section 3.4 The Number ee and Natural Logarithm

Example 3.4.1. Logarithmic equations.

Example 3.4.2. The meaning of xxx^x.

Section 3.4 The Number $e$ and Natural Logarithm

Example 3.4.2. The meaning of $x^x$ .