Section 5.2 Midterms
Subsection 5.2.1 Midterm 1
Problem 5.2.1.
[6 marks] In mathematics and computer science, the ceiling function f(x)=⌈x⌉ is defined in the following way:
for every real number x, f(x)=⌈x⌉ is the smallest integer that is greater than or equal to x.
-
Complete the following table:
x00.50.7511.51.7522.5f(x) Find all solutions of the equation f(x)=1.
Sketch a graph of the function f.
-
By definition of the function \(f(x) = \lceil x \rceil\text{:}\)
\begin{equation*} \begin{array}{c||c|c|c|c|c|c|c|c} \amp x\amp0\amp0.5\amp0.75\amp1\amp1.5\amp1.75\amp2\amp2.5\\ \hline f(x)\amp0\amp1\amp1\amp1\amp2\amp2\amp2\amp3\\ \end{array} \end{equation*} -
We need to find all real numbers \(x\) with the property that \(f(x) = \lceil x \rceil =1\text{.}\) In other words, we are looking for all real numbers such that the number 1 is the smallest integer that is greater than or equal to \(x\text{.}\)
This gives the set
\begin{equation*} \{x:0\lt x\leq 1\}=(0,1]. \end{equation*} -
See Figure 5.14.
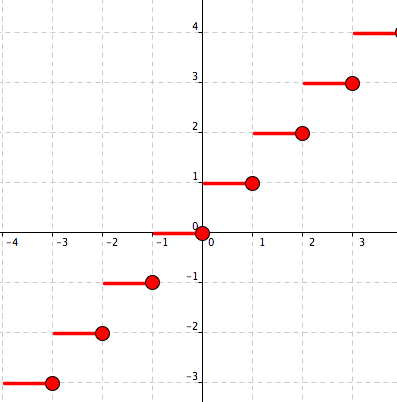
Figure 5.14. \(f(x) = \lceil x \rceil\)
Problem 5.2.2.
[6 marks]
-
Use the vertical line test to determine which curve represents a graph of a function. See Figure 5.15 and Figure 5.16.
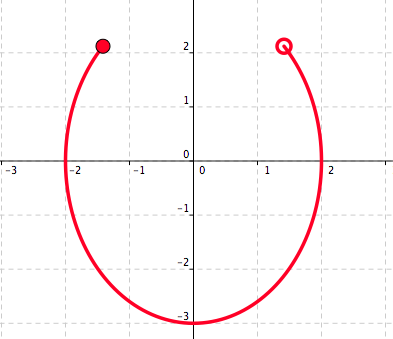
Figure 5.15. Curve A 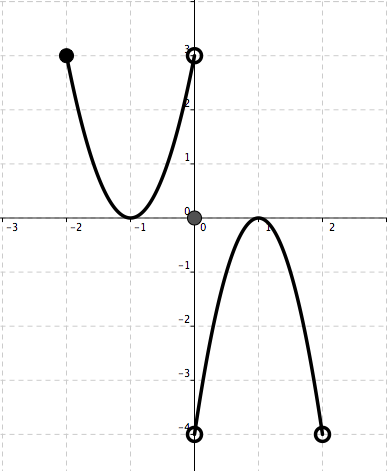
Figure 5.16. Curve B Circle the correct answer:
FunctionNot a functionA BA B -
Let f be the function you picked in the first part of this question.
Find the domain and the range of f.
-
Complete the following table:
x−2−103f(x) Estimate f(−0.75) and f(1.99999).
How many solutions does the equation f(x)=0 have? Find all solutions of this equation.
-
We note that there is a vertical line that intersects Curve A at two points. See Figure 5.17.
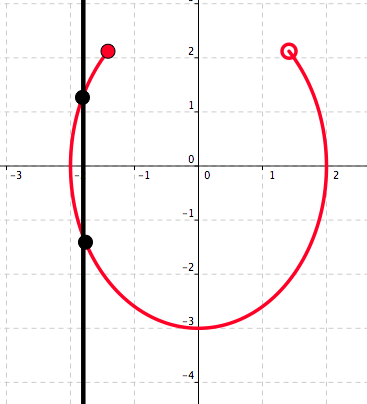
Figure 5.17. Curve \(A\) 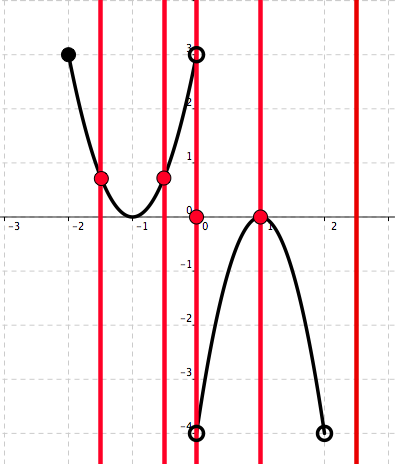
Figure 5.18. Curve \(B\) This means, by the vertical line test, that Curve A does not represent a graph of a function. We see from Figure 5.18 that every vertical line intersects Curve B in at most one point. Hence, Curve B represents a graph of a function. Therefore:
\begin{equation*} \begin{array}{c||c} \text{Function}\amp \text{Not a function} \\ \hline B\amp A \ \ \ \\ \end{array} \end{equation*} From the graph of \(f\) (Curve \(B\)) we read that the function \(f\) is defined on the interval \([-2,2)\text{.}\) The range of the function is the interval \((-4,3]\text{.}\)
-
We read from the graph:
\begin{equation*} \begin{array}{c||c|c|c|c} x\amp -2\amp -1\amp 0\amp 3\\ \hline f(x)\amp 3\amp 0\amp 0\amp\text{Not defined}\\ \end{array} \end{equation*} Based on the graph it appears that \(f(-0.75)\approx 0.75\) and \(f(1.99999)\approx -4\text{.}\)
From the graph we read that the equation \(f(x)=0\) has three solutions: \(-1\text{,}\) \(0\text{,}\) and \(1\text{.}\)
Problem 5.2.3.
[6 marks] Let f be an odd function defined on the interval [−2,2] and such that
-
Complete the following table:
x21.510.50−0.5−1−1.5−2f(x) Draw the graph of the function f.
Draw the graph of the function g(x)=−2f(x−1)+1.
-
To complete the table we use the given definition of the function \(f\) for \(x\in [0,2]\) and the fact that for odd functions we have \(f(-x)=-f(x)\) for all \(x\) in the domain of \(f\text{.}\) For example, since, from the above definition, \(f(2)=2\text{,}\) it follows that \(f(-2)=-f(2)=-2\text{.}\)
\begin{equation*} \begin{array}{c||c|c|c|c|c|c|c|c|c} x\amp2\amp1.5\amp1\amp0.5\amp0\amp-0.5\amp-1\amp-1.5\amp-2\\ \hline f(x)\amp2\amp2\amp1\amp0.5\amp0\amp-0.5\amp-1\amp-2\amp-2\\ \end{array} \end{equation*} -
First we draw the graph of \(f\) for \(x\in [0,2]\) according to the given definition. Then we use the fact that \(f\)is an odd function and that its graph must be symmetric with the respect to the origin. See Figure 5.19.
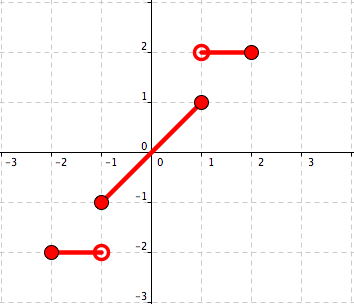
Figure 5.19. Graph of \(f\text{.}\) -
See Figure 5.20 – Figure 5.23.
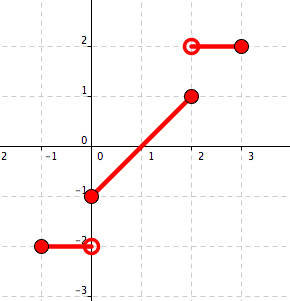
Figure 5.20. Horizontal shift to the right by 1. 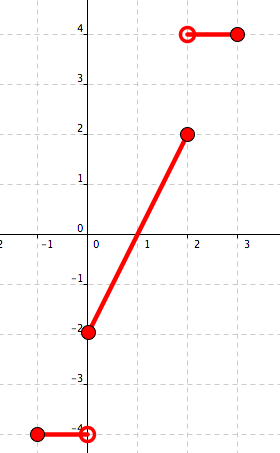
Figure 5.21. Vertical stretch by factor 2. 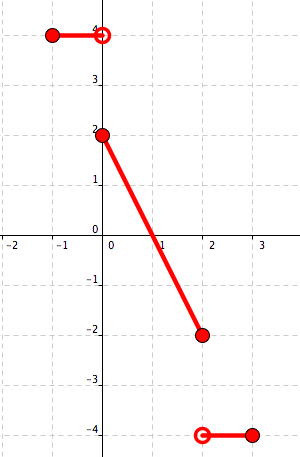
Figure 5.22. Reflection about the \(x\)–axis 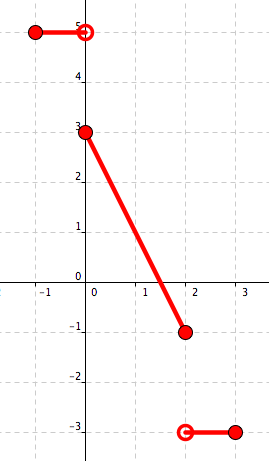
Figure 5.23. Vertical shift up by 1.
Problem 5.2.4.
[6 marks]
-
Let f(x)=x+1x and g(x)=x+1x−1.
Find an expression for the function (f∘g)(x) and determine its domain.
Find an expression for the function (g∘f)(x) and determine its domain.
Is it true that g∘f=f∘g? Justify your answer!
Decompose the function F(x)=3|x2−1|−2, i.e. find functions h, i, and j such that F=j∘i∘h.
-
Note that the function \(g\) is not defined for \(x=1\text{.}\) It follows that for all \(x\not= 1\text{:}\)
\begin{equation*} \begin{array}{rcl} (f\circ g)(x)\amp=\amp f(g(x))=f\left( \frac{x+1}{x-1}\right)\\ \amp=\amp \frac{x+1}{x-1}+\frac{1}{\frac{x+1}{x-1}}=\frac{x+1}{x-1}+\frac{x-1}{x+1}\\ \amp=\amp \frac{(x+1)^2+(x-1)^2}{(x+1)(x-1)}=\frac{x^2+2x+1+x^2-2x+1}{x^2-1}\\ \amp=\amp \frac{2x^2+2}{x^2-1}=\frac{2(x^2+1)}{x^2-1}.\\ \end{array} \end{equation*}Hence the domain of the function \(f\circ g\) is the set \(\{x:x\not= 1 \text{ and }x^2-1\not=0\}=\{x:x\not= 1 \text{ and }(x+1)(x-1)\not=0\}=\{ x: x\not= 1, x\not= -1\}\text{.}\)
-
Note that the function \(f\) is not defined for \(x=0\text{.}\) It follows that for all \(x\not= 0\text{:}\)
\begin{equation*} \begin{array}{rcl} (g\circ f)(x)\amp =\amp g(f(x))=g\left( x+\frac{1}{x}\right)\\ \amp =\amp \frac{x+\frac{1}{x}+1}{x+\frac{1}{x}-1}=\frac{\frac{x^2+1+x}{x}}{\frac{x^2+1-x}{x}}\\ \amp =\amp \frac{x^2+x+1}{x^2-x+1}\\ \end{array} \end{equation*}We observe that, for all real numbers \(x\text{,}\)
\begin{equation*} x^2-x+1=x^2-2\cdot \frac{1}{2}\cdot x+\frac{1}{4}+\frac{3}{4}=\left( x-\frac{1}{2}\right)^2 +\frac{3}{4}>0. \end{equation*}Hence the domain of the function \(g\circ f\) is the set \(\{ x: x\not= 0\}\text{.}\)
We observe that the function \(f\circ g\) is defined for \(x=0\) and that the \(g\circ f\) is not. Hence those two functions are not equal.
-
-
We can take
\begin{equation*} h(x)=x^2-1, \ i(x)=|x| \text{, and }j(x)=3x-2. \end{equation*}Then
\begin{equation*} (j\circ i\circ h)(x)=j(i(h(x)))=j(i(x^2-1))=j(|x^2-1|)=3|x^2-1|-2=F(x). \end{equation*}
Problem 5.2.5.
[6 marks]
-
Use the horizontal line test to determine which function below is one–to–one. See Figure 5.24 and Figure 5.25.
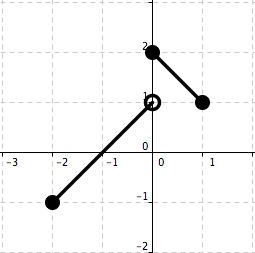
Figure 5.24. Function A 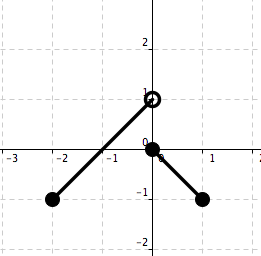
Figure 5.25. Function B Circle the correct answer:
One-to-oneNot one-to-oneA BA B -
Let f be the one–to–one function you picked above.
Draw the graph of f−1.
-
Complete the following table and fill in all boxes:
Domain of f=Range of f=Domain of f−1=Range of f−1=(f∘f−1)(x)= ,for all x∈[◻,◻](f−1∘f)(x)= , for all x∈[◻,◻]((f−1)−1)(x)= , for all x∈[◻,◻]
-
We note that there is a horizontal line that intersects the graph of Function B at two points. This means, by the horizontal line test, that Function B is not a one–to–one function. We \textit{see} that every horizontal line intersects the graph of Function A at most one point. Hence, Function A is a one–to–one.
See Figure 5.26 and Figure 5.27.
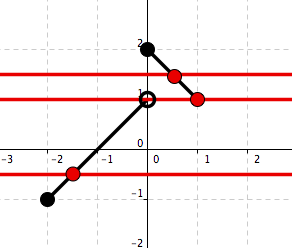
Figure 5.26. Function \(A\) 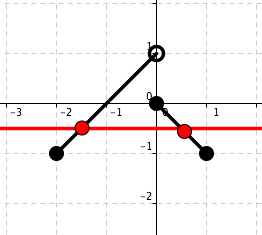
Figure 5.27. Function \(B\) Therfore:
\begin{equation*} \begin{array}{c||c} \text{One-to-one}\amp \text{Not one-to-one} \\ \hline A \amp B\\ \end{array} \end{equation*} -
See Figure 5.28.
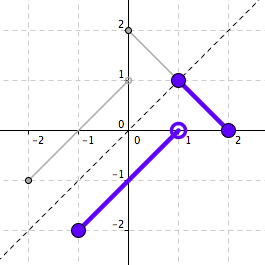
Figure 5.28. Graph of \(f^{-1}\text{.}\) -
Complete the following table and fill in all boxes:
\begin{equation*} \begin{array}{ccl} \text{Domain of }f\amp=\amp [-2,1]\\ \hline \text{Range of }f\amp = \amp [-1,2]\\ \hline \text{Domain of }f^{-1}\amp = \amp [-1,2]\\ \hline \text{Range of }f^{-1} \amp = \amp [-2,1]\\ \hline (f\circ f^{-1})(x) \amp = \amp x , \text{for all }x\in [-1,2] \\ \hline (f^{-1}\circ f)(x)\amp = \amp x, \text{ for all }x\in [-2,1] \\ \hline ((f^{-1})^{-1})(x) \amp = \amp f(x), \text{ for all }x\in [-2,1] \\ \end{array} \end{equation*}
-
Subsection 5.2.2 Midterm 2
Problem 5.2.6.
[6 marks] Solve the following equations:
4x+7−2(x−3)=6x+8−2(2x−4)
4x2+1=4x
52x−5x−12=0.
-
This is a linear equation. We note that the given equation is equivalent to the equation
\begin{equation*} 4x+7-2x+6=6x+8-4x+8\Leftrightarrow 2x+13=2x+16. \end{equation*}From
\begin{equation*} 2x+13=2x+16\Leftrightarrow 2x-2x=16-13\Leftrightarrow 0=3 \end{equation*}we conclude that the given equation has no solution.
-
The given equation is a quadratic equation. From
\begin{equation*} 4x^2+1=4x\Leftrightarrow 4x^2-4x+1=0\Leftrightarrow (2x-1)^2=0\Leftrightarrow 2x-1=0\ \end{equation*}it follows that \(x=\frac{1}{2}\) is the only equation of the given equation.
-
We note that the substitution \(t=5^x\) gives a quadratic equation \(t^2-t-12=0\text{.}\)
The quadratic formula implies
\begin{equation*} t=\frac{1\pm\sqrt{1+49}}{2}=\frac{1\pm\sqrt{49}}{2}=\frac{1\pm7}{2}. \end{equation*}Since \(t=5^x>0\text{,}\) we reject the negative solution of the quadratic equation above, \(t=\frac{1-7}{2}=-3\text{.}\)
Hence
\begin{equation*} t=\frac{1+7}{2}=4\Leftrightarrow 5^x=4\Leftrightarrow x=\log_5 4. \end{equation*}
Problem 5.2.7.
[6 marks] Let the line ℓin the xy–plane be given by the equation 2x+y=1 and let P be the point with the coordinates (−1,1).
Find the point on the line ℓ that is closest to the point P.
Draw the line ℓ, the point P, and the point that you obtained in part (a).
-
From
\begin{equation*} x+y=1\Leftrightarrow y=-2x+1 \end{equation*}we conclude that all points on the line \(/ell\) are of the form \((x,-2x+1)\text{,}\) \(x\in \mathbb{R}\text{.}\)
It follows that the distance between a point \((x,-2x+1)\) on the line and the point \((-1,1)\) is given by
\begin{equation*} d=\sqrt{(x-(-1))^2+(-2x+1-1)^2}=\sqrt{x^2+2x+1+4x^2}=\sqrt{5x^2+2x+1}. \end{equation*}The quadratic function \(f(x)=5x^2+2x+1\) achieves its minimum at the first coordinate of the vertex of its graph:
\begin{equation*} x=-\frac{b}{2a}=-\frac{2}{10}=-\frac{1}{5}. \end{equation*}The point on the line\(\ell\)} that is closest to the point \(P\) is
\begin{equation*} M=\left( -\frac{1}{5},-2\cdot \left( -\frac{1}{5}\right)+1\right)=\left( -\frac{1}{5},\frac{2}{5}+1\right)=\left( -\frac{1}{5},\frac{7}{5}\right). \end{equation*} -
See Figure 5.29.
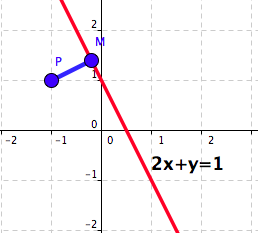
Figure 5.29. The line \(\ell\text{,}\) the point \(P\text{,}\) and the point \(M\text{.}\)
Problem 5.2.8.
[6 marks] Suppose that you are given an open top box with the square base. Let x be the length of the side of the base and let the volume of the box be V=1. See Figure 5.30
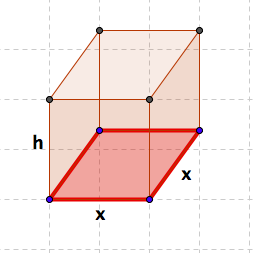
Express the surface area of the box in terms of two power functions of x.
What is the domain of the obtained function?
What will happen if x is very big? Very small?
-
The surface area is the sum of the areas of the square that is the bottom of the box and the areas of the four sides. Note that each side is a rectangle with sides \(x\) and \(h\text{.}\) Hence the surface area is given by \(S=x^2+4hx\text{.}\)
Next we express the variable \(h\) in terms of the variable \(x\text{.}\)
The volume of the box is given as the product of the area of the base and the hight of the box. Since the base is a square with the side \(x\) we have that \(V=x^2h\text{.}\)
It is given that \(V=1\) so
\begin{equation*} 1=x^2h \Rightarrow h=\frac{1}{x^2}. \end{equation*}It follows that
\begin{equation*} S=x^2+4\cdot \frac{1}{x^2}\cdot x=x^2+4\cdot\frac{1}{x}. \end{equation*} -
Observe that the expression for \(S\) obtained above is defined for all \(x\not= 0\text{.}\) Since \(x\) is the length of the side of the base, we have that \(x\) must be a positive real number.
Thus, the domain of the function \(S\) is the set \(\{x\in \mathbb{R}|x>0\}=(0,\infty)\text{.}\)
-
If \(x\) is a large number then the term \(\frac{4}{x}\) is very small and \(S\approx x^2\text{.}\) This means that the box will have a large base but that the hight of the box will be small.
If \(x\) is a small number then the term \(x^2\) is very small and \(S\approx \frac{4}{x}\text{.}\) This means that the box will have a large hight but that the base of the box will be small.
Problem 5.2.9.
[6 marks] Let f(x)=x2+2x2−x−2.
Determine the domain of f.
Determine all zeros of f.
Determine all vertical asymptotes of f.
Determine the y-intercept of f.
Determine the long range behaviour of f.
Determine the intervals where f(x)>0 and where f(x)<0.
-
Since \(f\) is a rational function, its domain is the set of all real numbers for which the denominator of \(f\) is not equal to 0.
We solve the equation \(x^2-x-2=0\) by using the quadratic formula (or any other method):
\begin{equation*} x=\frac{1\pm\sqrt{1+8}}{2}=\frac{1\pm 3}{2}. \end{equation*}Therefore, the domain of the function \(f\) is the set \(\{x\in \mathbb{R}: x\not= -1, x\not= 2\}\)
. Note that
\begin{equation*} f(x)=\frac{x^2+1}{x^2-x-2}=\frac{x^2+1}{(x+1)(x-2)}. \end{equation*} -
We observe that \(x^2\geq 0\) for all real numbers. Thus, \(x^2+2\gt 0\) for all real numbers which implies that the numerator of \(f\) is never equal to 0.
This means that \(f\) has no zeros.
The function \(f\) is not defined at \(x=-1\) and \(x=2\text{.}\) Since the numerator of \(f\) does not cancel at these values of \(x\) , we conclude that the vertical asymptotes are lines \(x=-1\) and \(x=2\text{.}\)
The \(y\)–intercept of \(f\) is given by \(f(0)=\frac{0^2+1}{0^2-0-2}=-\frac{1}{2}\text{.}\)
-
We use the fact that for all \(x\) with large absolute values a polynomial in \(x\) behaves as its leading term. Thus
\begin{equation*} f(x)=\frac{x^2+1}{x^2-x-2}\approx \frac{x^2}{x^2}=1. \end{equation*}This means that the line \(y=1\) is a horizontal asymptote to the graph of \(f\text{.}\)
-
From \(f(x)=\frac{x^2+1}{x^2-x-2}\) and the fact that \(x^2+1>0\) for all real number \(x\) we conclude that
\begin{equation*} f(x)>0\Leftrightarrow x^2-x-2>0. \end{equation*}The graph of the parabola \(y=x^2-x-2=(x+1)(x-2)\text{,}\) a “happy” parabola with zeros at \(x=-1\) and \(x=2\text{,}\) gives that
\begin{equation*} x^2-x-2\gt 0 \Leftrightarrow x\in (-\infty,-1)\cup (2,\infty) \text{ and } x^2-x-2\lt 0 \Leftrightarrow x\in (-1,2). \end{equation*}Therefore
\begin{equation*} f(x)\gt 0 \Leftrightarrow x\in (-\infty,-1)\cup (2,\infty) \text{ and } f(x)\lt 0 \Leftrightarrow x\in (-1,2). \end{equation*}
Problem 5.2.10.
[6 marks] Let f(x)=2log(x+1)+2.
Determine the domain of the function f.
Determine all zeros of the function f.
Find the inverse function f−1 of the function f.
Starting with the graph of the function y=logx and by using the appropriate transformations, sketch a graph of the functionf.
-
The domain of the function \(f\) is given by
\begin{equation*} \{x\in \mathbb{R}: x+1\gt 0\}=\{x\in \mathbb{R}: x\gt -1\}=(-1,\infty). \end{equation*} -
We solve the equation \(f(x)=2\log(x+1)+2=0\text{.}\)
It follows that
\begin{equation*} 2\log(x+1)+2=0\Leftrightarrow 2\log(x+1)=-2\Leftrightarrow \log(x+1)=-1\Leftrightarrow x+1=10^{-1}. \end{equation*}Hence \(x=-1+10^{-1}=-0.9\) is the only zero of the function \(f\text{.}\)
-
To find \(f^{-1}\) we start with \(y=2\log(x+1)+2\text{,}\) interchange the roles of “\(y\)”and “\(x\)” and then solve
\begin{equation*} x=2\log(y+1)+2 \end{equation*}for \(y\text{.}\)
It follows that
\begin{equation*} x=2\log(y+1)+2\Leftrightarrow 2\log(y+1)=x-2\Leftrightarrow \log(y+1)=\frac{x-2}{2} \end{equation*}\begin{equation*} \Leftrightarrow y+1=10^{\frac{x-2}{2}}. \end{equation*}Hence
\begin{equation*} f^{-1}(x)=-1+10^{\frac{x-2}{2}}. \end{equation*} -
See Figure 5.31 – Figure 5.34.
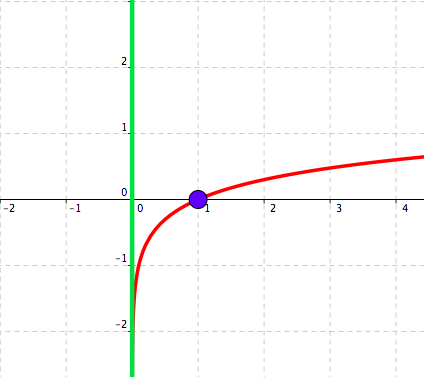
Figure 5.31. Function \(y=\log x\text{.}\) 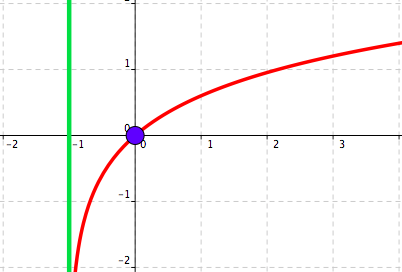
Figure 5.32. Horizontal shift to the left by 1. 
Figure 5.33. Vertical stretch by a factor of 2. 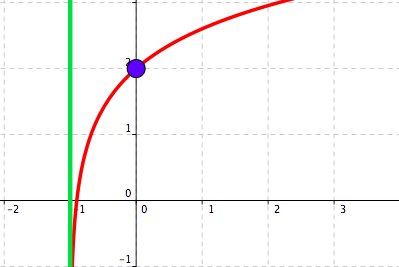
Figure 5.34. Vertical shift up by 2.
