Rational Functions

Section 2.5 Rational Functions

It has been said that man is a rational animal. All my life I have been searching for evidence which could support this. — Bertrand Arthur William Russell, 3rd Earl Russell, British philosopher, logician, mathematician, historian, writer, social critic and political activist, 1872 – 1970

Why rational functions: Rational functions model data with singularities.

Example 2.5.1. From Vancouver, BC, to Abbotsford, BC.

The distance between the City of Vancouver, BC, and the City of Abbotsford, BC, is estimated to be 68.5 km.See Figure 2.45

Figure 2.45. Assume that the distance between the two cities is 68.5 km.

Complete the table below, i.e. find the travelling time $t$ from Vancouver, BC, to Abbotsford, BC, if the average speed $s$ (in km/h) is given.

Model: For $\text{Distance}=d=68.5$ km, from

\begin{equation*} \text{Distance} = \text{(average speed)} \cdot \text{(travelling time)} \end{equation*}

it follows that

\begin{equation*} t=\frac{68.5}{s}\mbox{ hours}. \end{equation*}

\begin{equation*} \begin{array}{l|c|c} \text{Moving object}\amp s= \text{ average speed in km/h}\amp t=\text{ travelling time in hours}\\ \hline \hline \text{Car}\amp100 \amp\\ \hline \text{Racing motorbike}\amp 300\amp \\ \hline \text{Racing bicycle}\amp 38\amp \\ \hline \text{Horse}\amp 44\amp \\ \hline \text{Human (walk)}\amp 5.4\amp \\ \hline \text{Snail}\amp 10^{-3}\amp \\ \hline \text{Light}\amp 1.079\cdot 10^{9}\amp \\ \end{array} \end{equation*}

Solution

\begin{equation*} \begin{array}{l|c|c} \text{vehicle}\amp s= \text{ average speed in km/h}\amp t=\text{ travelling time in hours}\\ \hline \hline \text{Car}\amp100 \amp 0.685\\ \hline \text{Racing motorbike}\amp 300\amp 0.2283333333\\ \hline \text{Racing bicycle}\amp 38\amp 1.8\\ \hline \text{Horse}\amp 44\amp 1.55\\ \hline \text{Walk}\amp 5.4\amp 12.68\\ \hline \text{Snail}\amp 10^{-3}\amp 68500\\ \hline \text{Light}\amp 1.079\cdot 10^{9}\amp 6.244302644\cdot 10^{-8}\\ \end{array} \end{equation*}

Old friend: Function $\displaystyle f(x)=\frac{1}{x}\text{.}$ See Figure 2.46.

Figure 2.46. Function $\displaystyle f(x)=\frac{1}{x}$

Quick facts:

\begin{equation*} \begin{array}{ll||ll} \text{Domain:}\amp \mathbb{R}\backslash \{ 0\}\amp \text{ VA:}\amp x=0\\ \hline \text{Range:}\amp \mathbb{R}\backslash \{ 0\}\amp \text{ HA:}\amp y=0\\ \end{array} \end{equation*}

\begin{equation*} \text{This is a decreasing function} \end{equation*}

How to introduce your friend $\displaystyle f(x)=\frac{1}{x}$ in a few words: His nickname is Inverse Proportion. He is very odd: if you give him less than one he will return you more than one, if you give him more than one, he will return less than one. If you take more than one he will ask for less than one, if you take less than one he will ask for more than one. Just make sure that you give something or that you take something. Otherwise …

Rational functions. Any function of the form

\begin{equation*} R(x)=\frac{p(x)}{q(x)} \end{equation*}

where $p(x)$ and $q(x)\text{,}$ $q(x)\not= 0\text{,}$ are polynomials is called a rational function.

Example 2.5.2. Not rational?

Which of the following functions is NOT rational?

$\displaystyle f(x)= 3x^2+5x-2$
$\displaystyle \displaystyle g(x)=\frac{1}{x}$
$\displaystyle \displaystyle h(x)=\frac{3x^3-5x^2+7x-1}{4x^5+3x-1}$
$\displaystyle i(x)= \frac{x}{x}$
$\displaystyle j(x)= x^{-0.5}=\frac{1}{\sqrt{x}}$

Solution

Since $\displaystyle f(x)= 3x^2+5x-2=\frac{3x^2+5x-2}{1}$ and since $p(x)=3x^2+5x-2$ and $q(x)=1$ are polynomials, this function is a rational function.
Since $\displaystyle g(x)=\frac{1}{x}$ and since $p(x)=1$ and $q(x)=x$ are polynomials, this function is a rational function.
Since $\displaystyle h(x)=\frac{3x^3-5x^2+7x-1}{4x^5+3x-1}$ and since $p(x)=3x^3-5x^2+7x-1$ and $q(x)=4x^5+3x-1$ are polynomials, this function is a rational function.
Since $i(x)= \frac{x}{x}$ and since $p(x)=x$ and $q(x)=x$ are polynomials, this function is a rational function.
Since $x\mapsto 1$ is a polynomial and since the function in the denominator $x\mapsto \sqrt{x}$ is not a polynomial, the function $j(x)= x^{-0.5}=\frac{1}{\sqrt{x}}$ is NOT a rational function.

Quick facts: Let a rational function

\begin{equation*} R(x)=\frac{a_nx^n+a_{n-1}x^{n-1}+\ldots+a_1x+a_0}{b_mx^m+b_{m-1}x^{m-1}+\ldots+b_1x+b_0} \end{equation*}

be given.

Domain. The function $R$ is defined for all real numbers $x$ for which its denominator is not equal to $0\text{.}$

In other words

\begin{equation*} \text{Domain of }R=\{x\in \mathbb{R}:b_mx^m+b_{m-1}x^{m-1}+\ldots+b_1x+b_0\not=0\}. \end{equation*}

Note that the number of real numbers at which $R$ is NOT defined is at most $m\text{.}$
Range. Needs further investigation. Weird things may happen. See Figure 2.47 and Figure 2.48.

Figure 2.47. Three rational functions – What do you observe?

Figure 2.48. Three more rational functions – What do you observe?
Zeros: If $\displaystyle R(x)=\frac{p(x)}{q(x)}$ is a rational function and $x_0\in\mathbb{R}\text{,}$ then

\begin{equation*} R(x_0)=0\Leftrightarrow (p(x_0)=0\text{ and }q(x_0)\not=0). \end{equation*}
Example 2.5.3. Zeros?

Let

\begin{equation*} S(x)=\frac{x-1}{x^2+1}\text{ and }T(x)=\frac{x-1}{x^2-1}. \end{equation*}

Solve
1. $\displaystyle S(x) =0$
2. $\displaystyle T(x) =0$
Solution
The question is to find all zeros of the function $S\text{.}$

Let $p(x)=x-1$ and $q(x)=x^2+1\text{.}$ Then $\displaystyle S(x) =\frac{x-1}{x^2+1}=\frac{p(x)}{q(x)}\text{.}$

Observe that the only zero of the polynomial $p(x)=x-1\text{,}$ the polynomial in the numerator of the function $S\text{,}$ is the number $x_0=1\text{.}$ From $q(x_0)=q(1)=2\not=0\text{,}$ it follows that $x_0=1$ is the only zero of the rational function $S\text{:}$

\begin{equation*} S(1)=\frac{1-1}{1^2+1}=\frac{0}{2}=0. \end{equation*}

The question is to find all zeros of the function $T\text{.}$

Let $p(x)=x-1$ and $r(x)=x^2-1\text{.}$ Then $\displaystyle T(x) =\frac{x-1}{x^2-1}=\frac{p(x)}{r(x)}\text{.}$

Observe that the only zero of the polynomial $p(x)=x-1\text{,}$ the polynomial in the numerator of the function $T\text{,}$ is the number $x_0=1\text{.}$ From $r(x_0)=r(1)=1^2-1=0\text{,}$ it follows that $x_0=1$ is not a zero of the rational function $T\text{.}$

Therefore the equation $T(x)=0$ has no solution.

Note: Observe that, for all real numbers $x\not=\pm 1\text{,}$

\begin{equation*} T(x)=\frac{x-1}{x^2-1}=\frac{x-1}{(x-1)(x+1)}=\frac{1}{x+1}. \end{equation*}

What are the zeros fo the function $T\text{?}$
Vertical asymptotes: If the rational function $R(x)$ is NOT defined at the real number $a$ then the vertical line $x=a$ is a possible vertical asymptote.

BIG question: If

\begin{equation*} R(x)=\frac{p(x)}{q(x)}=\frac{a_nx^n+a_{n-1}x^{n-1}+\ldots+a_1x+a_0}{b_mx^m+b_{m-1}x^{m-1}+\ldots+b_1x+b_0} \end{equation*}

what can we tell about $R(x)$ if $x$ is such that $|x|$ is HUGE?

See Figure 2.49 .

Figure 2.49. What can we tell about a rational function if $x$ is such that $|x|$ isHUGE?

Main tools:

What can we tell about the size of $\displaystyle \frac{1}{x^k}$ if $k$ is a natural number and $x$ is such that $|x|$ is HUGE?
How to divide two polynomials?
Example 2.5.4. Division of polynomials.
1. Divide the polynomial $p(x)=x^4+2x$ by the polynomial $q(x)=x^2-1\text{.}$
2. Divide the polynomial $p(x)=x^3-3x$ by the polynomial $q(x)=x^2-4\text{.}$
3. Divide the polynomial $s(x)=x^2+1$ by the polynomial $q(x)=x^2-1\text{.}$
Solution
First we demonstrate how to use long division to divide two polynomials,

Recall that what is being divided is called the dividend, which is divided by the divisor, and the result is called the quotient.

In this example the dividend is the polynomial $p(x)=x^4+2x$ and the divisor is the polynomial $q(x)=x^2-1\text{.}$ Observe that the degree of the polynomial $p$ equals to 4 and the he degree of the polynomial $q$ equals to 2. This means that the degree of the quotient will be equal to $4-2=2\text{.}$

Step 1: Write

\begin{equation*} \begin{array}{cccccccccc} x^4\amp \amp \amp +2x\amp \amp \div \amp x^2 -1\amp \amp \\ \end{array} \end{equation*}

Step 2: Divide the leading term of the dividend $x^4$ by the leading term of the divisor $x^2$ to obtain $\frac{x^4}{x^2}=x^2$ and write

\begin{equation*} \begin{array}{cccccccccc} x^4\amp \amp \amp +2x\amp \amp \div \amp x^2 -1\amp = x^2\amp \\ \end{array} \end{equation*}

Step 3: Multiply the divisor $x^2-1$ by $x^2$ (the monomial obtained in Step 2) to get $x^4-x^2$ and write

\begin{equation*} \begin{array}{cccccccccc} x^4\amp \amp \amp +2x\amp \amp \div \amp x^2 -1\amp \ x^2\amp \\ x^4\amp \amp -x^2\amp \amp \amp \amp \amp \amp \\ \hline \end{array} \end{equation*}

Step 4: Find the difference between the dividend and the polynomial obtained in Step 3, $(x^4+2x)-(x^4-x^2)=x^2+2x$ and write

\begin{equation*} \begin{array}{cccccccccc} x^4\amp \amp \amp +2x\amp \amp \div \amp x^2 -1\amp =x^2\amp \\ x^4\amp \amp -x^2\amp \amp \amp \amp \amp \amp \\ \hline \amp \amp x^2\amp +2x\amp \amp \amp \amp \amp \\ \end{array} \end{equation*}

Step 5: Treat the polynomial obtained in Step 4 as the new dividend and repeat Steps 1-4 until the (possibly multiple times repeated) Step 4 produces a polynomial of a degree that is less than the degree of the divisor:

\begin{equation*} \begin{array}{cccccccccc} x^4\amp \amp \amp +2x\amp \amp \div \amp x^2 -1\amp =x^2+1\amp \\ x^4\amp \amp -x^2\amp \amp \amp \amp \amp \amp \\ \hline \amp \amp x^2\amp +2x\amp \amp \amp \amp \amp \\ \amp \amp x^2\amp \amp -1\amp \amp \amp \amp \\ \hline \amp \amp \amp 2x\amp +1\amp \amp \amp \amp \\ \end{array} \end{equation*}

Step 6: Conclude

\begin{equation*} \frac{x^4+2x}{x^2-1}=x^2+1+\frac{2x+1}{x^2-1} \end{equation*}

Sometimes is easier and faster to use the properties of the basic algebraic operations to divide two polynomials.

For example:

\begin{equation*} \frac{x^3-3x}{x^2-4}=\frac{x^3-4x+4x-3x}{x^2-4}=\frac{x(x^2-4)+x}{x^2-4}= \end{equation*}

\begin{equation*} \frac{x(x^2-4)}{x^2-4}+\frac{x}{x^2-4}=1+\frac{x}{x^2-4} \end{equation*}

Observe

\begin{equation*} \frac{x^2+1}{x^2-1}=\frac{x^2-1+2}{x^2-1}=1+\frac{2}{x^2-1} \end{equation*}

Example 2.5.5. A Taste Of Calculus.

Sketch the graphs of the following rational functions:

$\displaystyle \displaystyle f(x)=\frac{x^4+2x}{x^2-1}$
$\displaystyle \displaystyle g(x)=\frac{x^3-3x}{x^2-4}$
$\displaystyle \displaystyle g(x)=\frac{x^2+1}{x^2-1}$

Solution

- Domain: Let $p(x)= x^4+2x$ and $q(x)=x^2-1\text{.}$ Then $\displaystyle f(x)=\frac{x^4+2x}{x^2-1}=\frac{p(x)}{q(x)}\text{.}$
  
  We note that that
  
  \begin{equation*} q(x)=x^2-1=0\Leftrightarrow (x=1 \text{ or } x=-1) \end{equation*}
  
  which implies that the domain of the function $f$ is the set $\{x\in\mathbb{R}:x\not=\pm1\}\text{.}$
- Zeros:
  
  From
  
  \begin{equation*} p(x)=x^4+2x=x(x^3+2)=0\Leftrightarrow (x=0 \text{ or }x=\sqrt[3]{2}), \end{equation*}
  
  and
  
  \begin{equation*} q(0)=0^2-1=-1\not=0, \ q(\sqrt[3]{2})=\sqrt[3]{4}-1\not=0 \end{equation*}
  
  we conclude that
  
  \begin{equation*} f(x)=\frac{x^4+2x}{x^2-1}=0\Leftrightarrow (x=0 \text{ or }x=\sqrt[3]{2}). \end{equation*}
- Vertical asymptotes:
  
  From
  
  \begin{equation*} q(x)=x^2-1=0\Leftrightarrow (x=1 \text{ or } x=-1) \end{equation*}
  
  and
  
  \begin{equation*} p(1)=1^4+2\cdot 1=3\not=0 \text{ and } p(-1)=-1\not=0 \end{equation*}
  
  it follows that $x=1$ and $x=-1$ are vertical asymptotes to the graph of the function $f\text{.}$
- The $y$–intercept:
  
  We evaluate $f(0)=0$ and conclude that the point $(0,0)$ is the $y$–intercept.
- The long range behaviour:
  
  Recall from Example 2.5.5 that
  
  \begin{equation*} f(x)=\frac{x^4+2x}{x^2-1}=x^2+1+\frac{2x+1}{x^2-1}. \end{equation*}
  
  It follows that for real numbers $x$ such that the value of $|x|$ is large we have
  
  \begin{equation*} f(x)\approx x^2+1\approx x^2. \end{equation*}
- Sign of $f(x):$
  
  From
  
  \begin{equation*} f(x)=\frac{x^4+2x}{x^2-1}=\frac{x(x^3+2)}{(x+1)(x-1)} \end{equation*}
  
  we observe that the sign of $f(x)$ depends on the signs of four factors:
  
  \begin{equation*} x,x^3+2,x+1, \text{ and }x-1. \end{equation*}
  
  If $x\in \text{dom }(f)$ is such that an even number of those factors is negative then $f(x)\gt 0\text{.}$ Otherwise, i.e. if an odd number of factors is negative then $f(x)\lt 0\text{.}$
  
  We summarize all possible cases in the following table.
  
  \begin{equation*} \begin{array}{c||c|c|c|c|c|c|c|c|c} \amp \amp-\sqrt[3]{2}\amp \amp -1\amp \amp 0\amp \amp 1\amp\\ \hline x^3+2\amp -\amp 0\amp +\amp \amp+\amp \amp+\amp \amp+\\ \hline x+1\amp -\amp\amp-\amp 0\amp+\amp \amp +\amp \amp +\\ \hline x\amp -\amp \amp -\amp \amp-\amp 0\amp +\amp \amp+\\ \hline x-1\amp-\amp \amp -\amp \amp -\amp \amp -\amp 0\amp +\\ \hline \hline f(x)\amp +\amp 0\amp -\amp \text{ND}\amp +\amp 0\amp -\amp \text{ND}\amp +\\ \end{array} \end{equation*}
- For the graph, see Figure 2.50.
  
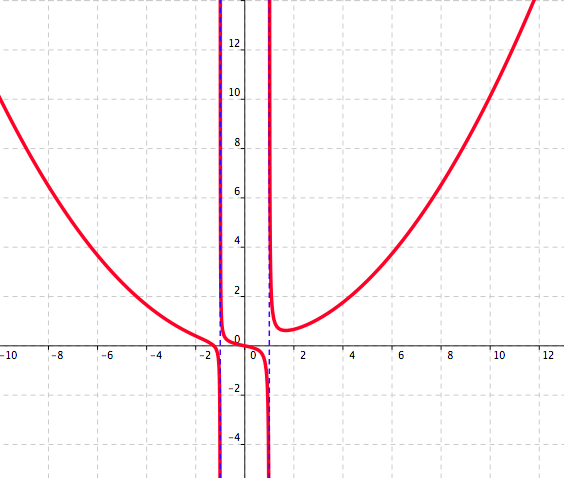
  Figure 2.50. A graph of the function $\displaystyle f(x)=\frac{x^4+2x}{x^2-1}\text{.}$
- Domain: Let $p(x)= x^3-3x$ and $q(x)=x^2-4\text{.}$ Then $\displaystyle g(x)=\frac{x^3-3x}{x^2-4}=\frac{p(x)}{q(x)}\text{.}$
  
  We note that that
  
  \begin{equation*} q(x)=x^2-4=0\Leftrightarrow (x=2 \text{ or } x=-2) \end{equation*}
  
  which implies that the domain of the function $g$ is the set $\{x\in\mathbb{R}:x\not=\pm2\}\text{.}$
- Zeros:
  
  From
  
  \begin{equation*} p(x)=x^3-3x=x(x^2-3)=0\Leftrightarrow (x=0 \text{ or }x=\pm\sqrt{3}), \end{equation*}
  
  and
  
  \begin{equation*} q(0)=0^2-4=-4\not=0, \ q(\pm\sqrt{3})=3-4\not=0 \end{equation*}
  
  we conclude that
  
  \begin{equation*} g(x)=\frac{x^3-3x}{x^2-4}=0\Leftrightarrow (x=0 \text{ or }x=\pm\sqrt{3}). \end{equation*}
- Vertical asymptotes:
  
  From
  
  \begin{equation*} q(x)=x^2-4=0\Leftrightarrow (x=2 \text{ or } x=-2) \end{equation*}
  
  and
  
  \begin{equation*} p(2)=2^3+3\cdot 2=14\not=0 \text{ and } p(-2)=-2\not=0 \end{equation*}
  
  it follows that $x=2$ and $x=-2$ are vertical asymptotes to the graph of the function $g\text{.}$
- The $y$–intercept:
  
  We evaluate $g(0)=0$ and conclude that the point $(0,0)$ is the $y$–intercept.
- The long range behaviour:
  
  Recall from Example 2.5.5 that
  
  \begin{equation*} g(x)=\frac{x^3-3x}{x^2-4}=x+\frac{x}{x^2-4}. \end{equation*}
  
  It follows that for real numbers $x$ such that the value of $|x|$ is large we have
  
  \begin{equation*} g(x)\approx x. \end{equation*}
  
  In other words, it follows that the line $y=x$ is a slant asymptote to the graph of the function $g\text{.}$
- Sign of $g(x):$
  
  From
  
  \begin{equation*} g(x)=\frac{x^3-3x}{x^2-4}=\frac{x(x^2-3)}{(x+2)(x-2)}=\frac{x(x+\sqrt{3})(x-\sqrt{3})}{(x+2)(x-2)} \end{equation*}
  
  we observe that the sign of $g(x)$ depends on the signs of five factors:
  
  \begin{equation*} x,x+\sqrt{3}, x-\sqrt{3},x+2, \text{ and }x-2. \end{equation*}
  
  If $x\in \text{dom }(g)$ is such that an even number of those factors is negative then $g(x)\gt 0\text{.}$ Otherwise, i.e. if an odd number of factors is negative then $g(x)\lt 0\text{.}$
  
  We summarize all possible cases in the following table.
  
  \begin{equation*} \begin{array}{c||c|c|c|c|c|c|c|c|c|c|c} \amp \amp-2\amp \amp -\sqrt{3}\amp \amp 0\amp \amp \sqrt{3}\amp \amp 2\amp\\ \hline x+2\amp -\amp 0\amp +\amp \amp +\amp \amp +\amp \amp +\amp \amp +\\ \hline x+\sqrt{3}\amp -\amp \amp -\amp 0\amp +\amp \amp+\amp \amp+\amp \amp+\\ \hline x\amp -\amp \amp -\amp \amp -\amp 0\amp +\amp \amp +\amp \amp+\\ \hline x-\sqrt{3}\amp -\amp \amp -\amp \amp -\amp \amp -\amp 0\amp +\amp \amp +\\ \hline x-2\amp -\amp \amp -\amp \amp -\amp \amp -\amp \amp -\amp 0\amp +\\ \hline \hline f(x)\amp-\amp \text{ND}\amp +\amp 0\amp -\amp 0\amp +\amp 0\amp -\amp \text{ND}\amp +\\ \end{array} \end{equation*}
- For the graph, see Figure 2.51.
  
  Figure 2.51. A graph of the function $\displaystyle g(x)= g(x)=\frac{x^3-3x}{x^2-4}\text{.}$
- Domain: Let $p(x)= x^2+1$ and $q(x)=x^2-1\text{.}$ Then $\displaystyle h(x)=\frac{x^2+1}{x^2-1}=\frac{p(x)}{q(x)}\text{.}$
  
  We note that that
  
  \begin{equation*} q(x)=x^2-1=0\Leftrightarrow (x=1 \text{ or } x=-1) \end{equation*}
  
  which implies that the domain of the function $h$ is the set $\{x\in\mathbb{R}:x\not=\pm1\}\text{.}$
- Zeros:
  
  From
  
  \begin{equation*} p(x)=x^2+1\geq 1\gt 0 \end{equation*}
  
  on its domain, i.e. that the graph of $h$ does not have any $x$-intercepts. we conclude that $h(x)\not=0$ on its domain, i.e., that the graph of $h$ does not have any $x$–intercepts.
- Vertical asymptotes:
  
  From
  
  \begin{equation*} q(x)=x^2-1=0\Leftrightarrow (x=1 \text{ or } x=-1) \end{equation*}
  
  and
  
  \begin{equation*} p(-1)= p(1)=2\not=0 \end{equation*}
  
  it follows that $x=1$ and $x=-1$ are vertical asymptotes to the graph of the function $g\text{.}$
- The $y$–intercept:
  
  We evaluate $h(0)=-1$ and conclude that the point $(0,-1)$ is the $y$–intercept.
- The long range behaviour:
  
  Recall from Example 2.5.5 that
  
  \begin{equation*} h(x)=\frac{x^2+1}{x^2-1}=1+\frac{2}{x^2-1}. \end{equation*}
  
  It follows that for real numbers $x$ such that the value of $|x|$ is large we have
  
  \begin{equation*} h(x)\approx 1. \end{equation*}
  
  In other words, it follows that the line $y=1$ is a horizontal asymptote to the graph of the function $h\text{.}$
- Sign of $h(x):$
  
  From
  
  \begin{equation*} h(x)=\frac{x^2+1}{x^2-1}=\frac{x^2+1}{(x+1)(x-1)} \end{equation*}
  
  we observe that the sign of $g(x)$ depends on the signs of two factors:
  
  \begin{equation*} x+1 \text{ and }x-1. \end{equation*}
  
  If $x\in \text{dom }(h)$ is such that an even number of those factors is negative then $h(x)\gt 0\text{.}$ Otherwise, i.e. if an odd number of factors is negative then $h(x)\lt 0\text{.}$
  
  We summarize all possible cases in the following table.
  
  \begin{equation*} \begin{array}{c||c|c|c|c|c} \amp \amp -1\amp \amp1\amp\\ \hline x+1\amp -\amp 0\amp +\amp \amp +\\ \hline x-1\amp -\amp \amp- \amp 0\amp +\\ \hline \hline f(x)\amp +\amp \text{ND}\amp - \amp \text{ND}\amp +\\ \end{array} \end{equation*}
- For the graph, see Figure 2.52.
  
  Figure 2.52. A graph of the function $\displaystyle h(x)= h(x)=\frac{x^2+1}{x^2-1}\text{.}$

Section 2.5 Rational Functions

Example 2.5.1. From Vancouver, BC, to Abbotsford, BC.

Example 2.5.2. Not rational?

Example 2.5.3. Zeros?

Example 2.5.4. Division of polynomials.

Example 2.5.5. A Taste Of Calculus.