The Law of Sines and the Law of Cosines

In the triangle $\triangle ABC$ with the usual notation, suppose that $\sin \alpha = \frac{2\sqrt{2}}{3}\text{,}$ that $a = 11$ and that $b = 9\text{.}$ Find $\sin \beta\text{.}$

Solution

By the Law of Sines

\begin{equation*} \frac{a}{\sin \alpha} = \frac{b}{\sin \beta} \Rightarrow \frac{11}{\frac{2\sqrt{2}}{3}} = \frac{9}{\sin \beta}\Rightarrow \sin\beta =\frac{9\cdot\frac{2\sqrt{2}}{3}}{11} = \frac{6\sqrt{2}}{11}. \end{equation*}

🔗

Area of a Triangle: The Law of Sines implies that

$\begin{equation*} \text{Area}(\triangle ABC) = \frac{1}{2} ac \sin \beta. \end{equation*}$

🔗

Solution

See Figure 4.64.

Figure 4.64. Area of $\triangle ABC\text{.}$

In $\triangle ABC$ with the usual notation, let $h$ be the hight to the side $c\text{.}$

Observe that $h=a\sin \beta\text{.}$ Thus, the area of the triangle is given by

\begin{equation*} A=\frac{ch}{2}=\frac{1}{2}\cdot ac\sin\beta . \end{equation*}

Note: Notice that in this formula, $\beta$ represents the anglebetween $a$ and $c\text{.}$

🔗

Example 4.6.2. Use the given area to find a side.

In $\triangle ABC$ with the usual notation, suppose that $\sin \alpha = 2/3\text{,}$ that $b = 9$ and that the area of $\triangle ABC$ is $24$ Find $c\text{.}$

Solution

Note that, in the usual notation, $\alpha$ represents the angle between $b$ and $c\text{,}$ so the area of $\triangle ABC$ is given by

\begin{equation*} A=\frac{1}{2}\cdot bc\sin\alpha\Leftrightarrow c=\frac{2A}{b\sin \alpha}. \end{equation*}

We conclude that in the given triangle

\begin{equation*} c=\frac{2\cdot 24}{9\cdot \frac{2}{3}}=\frac{2\cdot 24}{6}=8. \end{equation*}

🔗

The Law of Cosines. See Figure 4.65.

🔗

See Figure 4.65.

🔗

Figure 4.65. Area of

$\triangle ABC\text{.}$

🔗

We use Figure 4.65.

🔗

Observe that, by the Pythagorean theorem,

$\begin{equation*} b^2 =(c-a\cos\beta)^2+(a\sin\beta)^2= c^2-2ac\cos\beta+a^2\cos^2\beta+a^2\sin^2\beta \end{equation*}$

$\begin{equation*} =c^2-2ac\cos\beta+a^2(\cos^2\beta+\sin^2\beta)=c^2-2ac\cos\beta+a^2. \end{equation*}$

🔗

The fact that

$\begin{equation*} b^2 =a^2+c^2-2ac\cos\beta \end{equation*}$

🔗

is known as the Law of Cosines.

🔗

Note: Observe that the the angle

$\beta$ is between the sides

$a$ and

$c$ and that side

$b$ is opposite to the angle

$\beta\text{.}$ Hence

$\begin{equation*} c^2 =a^2+b^2-2ab\cos\gamma \text{ and } a^2 =b^2+c^2-2bc\cos\alpha \end{equation*}$

🔗

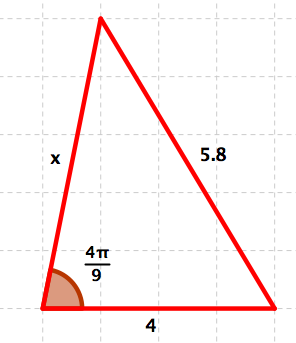
Example 4.6.3. Solve using the Law of Cosines.

Evaluate $x\text{.}$ See Figure 4.66.

Solution

By the Law of Cosines,

\begin{equation*} 5.8^2 =x^2+4^2-2\cdot 4\cdot x\cdot \cos \frac{4\pi}{9}\Leftrightarrow x^2-8x\cos\frac{4\pi}{9}+4^2-5.8^2=x^2-8x\cos\frac{4\pi}{9}-17.64=0. \end{equation*}

We solve the quadratic equation to obtain

\begin{equation*} x=\frac{8\cos\frac{4\pi}{9}\pm\sqrt{64\cos\frac{4\pi}{9}+70.26}}{2}\approx\frac{1.39 \pm9.02}{2} \end{equation*}

and, since $x\gt 0$ (why?), we reject the negative option.

Thus

\begin{equation*} x\approx\frac{1.39+9.02}{2}=5.215. \end{equation*}