Section 5.3 Final Exam
This section contains an old final exam.
Problem 5.3.1.
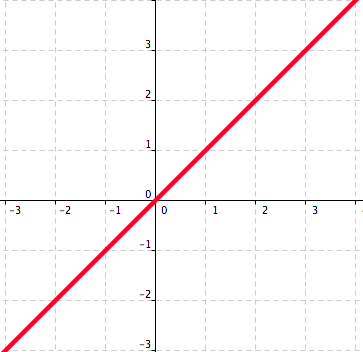
[8 marks] Let \(f\) be the function which associates to an integer \(n\) the number \(\sin n\pi\) if \(n\) is even, and \(\cos n\pi\) if \(n\) is odd.
-
Complete the following table:
\begin{equation*} \begin{array}{c||c|c|c|c|c|c|c} n\amp-2\amp-1\amp0\amp1\amp4\amp100\amp111\\ \hline f(n)\amp\amp\amp\amp\amp\amp\amp\\ \end{array} \end{equation*} -
Express the function \(f\) as a piecewise defined function:
\begin{equation*} f(n)=\left\{ \begin{array}{ll} \hspace{1cm}\amp\text{if}\\ \hspace{1cm}\amp\text{if}\\ \end{array} \right. \end{equation*} State the domain and the range of the function \(f\text{.}\)
Draw a graph of \(f\text{.}\)
-
By definition of \(f\text{:}\)
\begin{equation*} \begin{array}{c||c|c|c|c|c|c|c} n\amp-2\amp-1\amp0\amp1\amp4\amp100\amp111\\ \hline f(n)\amp \sin(-2\pi)=0\amp \cos (-\pi)=-1 \amp \sin(0)=0\amp \cos (\pi)=-1\amp 0 \amp0 \amp-1\\ \end{array} \end{equation*} -
Observe:
\begin{equation*} f(n)=\left\{ \begin{array}{ll} 0\amp\text{if } n \text{ is even}\\ -1\amp\text{if }n \text{ is odd}\\ \end{array} \right. \end{equation*} -
By definition, the domain of the function \(f\) is \(\mathbb{Z}\text{,}\) the set of all integers.
We observe that the range the function \(f\) is the set \(\{-1,0\}\text{.}\)
-
See Figure 5.35.
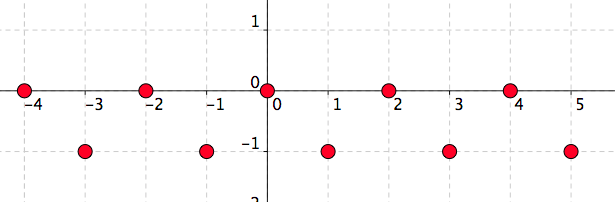
Figure 5.35. The graph of \(f\text{.}\)
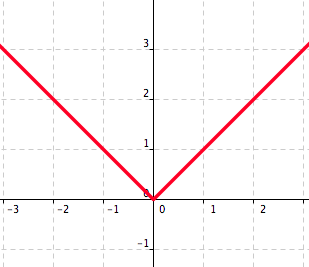
Problem 5.3.2.
[6 marks] The function \(y=f(x)\) is given by its graph. See Figure 5.36.
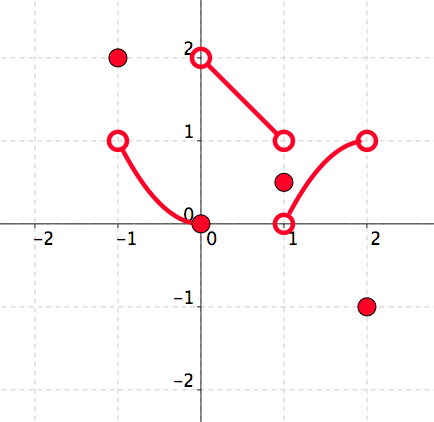
-
Complete the following table:
\begin{equation*} \begin{array}{c||c|c|c|c|c} x\amp-2\amp-1\amp0\amp1\amp2\\ \hline f(x)\amp\amp\amp\amp\amp\\ \end{array} \end{equation*}.
Draw the graph of the function \(g(x)=f(-x)\text{.}\)
Draw the graph of the function \(h(x)=-f(x)\text{.}\)
-
We read from the graph:
\begin{equation*} \begin{array}{c||c|c|c|c|c} x\amp-2\amp-1\amp0\amp1\amp2\\ \hline f(x)\amp\text{Not defined}\amp 2\amp 0\amp 0.5\amp -1\\ \end{array} \end{equation*}.
-
See Figure 5.37.
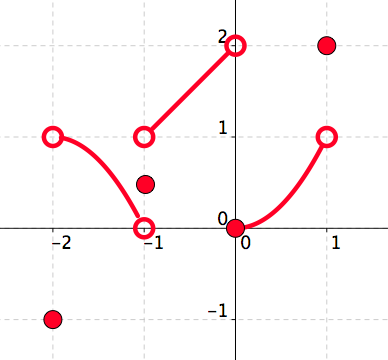
Figure 5.37. The graph of \(g(x)=f(-x)\text{.}\) -
See Figure 5.38.
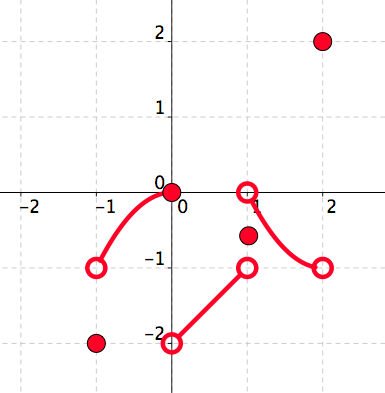
Figure 5.38. The graph of \(h(x)=-f(x)\text{.}\)
Problem 5.3.3.
[6 marks] A soccer team plays in an arena that has a seating capacity of 10,000 spectators. With the ticket price set at \(\$75\text{,}\) the average attendance at recent games has been 5,500. A market survey indicates that for each dollar the ticket price is lowered, the average attendance increases by 50.
Find a function that models the revenue in terms of the ticket price.
Which price will give the maximum revenue? Justify your answer.
-
Let \(x\) represent the ticket price in dollars and let \(A(x)\) represent the average attendance at the price \(x\text{.}\) Observe that, since for each dollar the ticket price is lowered the average attendance increases by 50, the attendance with the ticket price of \(x\) dollars is given by
\begin{equation*} A(x)=5500+50(75-x)=5500+3750-50x=9250-50x. \end{equation*}The revenue is given as the product of the ticket price and the number of the people in the attendance.
It follows that the function
\begin{equation*} R(x)=x\cdot A(x)=x(9250-50x)=-50x^2+9250x \end{equation*}models the revenue \(R(x)\) in terms of ticket price \(x\text{.}\)
-
Note that \(R(x)\) is a quadratic function and that its graph is part of a parabola that opens downward. Thus the maximum revenue is achieved at the vertex of the parabola. The first coordinate of the vertex is given by
\begin{equation*} x=-\frac{9250}{2\cdot (-50)}=92.50 \end{equation*}Therefore the ticket price of \(x=\$92.50\) will yield the maximum revenue.
Note: From \(R(x)=-50x^2+9250x=50x(185-x)\) we obtain that the maximum revenue is \(R(92.50)=50\cdot 92.50\cdot(185-92.50)=4625\cdot 92.50=427812.50\) dollars.
Also, at the price of \(\$92.50\) there will be \(A(92.50)=9250-50\cdot 92.50=4625\) spectators in the arena.
Problem 5.3.4.
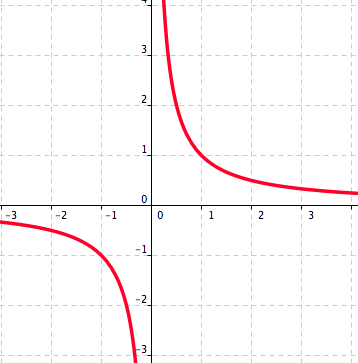
[6 marks] Let \(f(x)=e^{\sqrt{1-x}}+3.\)
Find the domain of the function \(f\text{.}\)
-
Decompose the function \(f\text{,}\) i.e., find functions \(p\text{,}\) \(q\text{,}\) \(r\text{,}\) and \(s\) such that \(f = p\circ q \circ r\circ s\text{.}\)
Note: None of the functions chosen can be the identity function.
Find a formula for the inverse of the function \(f\text{.}\)
-
The domain of the function \(f\) is given by
\begin{equation*} \{x\in \mathbb{R}: 1-x\geq 0\}=\{x\in \mathbb{R}: x\leq 1\}=(\infty, -1]. \end{equation*} -
If we take \(s(x)=1-x\text{,}\) \(r(x)=\sqrt{x}\text{,}\) \(q(x)=e^x\text{,}\) and \(p(x)=x+3\) then
\begin{equation*} (p\circ q \circ r\circ s)(x)=p(q(r(s(x))))=p(q(r(1-x)))=p(q(\sqrt{1-x}))=p(e^{\sqrt{x}})=e^{\sqrt{1-x}}+3=f(x). \end{equation*} -
To find the inverse function of the function \(f\) we apply the following procedure.
Let \(y=e^{\sqrt{1-x}}+3\text{.}\) We interchange the roles of “\(x\)” and “\(y\)” to obtain
\begin{equation*} x=e^{\sqrt{1-y}}+3 \end{equation*}and then we solve this expression for “\(y\)”.
Thus
\begin{equation*} x=e^{\sqrt{1-y}}+3\Leftrightarrow x-3=e^{\sqrt{1-y}}\Leftrightarrow \ln(x-3)=\sqrt{1-y} \end{equation*}\begin{equation*} \Leftrightarrow ((\ln (x-3))^2=1-y\Leftrightarrow y=1-((\ln (x-3))^2. \end{equation*}The inverse function of the function \(f\) is given by \(f^{-1}(x)=1-((\ln (x-3))^2\text{.}\)
Problem 5.3.5.
[12 marks] Find all solutions to the equations:
\(5^{2x}-5^x-12=0\text{.}\)
\(\left[\log (10x)\right]\cdot \left[\log(100x)\right]=(\log x)^2\text{.}\)
\(\sin 2x-\sqrt{2}\cdot \sin x=0\) for values of \(x\) in the interval \([0,2\pi )\text{.}\)
-
Let \(t=5^x\text{.}\) With this substitution the given equation becomes \(t^2-t-12=0\text{.}\)
We solve this quadratic equation:
\begin{equation*} t^2-t-12=0\Leftrightarrow (t-4)(t+3)=0\Leftrightarrow (t=4 \text{ or }t=-3). \end{equation*}Since \(t=5^x>0\text{,}\) we reject the negative value \(t=-3\text{.}\)
It follows
\begin{equation*} 5^x=4\Leftrightarrow x=\log_54. \end{equation*} -
We use the fact that \(\log(10x)=\log 10+\log x=1+\log x\) and \(\log(100x)=\log 100+\log x=2+\log x\) to obtain
\begin{equation*} \left[\log (10x)\right]\cdot \left[\log(100x)\right]=(\log x)^2\Leftrightarrow (1+\log x)\cdot(2+\log x)=(\log x)^2\Leftrightarrow \end{equation*}\begin{equation*} 2+3\log x+(\log x)^2=(\log x)^2\Leftrightarrow 2+3\log x=0\Leftrightarrow \log x=-\frac{2}{3}\Leftrightarrow x=10^{-\frac{2}{3}}. \end{equation*} -
We use the fact that \(\sin 2x=2\sin x\cos x\) to obtain
\begin{equation*} \sin 2x-\sqrt{2}\cdot \sin x=0\Leftrightarrow 2\sin x\cos x-\sqrt{2}\cdot \sin x=0\Leftrightarrow \sin x\cdot (2\cos x-\sqrt{2})=0. \end{equation*}Hence
\begin{equation*} \sin 2x-\sqrt{2}\cdot \sin x=0\Leftrightarrow (\sin x=0 \text{ or } 2\cos x-\sqrt{2}=0). \end{equation*}Finally, we observe that since, \(x\in[0,2\pi )\text{,}\)
\begin{equation*} \sin x=0 \Leftrightarrow x=0 \text{ or } x=\pi \end{equation*}and
\begin{equation*} 2\cos x-\sqrt{2}=0\Leftrightarrow \cos x=\frac{\sqrt{2}}{2}\Leftrightarrow x=\frac{\pi}{4} \text{ or }x=\frac{7\pi}{4}. \end{equation*}Therefore, for \(x\in[0,2\pi )\text{,}\)
\begin{equation*} \sin 2x-\sqrt{2}\cdot \sin x=0\Leftrightarrow x\in \left\{0,\frac{\pi}{4},\pi, \frac{7\pi}{4}\right\}. \end{equation*}
Problem 5.3.6.
[8 marks] In this question use the fact that a tangent line to a circle at a point \(P\) on the circle is perpendicular to the line through \(P\) and the centre of the circle. See Figure 5.39
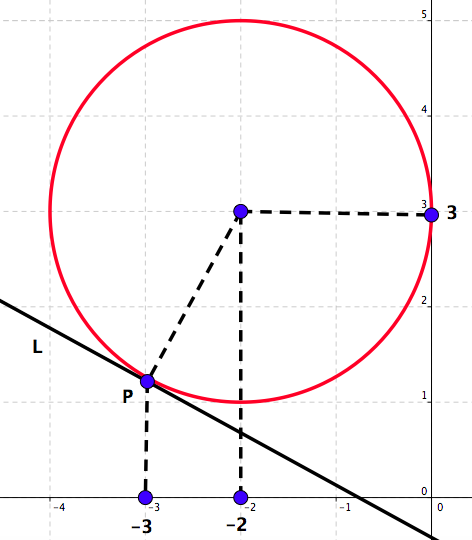
Find the equation of the circle in the diagram.
Find the coordinates of the point \(P\text{.}\)
Find the equation of the tangent line \(L\text{.}\)
-
We note that the centre of the circle is at the point \((-2,3)\) and that its radius is \(r=2\text{.}\) Hence the equation of the circle is
\begin{equation*} (x+2)^2+(y-3)^2=4. \end{equation*} -
The first coordinate of the point \(P\) is \(x=-3\text{.}\) We find the second coordinate, \(y\text{,}\) by using the fact that the point is on the circle:
\begin{equation*} (-3+2)^2+(y-3)^2=4\Leftrightarrow 1+(y-3)^2=4\Leftrightarrow (y-3)^2=3\Leftrightarrow y-3=\pm\sqrt{3}. \end{equation*}Since the point \(P\) is below the centre of the circle, it follows that \(y\lt 3\text{,}\) i.e \(y=3-\sqrt{3}\text{.}\) Hence, \(P=(-3,3-\sqrt{3})\text{.}\)
-
The line \(L\) is perpendicular to the line through \(P\) and the centre of the circle. Hence its slope is \(m=-\frac{1}{\sqrt{3}}\text{.}\)
The line is given by
\begin{equation*} y-(3-\sqrt{3})=-\frac{1}{\sqrt{3}}\cdot (x+3). \end{equation*}
Problem 5.3.7.
[8 marks] A farmer intends to work off a rectangular plot of land that will have an area of \(2000 \textrm{m}^2\text{.}\) The plot will be fenced and divided into two equal portions by an additional fence parallel to two sides. See Figure 5.40
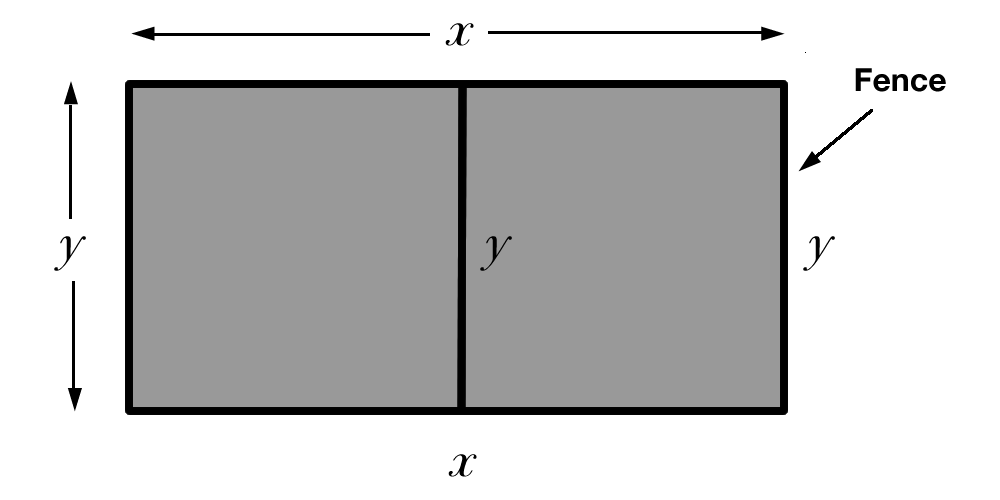
Find the total length \(L\) of fence used as a function of \(y\text{.}\) Classify the obtained function \(L=L(y)\) (i.e., determine if is this a linear function, a power function, a polynomial, a rational, an exponential, a logarithmic or a trigonometric function.)
What is the domain of the function \(L=L(y)\text{?}\)
Explain carefully what is that you can say about the total length \(L=L(y)\) of fence used if \(y\) is a large positive number. What if \(y\)is a small positive number?
Based on your answers in part (3) draw a rough sketch of the graph of the function \(L=L(y)\text{.}\) Is there a value of \(y\) that would yield the minimum length of the fence \(L\text{?}\)
-
The total length of the fence is given by \(L=2x+3y\text{.}\) From the fact that the area of the plot is \(2000 \textrm{m}^2\) we conclude that
\begin{equation*} 2000=xy\Rightarrow x=\frac{2000}{y}. \end{equation*}It follows that the total length \(L\) of fence used as a function of \(y\) is given by
\begin{equation*} L=L(y)=2\cdot \frac{2000}{y}+3y=\frac{4000}{y}+3y=\frac{4000+3y^2}{y}. \end{equation*}This is a rational function.
Since \(y\) represents the length of one side of the plot, we have that the domain of the function \(L=L(y)\) is the set of all positive real numbers, \((0,\infty )\text{.}\)
From \(L(y) = \frac{4000}{y}+3y\) we observe that if \(y\) is large then \(\frac{4000}{y}\) is small and \(L(y)\approx 3y\) is large. If \(y\) is small then \(L(y)\approx \frac{4000}{y}\) is large.
Observe that \(L(y)>0\) for \(y>0\) and that for \(y\) very large or very small, \(L(y)\) is very large. Hence the graph of the function \(L\) may look like one on Figure 5.41. The graph clearly suggests that there must be a value of\(y\) that will yield the minimum length of the fence \(L\text{.}\)
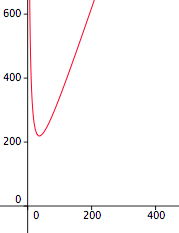
Figure 5.41. A rough sketch of graph of the function \(L\text{.}\)
Problem 5.3.8.
[7 marks] The first few so–called Bernoulli polynomials are given as follows:
It is known that the Bernoulli polynomials satisfy the following property: If \(h\) is such that \(|h|\) is a very small positive number then, for any real number \(x\) and any positive integer \(n\text{,}\)
-
Check the above fact for \(x=1\) and \(n=1\text{,}\) i.e. check that if \(|h|>0\) is small then
\begin{equation*} \frac{B_1(1+h)-B_1(1)}{h}\approx B_{0}(1). \end{equation*} -
Check the above fact for \(x=1\) and \(n=2\text{,}\) i.e. check that if \(|h|>0\) is small then
\begin{equation*} \frac{B_2(1+h)-B_2(1)}{h}\approx 2B_{1}(1). \end{equation*}
-
We note that, for \(|h|\not= 0\text{,}\)
\begin{equation*} \frac{B_1(1+h)-B_1(1)}{h}=\frac{(1+h)-\frac{1}{2}-(1-\frac{1}{2})}{h}=\frac{1+h-\frac{1}{2}-1+\frac{1}{2}}{h}=\frac{h}{h}=1=B_0(1). \end{equation*} -
From, for \(|h|\not= 0\text{,}\)
\begin{equation*} \begin{array}{rcl} \frac{B_2(1+h)-B_2(1)}{h}\amp =\amp \frac{(1+h)^2-(1+h)+\frac{1}{6}-(1^2-1+\frac{1}{6})}{h}\\ \amp =\amp \frac{1+2h+h^2-1-h+\frac{1}{6}-\frac{1}{6}}{h}\\ \amp =\amp \frac{1+2h+h^2-1-h}{h}=\frac{h(1+h)}{h}=1+h\\ \end{array} \end{equation*}and \(B_{1}(1)=1-\frac{1}{2}=\frac{1}{2}\) we conclude that, for a small value of \(|h|\not= 0\text{,}\)
\begin{equation*} \frac{B_2(1+h)-B_2(1)}{h}=1+h\approx 1=2\left(1-\frac{1}{2}\right)=2B_1(1). \end{equation*}
Problem 5.3.9.
[7 marks] Using the approximations \(\ln 2 \approx 0.6\) and \(\ln 5 \approx 1.6\) and the properties of logarithms, estimate each of the numbers below. Each question is worth \(1\) point – You have to show all your work, i.e. it must be clear which properties you are using.
Estimate \(\ln 8\text{.}\)
Estimate \(\ln 25\text{.}\)
Estimate \(\ln 10\text{.}\)
Estimate \(ln 2.5\text{.}\)
Estimate \(\ln 40\text{.}\)
Estimate \(\ln 50\text{.}\)
Estimate \(\log_2 5\text{.}\)
Observe, \(\ln 8=\ln (2^3)=3\ln 2\approx 3\cdot 0.6=1.8\text{.}\)
Observe, \(\ln 25=\ln (5^2)=2\ln 5\approx 2\cdot 1.6=3.2\text{.}\)
Observe, \(\ln 10=\ln (2\cdot 5)=\ln 2+\ln 5\approx 0.6+1.6=2.2\text{.}\)
Observe, \(ln 2.5=\ln \frac{25}{10}=\ln 25-\ln 10\approx 3.2-2.2=1\text{.}\)
Observe, \(\ln 40=\ln (8\cdot 5)=\ln 8+\ln 5\approx 1.8+1.6=3.4\text{.}\)
Observe, \(\ln 50=\ln (25\cdot 2)=\ln 25+\ln 2\approx 3.2+ 0.6=3.8\text{.}\)
-
Observe,
\begin{equation*} \log_25=\frac{\ln 5}{\ln 2}\approx \frac{1.6}{0.6}\approx 2.66\text{.} \end{equation*}
Problem 5.3.10.
[6 marks] Laura and Ali are standing 10m apart from each other, trying to read a sign which is some distance away from both of them. The angle formed by Ali's line of vision to the sign and his line of vision to Laura is \(\pi/6\text{.}\) The angle formed by Laura's line of vision to the sign and her line of vision to Ali is \(\pi/3\text{.}\) Find the distance between Laura and the sign.
Note that \(\frac{\pi}{3}+\frac{\pi}{6}=\frac{\pi}{2}\text{.}\) It follows that the third angle in the triangle with the vertices “Laura,” “Sign,” and “Ali” equals \(\frac{\pi}{2}\) and that this triangle is a right triangle with the right angle at the vertex “Sign” and the hypothenuse of the length \(10\text{.}\)
Let \(x\) be the distance between Laura and the sign, Then
See Figure 5.42
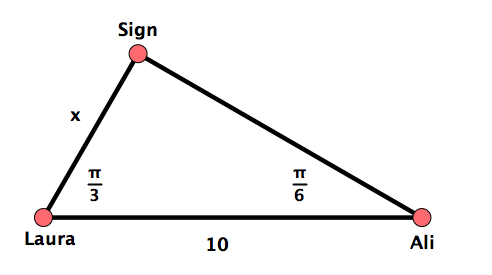
Problem 5.3.11.
[12 marks] Use the identities
to determine the exact values of each of the following numbers:
\(\cos \frac{\pi}{12}\text{.}\)
\(\sin \frac{7\pi}{12}\text{.}\)
\(\tan \frac{\pi}{12}\text{.}\)
\(\cot \frac{\pi}{12}\text{.}\)
-
Since \(\frac{\pi}{12}=\frac{\pi}{4}-\frac{\pi}{6}\text{,}\) it follows
\begin{equation*} \cos \frac{\pi}{12}=\cos \left( \frac{\pi}{4}-\frac{\pi}{6}\right)=\cos \frac{\pi}{4}\cos \frac{\pi}{6}+\sin \frac{\pi}{4}\sin \frac{\pi}{6}=\frac{\sqrt{2}}{2}\cdot\frac{\sqrt{3}}{2}+\frac{\sqrt{2}}{2}\cdot\frac{1}{2}=\frac{\sqrt{6}+\sqrt{2}}{4}. \end{equation*} -
Since \(\frac{7\pi}{12}=\frac{\pi}{2}+\frac{\pi}{12}\text{,}\) it follows
\begin{equation*} \sin \frac{7\pi}{12}=\sin \left( \frac{\pi}{2}+\frac{\pi}{12}\right)=\sin \frac{\pi}{2}\cos \frac{\pi}{12}+\cos \frac{\pi}{2}\sin \frac{\pi}{12}=1\cdot\frac{\sqrt{6}+\sqrt{2}}{4}+0\cdot\sin \frac{\pi}{12}=\frac{\sqrt{6}+\sqrt{2}}{4}. \end{equation*} -
By definition, \(\tan \frac{\pi}{12}=\frac{\sin \frac{\pi}{12}}{\cos \frac{\pi}{12}}\text{.}\)
From \(\cos \frac{\pi}{12}=\frac{\sqrt{6}+\sqrt{2}}{4}\) it follows
\begin{equation*} \sin^2\left( \frac{\pi}{12}\right)=1-\cos^2\left(\frac{\pi}{12}\right)=1-\left(\frac{\sqrt{6}+\sqrt{2}}{4}\right)^2=1-\frac{6+2\sqrt{12}+2}{16} \end{equation*}\begin{equation*} =1-\frac{8+4\sqrt{3}}{16}=1-\frac{2+\sqrt{3}}{4}=\frac{4-2-\sqrt{3}}{4}=\frac{2-\sqrt{3}}{4}. \end{equation*}\begin{equation*} =\frac{3-2\sqrt{3}+1}{8}=\frac{(\sqrt{3}-1)^2}{8}. \end{equation*}Next we note that \(\frac{\pi}{12}\in\left(0,\frac{\pi}{2}\right)\) which implies that
\begin{equation*} \sin \frac{\pi }{12}=\sqrt{\frac{(\sqrt{3}-1)^2}{8}}=\frac{\sqrt{3}-1}{2\sqrt{2}}=\frac{\sqrt{6}-\sqrt{2}}{4}\gt 0. \end{equation*}Finally,
\begin{equation*} \tan \frac{\pi}{12}=\frac{\sin \frac{\pi}{12}}{\cos \frac{\pi}{12}}=\frac{\frac{\sqrt{6}-\sqrt{2}}{4}}{\frac{\sqrt{6}+\sqrt{2}}{4}}=\frac{\sqrt{6}-\sqrt{2}}{\sqrt{6}+\sqrt{2}} \end{equation*} By definition, \(\cot \frac{\pi}{12}=\frac{1}{\tan \frac{\pi }{12}}=\frac{\sqrt{6}+\sqrt{2}}{\sqrt{6}-\sqrt{2}}\text{.}\)
Problem 5.3.12.
[6 marks] A function\(f:\left[-\frac{\pi}{2},\frac{\pi}{2}\right]\to [-1,1]\) is given by \(f(x)=\sin x\text{,}\) for all \(x\in\left[-\frac{\pi}{2},\frac{\pi}{2}\right]\text{.}\) See Figure 5.43
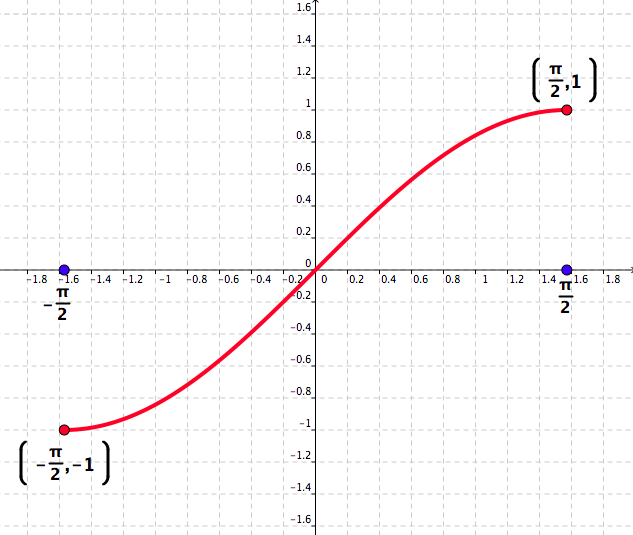
Justify the fact that the function \(f\) has an inverse, i.e. justify the fact that the function \(f^{-1}\) exists. The function \(f^{-1}\) is called the inverse sine function and it is denoted by \(f^{-1}(x)=\sin^{-1}x\text{.}\)
State the domain and range of the function \(f^{-1}\text{.}\)
Draw a graph of the function \(f^{-1}\text{.}\)
We observe that the graph of the function \(f\) passes the horizontal line test, i.e. each horizontal line intersects the graph of \(f\) at most one point. Hence, the function \(f\) is one–to–one, which implies that \(f\) has an inverse.
Since \(f:\left[-\frac{\pi}{2},\frac{\pi}{2}\right]\to [-1,1]\) we have that \(f^{-1}:[-1,1]\to \left[-\frac{\pi}{2},\frac{\pi}{2}\right]\text{.}\) Therefore, the domain of the function \(f^{-1}\) is the segment \([-1,1]>\) and its range is the segment \(\left[-\frac{\pi}{2},\frac{\pi}{2}\right]\text{.}\)
-
See Figure 5.44

Figure 5.44. \(f^{-1}(x)=\arcsin x\text{,}\) \(x\in[-1,1]\)
Problem 5.3.13.
[10 marks] Sketch graphs of the following functions: