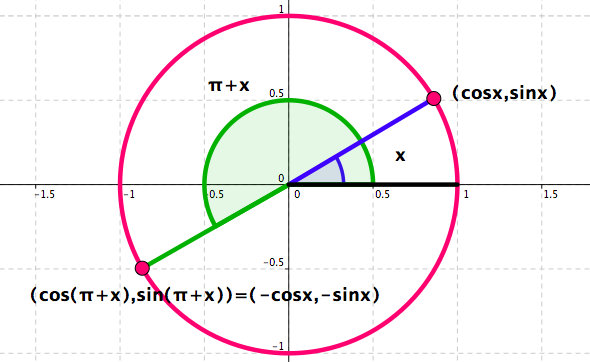Section 4.5 Trigonometric Identities
I want the circle
broken.
From the poem “The circle game.” — Margaret Atwood, Canadian poet, novelist, literary critic, and essayist, 1939–
Problem: Evaluate \(\cos \frac{\pi}{12}\text{.}\)
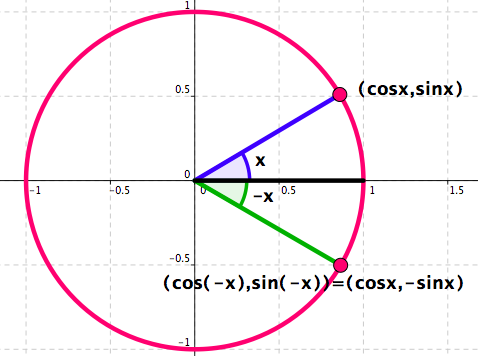
Trigonometric Identities - Some are obvious. See Figure 4.55 .
Figure 4.55. Recall how \(x\mapsto \cos x\) and \(x\mapsto \sin x\) are defined. For any real number \(x\text{:}\)
\begin{equation*}
\cos^2x+\sin^2x=1
\end{equation*}
\begin{equation*}
\cos(-x)=\cos(x)
\end{equation*}
\begin{equation*}
\sin(-x)=-\sin(x)
\end{equation*}
Example 4.5.1 . Given \(\sin x\) find \(\cos x\).
If \(x\in\left( \frac{\pi}{2},\pi\right)\) and \(\sin x=\frac{1}{3}\text{,}\) find \(\cos x\text{.}\)
Solution
From \(\cos^2x+\sin^2x=1\) it follows that
\begin{equation*}
\cos^2x=1-\sin^2x=1-\left(\frac{1}{3}\right)^2=1-\frac{1}{9}=\frac{8}{9}.
\end{equation*}
Note that
\begin{equation*}
x\in\left( \frac{\pi}{2},\pi\right)\Rightarrow \cos x\lt 0.
\end{equation*}
We conclude that
\begin{equation*}
\cos x=-\sqrt{\frac{8}{9}}=-\frac{2\sqrt{2}}{3}.
\end{equation*}
Example 4.5.2 . Prove identity.
Prove that any real number \(x\) such that \(x\not= \frac{\pi}{2}+k\pi\text{,}\) \(k\in \mathbb{Z}\text{:}\)
\begin{equation*}
\tan ^2x+1=\sec^2x.
\end{equation*}
Solution
Observe that
\begin{equation*}
tan ^2x+1=\left(\frac{\sin x}{\cos x}\right)^2+1=\frac{\sin ^2x}{\cos^2x}+1=\frac{\sin^2+\cos^2x}{\cos^2x}=\frac{1}{\cos^2x}=\sec^2x.
\end{equation*}
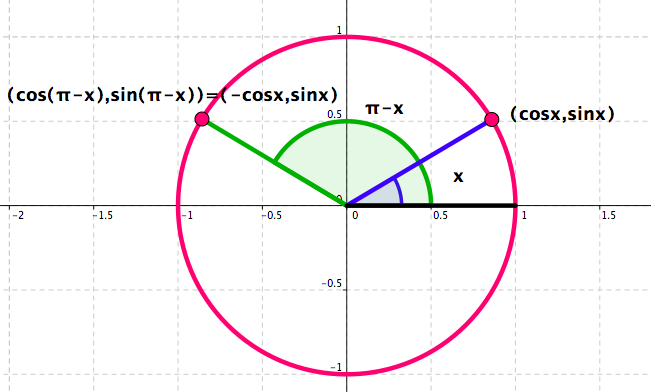
Trigonometric Identities - Some are easy to see. See Figure 4.56 and Figure 4.57 .
Figure 4.56. Recall how \(x\mapsto \cos x\) and \(x\mapsto \sin x\) are defined.Figure 4.57. Recall how \(x\mapsto \cos x\) and \(x\mapsto \sin x\) are defined. For any real number \(x\text{:}\)
\begin{equation*}
\cos(\pi+x)=-\cos x
\end{equation*}
\begin{equation*}
\sin(\pi+x)=-\sin x
\end{equation*}
\begin{equation*}
\cos(\pi-x)=-\cos )
\end{equation*}
\begin{equation*}
\sin(\pi-x)=-\sin x
\end{equation*}
Example 4.5.3 . Supplementary angles.
Use the fact that
\begin{equation*}
\cos \frac{\pi}{12}=\frac{\sqrt{2+\sqrt{3}}}{2}
\end{equation*}
to find \(\sin \frac{11\pi}{12}\text{.}\)
Solution
Note that \(\frac{11\pi}{12}=\pi-\frac{\pi}{12}\text{.}\)
It follows that
\begin{equation*}
\sin \frac{11\pi}{12}=\sin\left(\pi-\frac{\pi}{12}\right)=\sin \frac{\pi}{12}.
\end{equation*}
From the fact that, for any \(x\in \mathbb{R}\text{,}\) \(\sin^2x+\cos^2x=1\text{,}\) it follows that
\begin{equation*}
\sin^2 \frac{\pi}{12}=1-\cos^2 \frac{\pi}{12}=1-\left(\frac{\sqrt{2+\sqrt{3}}}{2}\right)^2=1-\frac{2+\sqrt{3}}{4}=\frac{4-(2+\sqrt{3})}{4}=\frac{2-\sqrt{3}}{4}.
\end{equation*}
Since \(\frac{\pi}{12} \in \left( 0,\frac{\pi}{2}\right)\) it follows that \(\displaystyle \sin \frac{\pi}{12}>0\) so we conclude that
\begin{equation*}
\sin \frac{\pi}{12}=\sqrt{\frac{2-\sqrt{3}}{4}}=\frac{\sqrt{2-\sqrt{3}}}{2}.
\end{equation*}
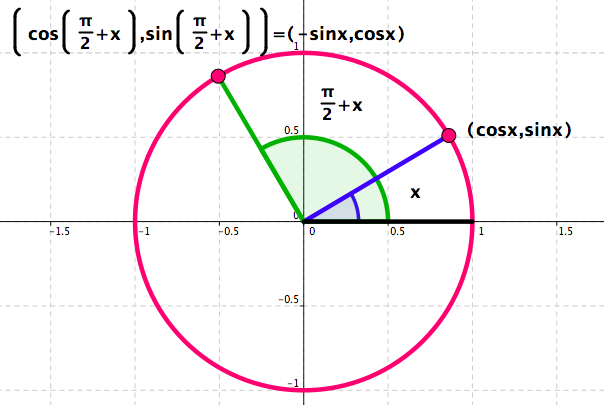
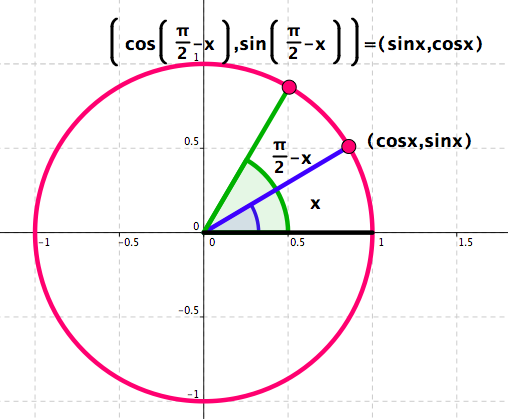
Trigonometric Identities - Some need a bit of thinking. See Figure 4.58 and Figure 4.59 .
Figure 4.58. Recall how \(x\mapsto \cos x\) and \(x\mapsto \sin x\) are defined.Figure 4.59. Recall how \(x\mapsto \cos x\) and \(x\mapsto \sin x\) are defined. For any real number \(x\text{:}\)
\begin{equation*}
\cos\left(\frac{\pi}{2}+x\right)=-\sin x
\end{equation*}
\begin{equation*}
\sin\left(\frac{\pi}{2}+x\right)=\cos x
\end{equation*}
\begin{equation*}
\cos\left(\frac{\pi}{2}-x\right)=\sin x
\end{equation*}
\begin{equation*}
\sin\left(\frac{\pi}{2}-x\right)=\cos x
\end{equation*}
Example 4.5.4 . Complementary angles.
Use the fact that
\begin{equation*}
\cos \frac{\pi}{12}=\frac{\sqrt{2+\sqrt{3}}}{2}
\end{equation*}
to find \(\cos \frac{7\pi}{12}\text{.}\)
Solution
Note that \(\frac{7\pi}{12}=\frac{\pi}{2}+\frac{\pi}{12}\text{.}\)
It follows that
\begin{equation*}
\cos \frac{7\pi}{12}=\cos\left(\frac{\pi}{2}+\frac{\pi}{12}\right)=-\sin \frac{\pi}{12}=-\frac{\sqrt{2-\sqrt{3}}}{2}.
\end{equation*}
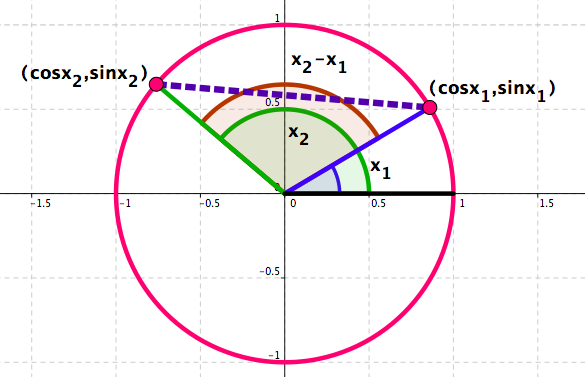
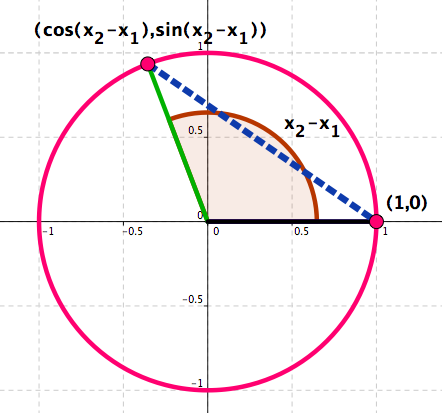
Trigonometric Identities - Some need a bit more of thinking. See Figure 4.60 .
Figure 4.60. The distance between the points \((\cos x_2,\sin x_2)\) and \((\cos x_1,\sin x_1)\) is equal to the distance between the points \((\cos (x_2-x_1),\sin (x_2-x_1))\) and \((1,0)\text{.}\) From
\begin{equation*}
\color{red}{\text{Distance}\{}(\cos x_2,\sin x_2),(\cos x_1,\sin x_1)\color{red}{\}}=\color{red}{\text{Distance }\{}(\cos (x_2-x_1),\sin (x_2-x_1)),(1,0)\color{red}{\}}
\end{equation*}
it follows
\begin{equation*}
(\cos x_2-\cos x_1)^2+(\sin x_2-\sin x_1)^2=(\cos (x_2-x_1)-1)^2+(\sin (x_2-x_1)-0)^2.
\end{equation*}
Hence
\begin{equation*}
\cos^2x_2-2\cos x_2\cos x_1+\cos^2x_1+\sin^2x_2-2\sin x_2\sin x_1+\sin^2x_1
\end{equation*}
\begin{equation*}
=\cos^2(x_2-x_1)-2\cos (x_2-x_1)+1+\sin^2 (x_2- x_1).
\end{equation*}
Next, observe
\begin{equation*}
\color{red}{(}\cos^2x_2+\sin^2x_2\color{red}{)}+ \color{red}{(}\cos^2x_1+\sin^2x_1\color{red}{)}-2(\cos x_2\cos x_1+\sin x_2\sin x_1)
\end{equation*}
\begin{equation*}
=\color{red}{(}\cos^2(x_2-x_1)+\sin^2 (x_2- x_1)\color{red}{)}+1-2\cos (x_2-x_1)
\end{equation*}
\begin{equation*}
1+1-2(\cos x_2\cos x_1+\sin x_2\sin x_1)=1+1-2\cos (x_2-x_1)
\end{equation*}
\begin{equation*}
-2(\cos x_2\cos x_1+\sin x_2\sin x_1)=-2\cos (x_2-x_1)
\end{equation*}
\begin{equation*}
\cos x_2\cos x_1+\sin x_2\sin x_1=\cos (x_2-x_1)
\end{equation*}
MUST KNOW! MUST MEMORIZE! For any real number \(x\text{:}\)
\begin{equation*}
\cos(x_1-x_2)=\cos x_1\cos x_2+\sin x_1\sin x_2
\end{equation*}
\begin{equation*}
\cos(x_1+x_2)=\cos x_1\cos x_2-\sin x_1\sin x_2
\end{equation*}
\begin{equation*}
\sin(x_1-x_2)=\sin x_1\cos x_2-\cos x_1\sin x_2
\end{equation*}
\begin{equation*}
\sin(x_1+x_2)=\sin x_1\cos x_2+\cos x_1\sin x_2
\end{equation*}
Example 4.5.5 . Use what you know to get what you don't.
Evaluate \(\cos \frac{\pi}{12}\text{.}\)
Solution
Note that \(\frac{\pi}{12}=\frac{\pi}{3}-\frac{\pi}{4}\text{.}\)
It follows that
\begin{equation*}
\cos \frac{\pi}{12}=\cos\left(\frac{\pi}{3}-\frac{\pi}{4}\right)=\cos\frac{\pi}{3}\cos\frac{\pi}{4}+\sin\frac{\pi}{3}\sin\frac{\pi}{4}=\frac{1}{2}\cdot\frac{\sqrt{2}}{2}+\frac{\sqrt{3}}{2}\cdot\frac{\sqrt{2}}{2}=\frac{\sqrt{2}(1+\sqrt{3})}{4}.
\end{equation*}
Note: In Example 4.58 we were given that
\begin{equation*}
\cos \frac{\pi}{12}=\frac{\sqrt{2+\sqrt{3}}}{2}.
\end{equation*}
Note
\begin{equation*}
\frac{\sqrt{2}(1+\sqrt{3})}{4}=\frac{\sqrt{2+\sqrt{3}}}{2}\Leftrightarrow \sqrt{2}(1+\sqrt{3})=2\sqrt{2+\sqrt{3}}\Leftrightarrow 2\cdot(1+\sqrt{3})^2=4(2+\sqrt{3}).
\end{equation*}
\begin{equation*}
\Leftrightarrow 2\cdot(1+2\sqrt{3}+3)=8+4\sqrt{3}\Leftrightarrow 2\cdot(4+2\sqrt{3})=8+4\sqrt{3}
\end{equation*}
which is true.
Trigonometric Identities – Some follow from what we already know.
\(\displaystyle \sin 2x=2\sin x\cos x\)
Solution
Note
\begin{equation*}
\sin 2x=\sin (x+x)=\sin x\cos x+\cos x\sin x=2\sin x\cos x.
\end{equation*}
\(\displaystyle \cos 2x=\cos^2x-\sin^2x\)
Solution
Note
\begin{equation*}
\cos 2x=\cos (x+x)=\cos x\cos x-\sin x\sin x=\cos^2 x-\sin^2x.
\end{equation*}
\(\displaystyle \cos^2x=\frac{1+\cos 2x}{2}\)
Solution
From
\begin{equation*}
1=\cos^2x+\sin^2x \text{ and }\cos 2x=\cos^2x-\sin^2x
\end{equation*}
it follows that
\begin{equation*}
1+\cos 2x=(\cos^2x+\sin^2x)+(\cos^2x-\sin^2x)=2\cos^2x.
\end{equation*}
Thus
\begin{equation*}
\cos^2x=\frac{1+\cos 2x}{2}.
\end{equation*}
\(\displaystyle \sin^2x=\frac{1-\cos 2x}{2}\)
Solution
From
\begin{equation*}
1=\cos^2x+\sin^2x \text{ and }\cos 2x=\cos^2x-\sin^2x
\end{equation*}
it follows that
\begin{equation*}
1-\cos 2x=(\cos^2x+\sin^2x)-(\cos^2x-\sin^2x)=2\sin^2x.
\end{equation*}
Thus
\begin{equation*}
\sin^2x=\frac{1-\cos 2x}{2}.
\end{equation*}
\(\displaystyle \cos \frac{x}{2}=\pm \sqrt{\frac{1+\cos x}{2}}\)
Solution
Observe that \(\displaystyle x=2\cdot \frac{x}{2}\text{.}\)
Next, note that by the identity (3) from above
\begin{equation*}
\cos^2 \frac{x}{2}=\frac{1+\cos \left(2\cdot \frac{x}{2}\right)}{2}=\frac{1+\cos x}{2}.
\end{equation*}
Thus
\begin{equation*}
\cos \frac{x}{2}=\pm \sqrt{\frac{1+\cos 2x}{2}}.
\end{equation*}
To decide which sign you need (“\(+\)” or “\(-\)”) you have to find to which quadrant the angle \(\frac{x}{2}\) belongs to.
\(\displaystyle \sin\frac{x}{2}=\pm \sqrt{\frac{1-\cos x}{2}}\)
Solution
Observe that \(\displaystyle x=2\cdot \frac{x}{2}\text{.}\)
Next, note that by the identity (4) from above
\begin{equation*}
\sin^2 \frac{x}{2}=\frac{1-\cos \left(2\cdot \frac{x}{2}\right)}{2}=\frac{1-\cos x}{2}.
\end{equation*}
Thus
\begin{equation*}
\sin \frac{x}{2}=\pm \sqrt{\frac{1-\cos 2x}{2}}.
\end{equation*}
To decide which sign you need (“\(+\)” or “\(-\)”) you have to find to which quadrant the angle \(\frac{x}{2}\) belongs to.
Example 4.5.6 . Everything together.
Determine \(\cos \frac{7\pi}{8}\text{,}\) \(\sin \frac{7\pi}{8}\text{,}\) and \(\tan \frac{7\pi}{8}\)
Solution
Observe that \(\frac{\pi}{2}\lt \frac{7\pi}{8}\lt \pi\text{.}\)
This implies
\begin{equation*}
\cos \frac{7\pi}{8}\lt 0 \text{ and } \sin \frac{7\pi}{8}\gt 0.
\end{equation*}
Next, note that
\begin{equation*}
\frac{7\pi}{8}=\frac{1}{2}\cdot \frac{7\pi}{4}.
\end{equation*}
By the identity (5) and the fact that the angle is in the second quadrant we conclude
\begin{equation*}
\cos \frac{7\pi}{8}=-\sqrt{\frac{1+\cos\frac{7\pi}{4}}{2}}=-\sqrt{\frac{1+\frac{\sqrt{2}}{2}}{2}}=-\sqrt{\frac{2+\sqrt{2}}{4}}=-\frac{\sqrt{2+\sqrt{2}}}{2}.
\end{equation*}
Similarly,
\begin{equation*}
\sin \frac{7\pi}{8}=\sqrt{\frac{1-\cos\frac{7\pi}{4}}{2}}=\sqrt{\frac{1-\frac{\sqrt{2}}{2}}{2}}=\sqrt{\frac{2-\sqrt{2}}{4}}=\frac{\sqrt{2-\sqrt{2}}}{2}.
\end{equation*}
It follows that
\begin{equation*}
\tan \frac{7\pi}{8}=\frac{\sin \frac{7\pi}{8}}{\cos \frac{7\pi}{8}}=\frac{\frac{\sqrt{2-\sqrt{2}}}{2}}{-\frac{\sqrt{2+\sqrt{2}}}{2}}=-\frac{\sqrt{2-\sqrt{2}}}{\sqrt{2+\sqrt{2}}}=-\sqrt{\frac{2-\sqrt{2}}{2+\sqrt{2}}}.
\end{equation*}
We can further simplify the last expression by rationalizing the denominator, i.e. by getting rid of all radicals that are in the denominator. This idea is based on the following fact (called “the difference of squares”)
\begin{equation*}
(a+b)(a-b)=a^2-b^2.
\end{equation*}
Thus
\begin{equation*}
\frac{2-\sqrt{2}}{2+\sqrt{2}}=\frac{2-\sqrt{2}}{2+\sqrt{2}}\cdot \frac{2-\sqrt{2}}{2-\sqrt{2}}=\frac{(2-\sqrt{2})^2}{4-2}=\frac{(2-\sqrt{2})^2}{2}.
\end{equation*}
Finally,
\begin{equation*}
\tan \frac{7\pi}{8}=-\sqrt{\frac{2-\sqrt{2}}{2+\sqrt{2}}}=-\sqrt{\frac{(2-\sqrt{2})^2}{2}}=-\frac{2-\sqrt{2}}{\sqrt{2}}=-(\sqrt{2}-1)=1-\sqrt{2}.
\end{equation*}