Section 4.4 Trigonometry In Right Triangle
The Bermuda Triangle got tired of warm weather. It moved to Alaska. Now Santa Claus is missing. — Steven Alexander Wright, American comedian, actor, writer, and an Oscar-winning film producer, 1955 –
Problem: Evaluate \(x\) and \(y\text{.}\) See Figure 4.48.
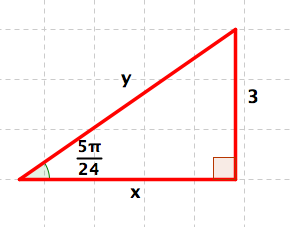
Reminder. We say that two triangles are similar if two angles of one triangle have measures equal to the measures of two angles of the other triangle. See Figure 4.49.
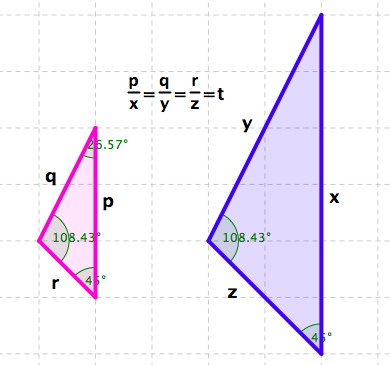
Similar Right Triangles: See Figure 4.50.
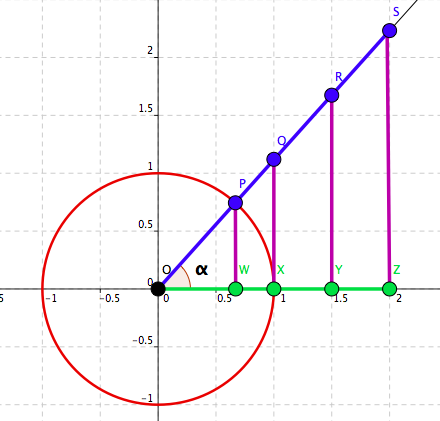
Right Triangle and Trigonometric Functions: Let \(\alpha \in \left(0,\frac{\pi}{2}\right)\) be an angle in a right triangle. See Figure 4.51.
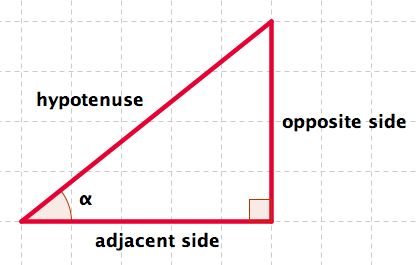
Then:
Example 4.4.1. Given sides evaluate trigonometric functions.
Evaluate \(\cos \alpha\text{,}\) \(\sin \alpha\text{,}\) \(\tan \alpha\text{,}\) \(\cot \alpha\text{,}\) \(\sec \alpha\text{,}\) and \(\csc \alpha\text{.}\) See Figure 4.52.
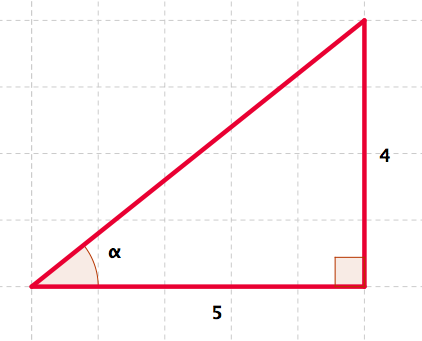
Note that \(\text{adjacent side}=5\text{,}\) \(\text{opposite side}=4\text{,}\) and, by the Pythagorean theorem, \(\text{hypothenuse}=\sqrt{4^2+5^2}=\sqrt{41}\text{.}\)
By definition:
Example 4.4.2. Given angle and a side evaluate other sides.
Evaluate \(x\) and \(y\text{.}\) See Figure 4.53.

Observe that
and
Example 4.4.3. A Summer Day in British Columbia.
It is a beautiful summer day and you and your visitor from Toronto, ON, are kayaking through Howe Sound, a network of fjords situated northwest of Vancouver, B.C.
“This is The Stawamus Chief,” you inform your friend. “It is the second largest granite monolith in the world. For the Squamish nation The Chief is an important spiritual place. A Squamish legend says that it is a longhouse that spirit–beings turned into stone.”.
“Wow,” you hear your friend exclaim. “I wonder what the elevation of the highest point is.”
“Well, we are about 1200 metres away from the shore and I'd estimate that the angle of elevation is about \(\frac{\pi}{6}\) so …”
See Figure 4.54.
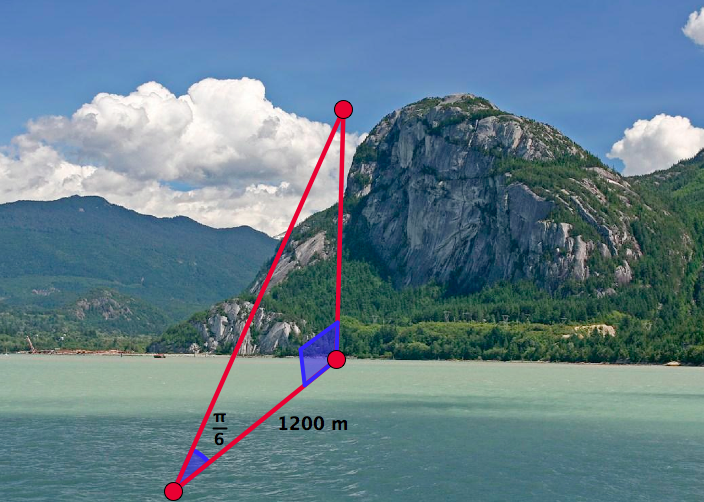
Observe that the elevation of the highest point \(H\) matches the opposite side to the angle \(\frac{\pi}{6}\) in the (red) right triangle. Hence
Note: The actual elevation is 702 meters.
