Section 46.2 Combinatorial Geometry
Problem 46.2.1.
Let us \(3\)–colour the points of the plane. Prove that there will be two points at distance \(1\) with the same colour.
We \(3\)–colour the points of the plane and throw the Moser spindle in the plane. There must be two points at distance \(1\) with the same colour.
Problem 46.2.2.
We \(2\)–colour the points of the plane. Suppose that there are three points of the same colour forming a regular (equilateral) triangle with side 1 (a monochromatic regular triangle with side 1, for short). Then for each \(a,b\gt 0\) such that \(|a-b| \lt 1 \lt a+b\text{,}\) we have a monochromatic triangle with sides \(1, a, b\text{.}\)
Suppose that \(\triangle ABC\) is red regular triangle with side 1.
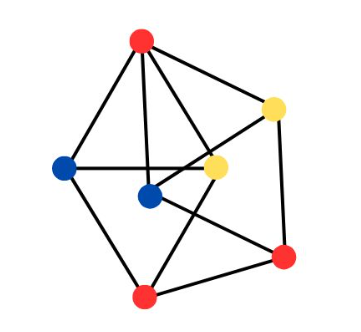
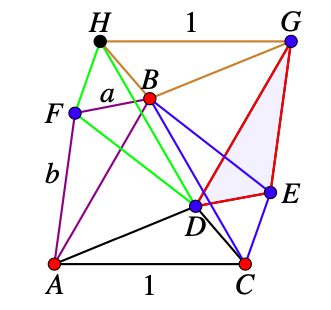
Consider the set of points \(\{D,E,F,G,H\}\) so that \(\triangle ACD\text{,}\) \(\triangle ABF\text{,}\) \(\triangle BDF\text{,}\) \(\triangle BCE\text{,}\) \(\triangle BGH\text{,}\) and \(\triangle DFH\) be six mutually congruent triangles with sides \(1, a, b\text{.}\)
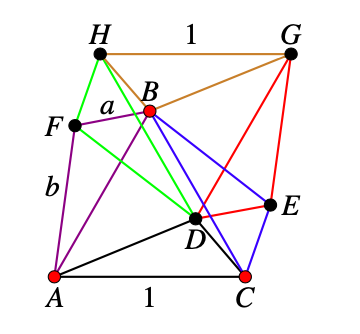
If any of the vertices \(D,F\) or \(E\) is red the then one of \(\triangle ACD\text{,}\) \(\triangle ABF\text{,}\) or \(\triangle BCE\) is a red triangle with sides \(1, a, b\text{.}\)
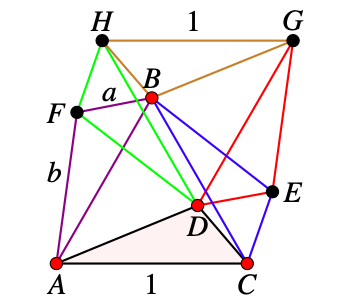
Suppose that \(D,F\) and \(E\) are blue.
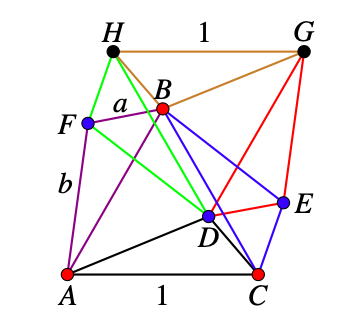
If both \(G\) and \(H\) are red then \(\triangle BHG\) is a red triangle with sides \(1, a, b\text{.}\)
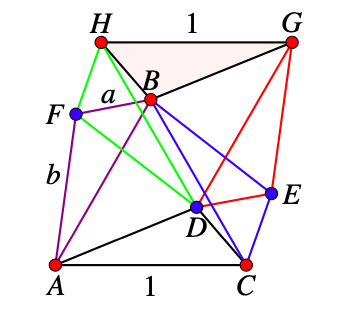
If one of \(G\) or \(H\) is blue then there is a blue triangle with sides \(1, a, b\text{.}\)
Problem 46.2.3.
Show that if we \(2\)–colour the points of the plane, then we do not necessarily have a monochromatic regular triangle with side 1.
Prove that in any \(2\)–colouring of the points of the plane, we always have a monochromatic triangle with sides \(\sqrt{2}\text{,}\) \(\sqrt{6}\text{,}\) and \(\pi\text{.}\)
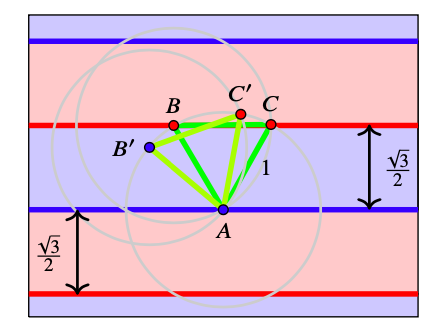
We cover the plane with stripes of width \(\frac{\sqrt{3}}{2}\text{,}\) that alternate in the colours, red and blue. Each strip includes its lower edge. It is not difficult to see that any equilateral triangle with the side 1 thrown in such a plane will have exactly two vertices of the same colour.
We consider \(1\text{, }\sqrt{3}\text{, }\frac{\pi}{\sqrt{2}}\) since we can obtain the case in the statement of the problem by multiplying each of them by \(\frac{1}{\sqrt{2}}\text{.}\)
Our strategy is to prove that any \(2\)–colouring of the points of the plane, yields a monochromatic triangle with sides \(1\) or \(\sqrt{3}\text{.}\) Since \(\frac{\pi}{\sqrt{2}}-\sqrt{3}\lt 1\lt\frac{\pi}{\sqrt{2}}+\sqrt{3}\) and \(\frac{\pi}{\sqrt{2}}-1\lt \sqrt{3}\lt\frac{\pi}{\sqrt{2}}+1\text{,}\) by Problem 46.2.2, there must exist a monochromatic triangle with sides \(1\text{, }\sqrt{3}\text{, }\frac{\pi}{\sqrt{2}}\text{.}\)
Suppose that a \(2\)– colouring uses both colours.
We suppose that \(A\) is red and that \(B\) is coloured blue and that the distance between them is \(2\text{.}\)Observe that if \(A\) and \(B\) are of different colours then, since we can connect them by a polygonal line with sides \(2\text{,}\) there are two points with different colours and at the distance \(2\text{.}\)
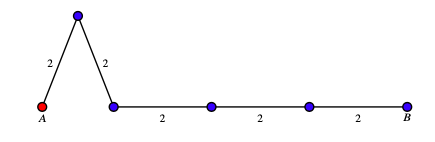
Suppose that the point \(C\) is red. If one of the points \(D\) or \(E\) is red, then there is a red-monochromatic equilateral triangle of side \(1\text{.}\) If both \(D\) and \(E\) are blue then \(\triangle BDE\) is a monochromatic equilateral triangle of side \(\sqrt{3}\text{.}\)
Let \(C\) the midpoint of the line segment \(\overline{AB}\text{.}\) We consider two more points, \(D\) and \(E\text{,}\) so that \(|\overline{AD}|=\overline{AE}=1\text{,}\) \(|\overline{BD}|=\overline{BE}=\sqrt{3}\text{,}\) and \(|\overline{CD}|=\overline{CE}=1\text{.}\) We obtain the graph depicted in the figure. .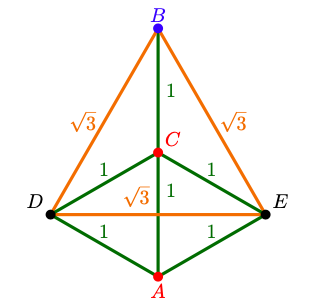
Problem 46.2.4.
Does there exist a natural number \(n=n_{0}(k,R)\) such that, if we \(k\)–colour the points of the \(n\)–dimensional Euclidean space, one of the colours will contain a configuration congruent to \(R\text{,}\) where (a) \(R\) is a rectangle; and (b) \(R\) is a non–rectangular parallelogram.
(a) Let \(a\gt 0\) and \(b\gt 0\) be the lengths of edges of the rectangle \(R\) and let \(N=k^{k+1}\text{.}\)
Let \(v_0,\ldots,v_N\) be the vertices of a regular simplex in the \(N\)–dimensional space with side length \(a\) and let \(w_0,\ldots,w_k\) be the vertices of a regular simplex in the \(k\)–dimensional space with side length \(b\text{.}\)
Observe that the set
is a set of points in the \((N+k)\)–dimensional space. Also observe that for each fixed \(i\text{,}\) the set \((k+1)\)–element set \(P_i=\{(v_i,w_j):0\leq j\leq k\}\) can be coloured in \(k^{k+1}=N\) ways.
Let \(c\) be a \(k\)–colouring of the \((N+k)\)–dimensional space. For each \(0\leq 0\leq i\leq N\text{,}\) let \(c_i\) be a \(k\)–colouring of the \((k+1)\)–element set \(\{w_0,\ldots,w_k\}\) defined by \(c_i(w_j)=c(v_i,w_j)\text{.}\)
Since each of the \(N+1\) sets \(P_i\) can be coloured in \(N\) ways, by the Pigeonhole Principle there are \(0\leq i_1\lt i_2\leq N\) such that \(c_{i_1}=c_{i_2}\text{,}\) i.e., such that \(c(v_{i_1},w_j)=c(v_{i_2},w_j)\) for each \(0\leq j\leq k\text{.}\) Since \(c\) is a \(k\)–colouring and since the set \(\{0,1,\ldots,k\}\) has \(k+1\) elements, by the Pigeonhole Principle, there are \(0\leq j_1\lt j_2\leq k\) such that \(c(v_{i_1},w_{j_1})=c(v_{i_1},w_{j_2})=c(v_{2_1},w_{j_2})=c(v_{i_2},w_{j_1})\text{.}\) Hence, there are four points, \((v_{i_1},w_{j_1})\text{,}\) \((v_{i_1},w_{j_2})\text{,}\) \((v_{i_2},w_{j_1})\) and \((v_{i_2},w_{j_2})\text{,}\) which form a monochromatic rectangle, that is congruent to \(R\text{.}\)
(b) Let \(\mathbf{a}\) and \(\mathbf{b}\) be two side vectors of the parallelogram \(R\text{.}\) Since \(R\) is non–rectangular, \(\mathbf{a}\cdot \mathbf{b}\neq 0\text{.}\) Let \(\mathbf{a}\cdot\mathbf{b}=1\text{.}\) We claim the Ramsey number \(n(4,R)\) does not exist.
Let \(n\in \mathbb{N}\)
Let \(c\) be a \(4\)–colouring of the \(n\)–dimensional Euclidean space defined, for \(\mathbf{w} \in E^n\) and \(i\in\{0,1,2,3\}\text{,}\)
We claim there is no \(c\)–monochromatic set congruent to \(R\text{.}\)
Suppose by contradiction that there is such a set \(R^\prime\text{,}\) then \(R'=\{\mathbf{w},\mathbf{w}+\mathbf{a'},\mathbf{w}+\mathbf{b'},\mathbf{w}+\mathbf{a'}+\mathbf{b'}\}\text{,}\) where \(\mathbf{a'},\mathbf{b'}\in E^n\text{.}\) Since this set is monochromatic, it follows that
i.e., it follows that
On the other hand, since for some \(\theta_1,\theta_2,\theta_3,\theta_4\in[0,1)\text{,}\) \(\lfloor \mathbf{w}^2\rfloor=\mathbf{w}^2-\theta_1\text{,}\) \(\lfloor (\mathbf{w}+\mathbf{a'})^2\rfloor=(\mathbf{w}+\mathbf{a'})^2-\theta_2\text{,}\) \(\lfloor (\mathbf{w}+\mathbf{b'})^2\rfloor=(\mathbf{w}+\mathbf{b'})^2\theta_3\text{,}\) and \(\lfloor(\mathbf{w}+\mathbf{a'}+\mathbf{b'})^2\rfloor=\mathbf{w}+\mathbf{a'}+\mathbf{b'})^2-\theta_4\text{,}\) it follows that
where \(\Theta=\theta_1-\theta_2-\theta_3+\theta_4\in (-2,2)\text{.}\)
Since we assume \(\mathbf{a}\cdot\mathbf{b}=1\text{,}\) \(2\mathbf{a'}\cdot\mathbf{b'}+\Theta=2+\Theta\in(-4,4)\) is not divisible by 4.
Thus, there is no \(c\)–monochromatic set that is congruent to \(R\text{.}\)
