Processing math: 100%
Skip to main content
Section 17.3 Implementation
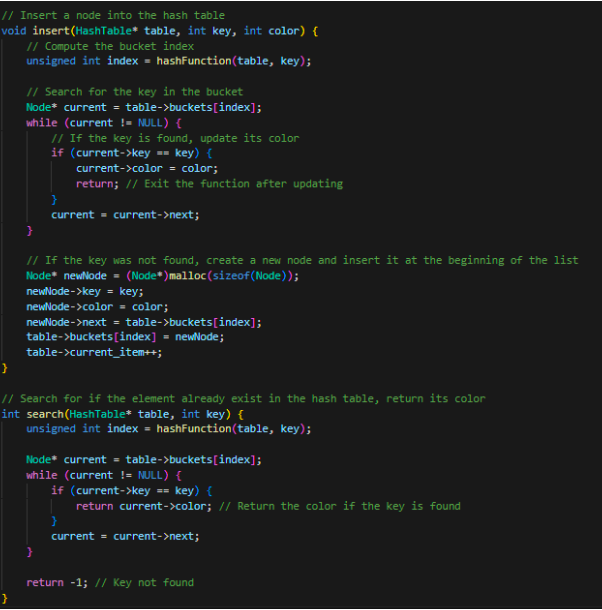
In this part, I will describe my process on implementing the program, how and what did I implement in order to make it work and the execution flow of the program. The data structure that I have decided to use is hash table, the reason is hash table structure allows search and insert for elements in constant which is O(n) time complexity, and is crucial for handling data set of that larger, in this case is all the 252 integers. Therefore I have created a hash table type and a node element that will be stored in each bucket of the hash table where each node stores the integer and its colouring.
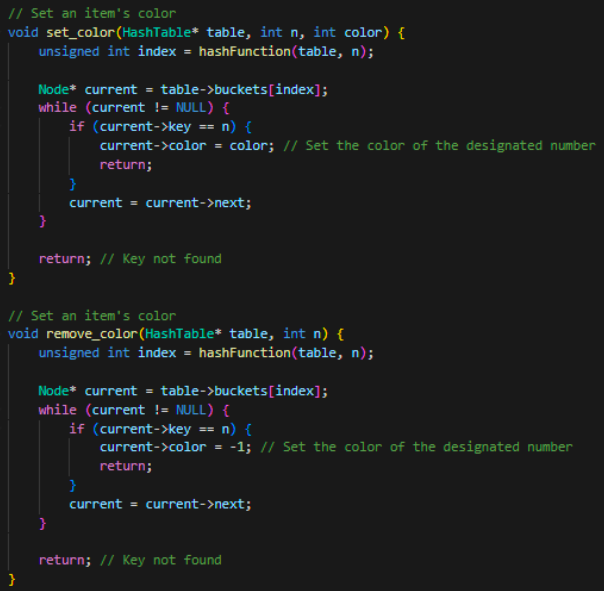
Then, corresponding members functions and helper function is created to manipulate the hash table and functions related to the main loop. Which specifically are the hash function for determining the index, which in this project I chose a relatively easy function to compute for clarity which is the modulus of the hash table size. I have also wrote a set and remove colour for future manipulation on the number's colour. And most importantly the check for monochromatic algorithm.
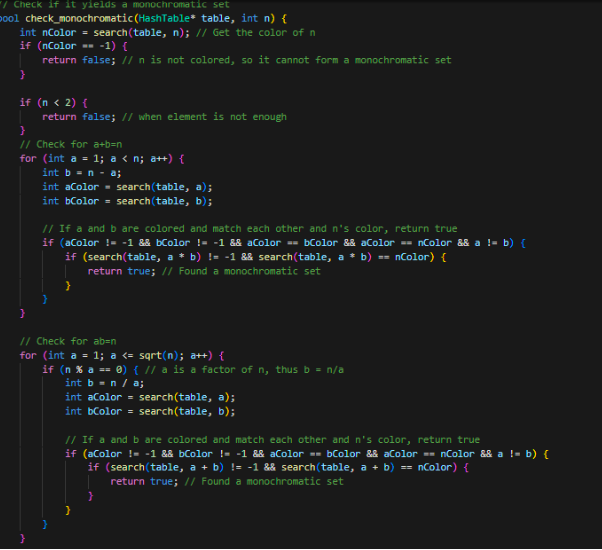
The monochromatic check function utilizes the fact that in the back tracing algorithm I implemented, it assumes the most significant integer to be of a+b or ab, therefore search algorithm breaks down the current integer in the iteration and checks if the number can be of these two cases. The case for a+b is quite easy where setting a variable a and let a iterate through 1 to n2, and from subtraction of n and a we are able to obtain b.
However in ab case, a needs to take value from 1 to √n which initially did not come straight into my mind.
After finding the corresponding factors, the program will check the node's number which is set when inserted. However in ab case, a needs to take value from 1 to the node?s number which is set when inserted.
The main function which is where the main program runs, first initialize the first number inserted, which is 1, and a highest success which will be used to check for monochromatic in later iterations. Since the program will trace all the way back down to one, therefore the last iteration will make the current checked number be 0, thus the loop is set to end when the number is less than or equal to 1. As the loop goes, the hash table tracks how many elements are in the hash table and will print it out in the terminal when the program terminates.