Section 46.1 Problems: Ramsey's Theorem and Graphs
Problem 46.1.1.
Every graph on at least \({k+l\choose k}\) vertices contains either a complete graph with \(k+1\) vertices or an independent set of \(l+1\) vertices.
Let \(V(G)\) be the set of vertices of the graph \(G\text{.}\)
We will prove the claim by induction on \(k+l\text{.}\)
If \(k=l=1\text{,}\) then \({k+l \choose k}={2\choose 1}=2\text{.}\) Let \(G\) be a graph with two vertices \(a\) and \(b\text{.}\) If \(a\) and \(b\) are adjacent then there is a complete graph with \(k+1=1+1=2\) vertices. If they are not adjacent, then there are \(l+1=1+1=2\) independent vertices.
Suppose that \(n\geq 2\) is such that for any \(k,l\in \mathbb{N}\) such that if \(k+l=n\) and if \(|V(G)|\geq {{k+l} \choose k}\) then \(G\) contains either a complete graph with \(k+1\) vertices or an independent set of \(l+1\) vertices.
Let \(k,l\) be such that \(k+l=n+1\) and let \(G\) be a graph with \({k+l\choose k}\) vertices. Let \(x\in V(G)\) be a vertex, let \(u(x)\) be the number of vertices of \(G\) adjacent to \(x\) and let \(v(x)\) be the number of vertices in \(G\) not adjacent to \(x\text{.}\) Then
By the Pigeonhole Principle \(u(x) \geq {k+l-1\choose k-1}\) or \(v(x)\geq {k+l-1\choose k}\text{.}\)
Say that \(v(x)\geq {k+l-1\choose k}\text{.}\) Let \(G_v\) be the subgraph of \(G\) induced by the set of vertices not adjacent to the vertex \(x\text{.}\) Since \(k+(l-1)=n\text{,}\) by the induction hypothesis the graph \(G_v\) contains or a a complete graph with \(k+1\) vertices or an independent set of \(l\) vertices. If it contains a complete graph with \(k+1\) vertices, then the graph \(G\) also contains a complete graph with \(k+1\) vertices. If \(G_v\) contains a set \(A\) of \(l\) independent vertices, then the set \(A\cup\{ x\}\) is a set of \(l+1\) independent vertices in \(G\text{.}\)
Say that \(u(x)\geq {k+l-1\choose k-1}\text{.}\) Let \(G_u\) be the subgraph of \(G\) induced by the set of vertices adjacent to the vertex \(x\text{.}\) Since \((k-1)+l=n\text{,}\) by the induction hypothesis the graph \(G_u\) contains or a a complete graph with \(k\) vertices or an independent set of \(l+1\) vertices. If it contains a \(l+1\) independent vertices, then the graph \(G\) also contains a set with \(l+1\) independent vertices. If \(G_u\) contains a complete graph with \(k\) vertices, then since the vertex \(x\) is adjacent to each of those \(k\) vertices, a complete graph on $\(k+1\) vertices in \(G\) appears, which completes the proof.
Problem 46.1.2.
Let \(k \geq 2\) and let \(a_{i},\dots, a_{k}\) be given positive integers. Prove that there exists a natural number \(n=R_{k}(a_{1},\ldots,a_{k})\) such that, if we \(k\)–colour the edges of the complete graph \(K_{n}\text{,}\) there will be an \(1 \leq i \leq k\) and a complete \(K_{a_{i}}\)–graph all of whose edges are coloured with the \(i^{th}\) colour.
Proof by induction.
By Problem 46.1.1, \(R_2(a_1, a_2)\) exists and \(R_2(a_1, a_2)\leq {a_1+a_2-2\choose a_1-1}\text{.}\)
Suppose that \(k \geq 3\) is such that \(R_{k-1}(b_{1},\dots,b_{k-1})\) exists for any choice of \(b_1,\ldots,b_{k-1}\in \mathbb{N}\text{.}\) Let \(a_{i},\dots, a_{k}\) be positive integers. Then both \(\alpha=R_2(a_{k-1},a_k)\) and \(\beta= R_{k-1}(1_{1},\dots,a_{k-2},\alpha)= R_{k-1}(a_{1},\dots,a_{k-2},R_2(a_{k-1},a_k))\) exist.
Let \(E=E(K_\beta)\) be the set of edges of the complete graph \(K_\beta\) and let \(C:E\to\{c_1,\ldots,c_{k-2},c_{k-1},c_k\}\) be an edge \(k\)–colouring of \(K_\beta\text{.}\) We define a \((k-1)\)–colouring \(C^\prime:E\to\{c_1,\ldots,c_{k-2},c^\prime\}\) in the following way. For \(e\in E\text{:}\)
If \(C(e)=c_i\) for some \(i\in[1,k-2]\text{,}\) then \(C^\prime(e)=C(e)\text{.}\)
If \(C(e)=c_i\) for some \(i\in[k-1,k]\text{,}\) then \(C^\prime(e)=c^\prime\text{.}\)
Then, by definition of \(R_{k-1}(1_{1},\dots,a_{k-2},\alpha)\text{,}\) there is a \(c_i\)–monochromatic complete graph \(K_{a_i}\) for some \(i\in[1,k-2]\) or there is \(c^\prime\)–monochromatic complete graph \(K_{R_2(a_{k-1},a_k)}\text{.}\) But going back to colouring \(C\text{,}\) \(K_{R_2(a_{k-1},a_k)}\) is \(2\)–coloured by colours \(c_{k-1}\) and \(c_k\text{.}\) By definition of \(R_2(a_{k-1},a_k)\text{,}\) there must be a \(c_{k-1}\)–monochromatic \(K_{a_{k-1}}\) or a \(c_{k}\)–monochromatic \(K_{a_{k}}\text{.}\)
Therefore if, for \(k\geq 3\text{,}\) \(R_{k-1}(b_{1},\dots,b_{k-1})\) exists for any \(b_1,\ldots,b_{k-1}\in \mathbb{N}\) then \(R_{k}(a_{1},\dots,a_{k})\) exists for any \(a_1,\ldots,a_{k}\in \mathbb{N}\text{,}\) with \(R_{k}(a_{1},\dots,a_{k})\leq R_{k-1}(a_{1},\dots,a_{k-2},R_2(a_{k-1},a_k)) \text{.}\)
By the Principle of Mathematical Induction, this completes the proof.
Problem 46.1.3.
Prove that \(R_{k}(3) \stackrel{\text{def}}{=} R_{k}(3,\dots,3) \leq \lfloor e \cdot k!\rfloor + 1\) and that equality holds for \(k=2\) and \(k=3\text{.}\)
We first prove \(R_k(3)\leq 2+k(R_{k-1}(3)-1)\text{,}\) then we use this fact to establish the upper bound for \(R_k(3)\leq \lfloor e\cdot k!\rfloor+1\text{.}\)
Let \(N=2+k(R_{k-1}(3)-1)\text{.}\) We consider the complete graph \(K_N\) and a \(k\)–colouring \(C:E(K_N)\to \{c_2,c_2,\ldots,c_k\}\) of its edges. We fix a vertex \(v\) and observe that \(v\) is incident to \(N-1=k(R_{k-1}(3)-1)+1\) edges. Each of those edges is coloured by one of \(k\) colours \(c_2,c_2,\ldots,c_k\text{.}\) By the Pigeonhole Principle, there is \(i\in[1,k]\) and a set \(S\subset E(K_N)\) of size \(R_{k-1}(3)\) such that all edges connecting the vertex \(v\) and a vertex in \(S\) have the colour \(c_i\text{.}\) If any two vertices in \(S\) are connected by an edge of the colour \(c_i\text{,}\) then there is a monochromatic triangle in colour \(c_i\text{.}\) If not, the edges of the complete graph with the vertex set \(S\) is edge \((k-1)\)–coloured. Since \(|S|\geq R_{k-1}(3)\text{,}\) by definition of \(R_{k-1}(3)\text{,}\) the complete graph with the vertex set \(S\) has a monochromatic triangle in one of the remaining \(k-1\) colours.
Hence, \(R_k(3)\leq 2+k(R_{k-1}(3)-1)\text{.}\)
Now we can show by induction on \(k\) that \(R_k(3)\leq 1+k!(\sum_{i=0}^{k}1/i!)\leq 1+\lfloor{k!e}\rfloor\text{.}\)
Recall that \(R_2(3)=R(3,3)= 6\text{,}\) i.e., recall the dinner–party problem, which states that in a party of \(6\) people, either \(3\) of them mutually know each other, or \(3\) of them are mutually strangers. This together with \(1+2!(\sum_{i=0}^{2}1/i!)= 1+2(1+1+\frac{1}{2})=6\) and \(1+\lfloor{2!e}\rfloor=1+5=6\text{,}\) establishes the base case of induction.
Suppose that the claim is true for some \(k-1\geq 2\text{.}\)Then, since\(\lfloor{e\cdot k!}\rfloor=k\lfloor{e(k-1)!}\rfloor+1\text{,}\) it follows that
which establishes the induction step.
We have shown that \(R_3(3)\leq 1+\lfloor{3!e}\rfloor=1+16=17\text{.}\) Next, we \(3\)–colour the edges of the complete graph \(K_{17}\) with red, green or blue and fix a vertex \(v\text{.}\) By the Pigeonhole Principle there is a set of vertices \(S\subset V(K_{17})\text{,}\) \(|S|\geq 6\text{,}\) such that all edges between \(v\) and a vertex that belongs to \(S\) are of the same colour, say red. If any two vertices in \(S\) are connected by a red edge, then there is a red triangle. If not, the complete graph with the vertex set \(S\) is edge \(2\)–coloured. Since \(|S|\geq R_{2}(3)=6\text{,}\) the complete graph with the vertex set \(S\) has a green or a blue triangle. Hence, \(R_3(3)\geq 17\text{,}\) which completes the proof.
Problem 46.1.4.
Prove that for \(k \geq 2\text{,}\) \(2^{k/2} \leq R_{2}(k,k) \lt 2^{2k}.\)
By Problem 46.1.1, for \(k\geq 2\text{,}\) \(R_{2}(k,k)\leq {2k-2\choose k-1}\text{.}\) Since
it follows that \({2(k-1)\choose k-1}=\frac{(2(k-1))!}{((k-1)!)^2}\lt 2^{2(k-1)}\text{,}\) which establishes the upper bound.
Now we prove \(R(k,k)\gt 2^{k/2}\text{.}\) Let \(\Omega\) be the set of all graphs on the set of vertices \(V=\{v_1,\cdots,v_n\}\text{.}\) There are \(2^{n\choose 2}\) such graphs. Let \(P:\Omega \to [0,1]\) be the uniform probability distribution, so every graph on \(V\) is equally likely, that is for all \(i\neq j\text{,}\)
Let \(S_1,\ldots,S_{n\choose k}\) be an enumeration of all different \(k\)–subsets of \(V\text{.}\) For \(i=1,\ldots,{n\choose k}\text{,}\) let \(E_i\) be the event that \(S_i\) forms either a \(k\)–complete graph or a \(k\)–independent set in the graph. Then \(P(E_i)=2\cdot 2^{-{k\choose 2}}=2^{-{k\choose 2}+1}\)
Let \(E= \bigcup_{i=1}^{n\choose k}E_i\text{,}\) i.e., let \(E\) be the event that a random graph on the set of vertices \(V\) contains a \(k\)–complete graph or a \(k\)–independent set. Then
Since, for \(k\geq 2\text{,}\) \({n\choose k}\leq \frac{n^k}{2^{k-1}}\text{,}\) if \(n\leq 2^{k/2}\text{,}\) it follows
For \(k\geq 4\text{,}\) \(2^{2-(k/2)}\lt 1\text{,}\) or \(P(E)\lt 1\) thus \(P(\Omega\backslash E)=1-P(E)\gt 0\text{.}\) Note that \(P(\Omega\backslash E)\) is the probability that in a random graph of size \(n\leq 2^{k/2}\text{,}\) with no \(k\)–complete graph or \(k\)–independent set. Since \(P(\Omega\backslash E)\gt 0\text{,}\) such graph must exist for any \(n\leq 2^{k/2}\text{.}\) Thus, \(R(k,k)\gt 2^{k/2}\text{.}\)
Problem 46.1.5.
Prove that in any edge \(2\)–colouring of the complete graph \(K_n\) , \(n\geq 3\text{,}\) there will be a Hamiltonian circuit which either is monochromatic or consists of two monochromatic arcs.
Remark 46.1.6.
A Hamilton circuit in a graph is a circuit that passes through each vertex of a graph exactly once. Not all graphs have a Hamilton circuit, but complete graphs do have Hamilton circuits.
Proof by induction.
For the base case \(n=3\text{,}\) there must be two adjacent edges coloured by the same colour. If the third edge is of the same colour, there is a monochromatic Hamiltonian circuit. Otherwise, there are two monochromatic arcs.
Suppose that \(n\gt 4\) is such that n any \(2\)–colouring of the complete graph \(K_{n-1}\) there will be a Hamiltonian circuit which either is monochromatic or consists of two monochromatic arcs.
Let \(c\) be an edge \(2\)–colouring of \(K_n\text{,}\) say in blue and red. Let \(X\) be a vertex and let \(K_{n-1}\) be the complete graph induced by the set of vertices \(V(K_n)\backslash\{X\}\text{.}\) Let \(c^\prime\) be restriction of \(c\) on \(E(K_{n-1})\text{.}\) By the induction hypothesis, there is a Hamiltonian circuit \(C^\prime\) in \(K_{n-1}\text{,}\) which is either monochromatic or has two vertices \(A\) and \(B\) such that one \((AB)\)–arc \(P\) is red, while the other one, \(Q\) is blue. The monochromatic case can be regarded as the case when \(A=B\) and the arc \(Q\) consists only of the vertex \(A\text{.}\)
Assume that edge \(AX\) is red. Let \(U\) be the vertex that lies on the arc \(Q\) next to the vertex \(A\) (if \(Q\) consists of a single point, \(U\) can be any neighbour of \(A\) on the path \(P\)). Then \(P + AX +XU + Q\backslash\{ (AU)\}\) is a Hamiltonian circuit in \(K_n\)such that either the two \((BX)\)–arcs are red and blue or the two \(BU\) arcs are so.
Refer to the graphs below for a visual illustration of the inductive step with \(k=6\) as an example.
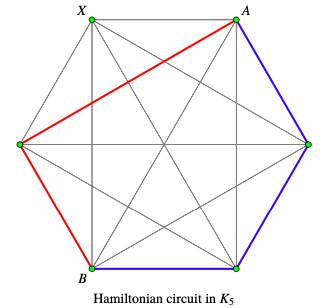
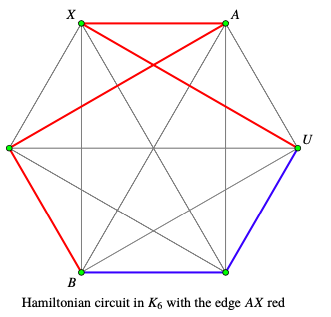
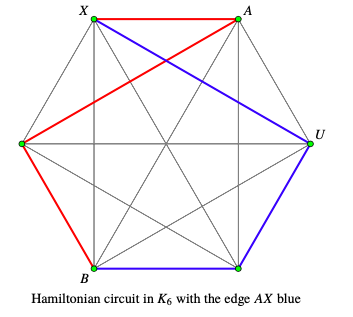
Problem 46.1.7.
Prove that in any edge \(2\)–colouring of the complete graph \(K_{\lfloor \frac{3k+1}{2} \rfloor}\) , \(k\geq 1\text{,}\) there will be a monochromatic path of length \(k\text{.}\)
Proof by induction.
If \(k=1\text{,}\) then we edge colour the complete graph \(K_2\text{,}\) so there must a monochromatic path of length \(k=1\text{.}\)
If \(k=2\text{,}\) then we edge colour the complete graph \(K_3\text{.}\) Since by the Pigeonhole Principle, we need to use one of the colours at least twice, there will be a monochromatic path of length \(k=2\text{.}\)
If \(k=3\text{,}\) then we edge colour, say red and blue, the complete graph \(K_5\text{.}\) Denote the vertices of \(K_5\) by \(A,B,C,D,E\text{,}\) oriented counterclockwise. By the Pigeonhole Principle, the vertex \(A\) is incident with at least two edges of the same colour. Say that \(AB\) and \(AC\) are red. If one of the edges \(BD, BE, CD, CE\) is red, there is red path \(\color{red}{C-A-B-X}\) or \(\color{red}{B-A-C-X}\text{,}\) with \(X\in\{D,E\}\text{,}\) of length \(k=3\text{.}\) If all \(BD, BE, CD, CE\) are blue then there is a blue path \(\color{blue}{E-B-D-C}\) of length \(k=3\text{.}\)
If \(k=4\text{,}\) then we edge colour, say red and blue, the complete graph \(K_6\text{.}\) Denote the vertices of \(K_6\) by \(A,B,C,D,E,F\text{,}\) oriented counterclockwise. Since \(K_6\) contains a complete graph \(K_5\) as a subgraph, there must a monochromatic path of length \(3\text{.}\) Say that the path \(\color{red}{A-B-C-D}\) is red. If any of the edges \(AE, AF, DE, DF\) is red, there is a red path \(\color{red}{X-A-B-C-D}\) or \(\color{red}{A-B-C-D-X}\text{,}\) with \(X\in\{E,F\}\text{,}\) of length \(k=4\text{.}\)
Suppose that all \(AE, AF, DE, DF\) are blue. If any of the edges \(BE, BF, CE, CF\) is blue, there is a blue path \(\color{blue}{A-F-D-E-X}\) or \(\color{blue}{D-E-A-F-X}\text{,}\) with \(X\in \{B,C\}\text{,}\) of length \(k=4\text{.}\) If all of the edges \(BE, BF, CE, CF\) are red then \(\color{red}{A-B-F-C-D}\) is a red path of length \(k=4\text{.}\)
The statement is true for \(k\in\{1,2,3,4\}\text{.}\)
As the induction step, suppose that \(k\geq 5\) is such that the statement is true for \(k-1\text{,}\) i.e., suppose that \(k\) is with the property that any edge \(2\)–colouring of the complete graph \(K_{\lfloor \frac{3k+1}{2} \rfloor}\) contains a monochromatic path of length \(k-1\text{.}\)
Let \(c\) be a blue and red edge colouring of \(G=K_{\lfloor \frac{3k+1}{2} \rfloor}\text{.}\) Let \({\color{red}{\cal{P}}=P_1-P_2-\cdots -P_k}\) be a \(c\)-monochromatic, say red, path in \(G\) of length \(k-1\) guaranteed by the inductive hypothesis.
Since \(\lfloor \frac{3k+1}{2} \rfloor -k \gt \frac{3k-1}{2}-k=\frac{k-1}{2}\geq 2\text{,}\) it follows that there are at least three vertices that do not belong to the path \(\color{red}{\cal{P}}\text{,}\) say \(V(G)\backslash V(\color{red}{\cal{P}})=\{V_1,V_2,\ldots,V_m\}\text{,}\) \(m\geq 3\text{.}\)
If any of the edges \(P_1V_j\) or \(P_kV_j\text{,}\) for any \(1\leq j\leq m\) is red, then there is a red path \(\color{red}{V_j - P_1-\cdots-P_k}\) or \(\color{red}{P_1-\cdots-P_k-V_j}\) of length \(k\text{.}\) If there are \(1\leq j\leq m\) and \(2\leq i\leq k-2\) such that both \(P_iV_j\) and \(P_{i+1}V_j\) are red, then the red path \(\color{red}{P_1 - \cdots - P_i -V_j - P_{i+1} - \cdots - P_k}\) is of length \(k\text{.}\)
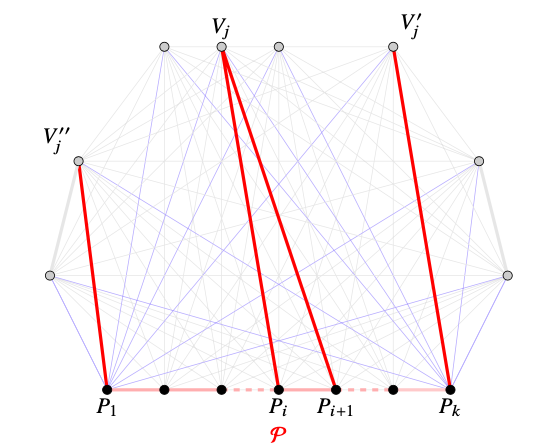
We assume that the colouring \(c\) is such that for each \(1\leq j\leq m\) all \(P_1V_j\) and \(P_kV_j\) are blue and that for each \(2\leq i\leq k-2\) at least one of the edges \(P_iV_j\) and \(P_{i+1}V_j\) is blue.
As the image depicts, in the case \(k=5\text{,}\) any colouring \(c\) satisfying the above constraints contains a blue path \(\color{blue}{P_3-V_1-P_1-V_3-P_5-V_2}\) of length \(k=5\text{.}\)
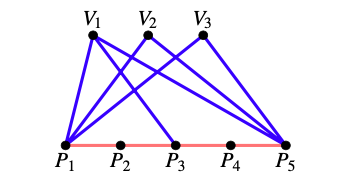
Let the family \({\cal{F}}=\{({\cal{Q}}_1, {\cal{Q}}_2): {\cal{Q}}_1, {\cal{Q}}_2\subset V(G)\backslash V(\color{red}{\cal{P}})\}\) be such that:
\({\cal{Q}}_1\) and \({\cal{Q}}_2\) are two nonempty disjoint sets.
If \(i\in\{1,2\}\) is such that \(|\cal{Q}_i|=q_i\gt 1\) then there is a set \(\cal{P}_i\subset{\cal{P}}\backslash\{P_1,P_k\}\text{,}\) \(|\cal{P}_i|=q_i-1\) and enumerations \({\cal{Q}}_i=\{Q_{j_1}, Q_{j_2},\ldots, Q_{j_2}\}\) and \({\cal{P}}_i=\{P_{j_1},P_{j_2},\ldots,P_{j_{q_i-1}}\}\) such that the path \(Q_{j_1} - P_{j_1} - Q_{j_2} - \cdots - P_{j_{q_i-1}} - Q_{j_{q_i}}\) is blue. If \(q_1\gt 1\) and \(q_2\gt 1\) then \(\cal{P}_1\) and \(\cal{P}_2\) are disjoint sets. In the case that \(i\in\{1,2\}\) is such that \(|\cal{Q}_i|=q_i= 1\text{,}\) we take \(\cal{P}_i=\emptyset\text{.}\)
The family \({\cal{F}}\) is nonempty because, for any \(V^\prime,V^{\prime\prime}\in V(G)\backslash V(\color{red}{\cal{P}})\text{,}\) \((\{V^\prime\},\{V^{\prime\prime}\})\in {\cal{F}}\text{.}\)
Let, for the given colouring \(c\text{,}\) sets \((\cal{Q}_1,\cal{Q}_2)\in \cal{F}\) be such that \(|\cal{Q}_1\cup \cal{Q}_2|\geq 2\) is the largest possible. We claim that in that case \({\cal{Q}_1}\cup {\cal{Q}_2}=V(G)\backslash V(\color{red}{\cal{P}})\text{.}\)
Suppose that this is not true, i.e., suppose that \(|\cal{Q}_1\cup \cal{Q}_2|\) is the largest possible but that there is \(X\in V(G)\backslash V(\color{red}{\cal{P}})\) that does not belong to \({\cal{Q}_1}\cup {\cal{Q}_2}\text{.}\)
From \(|\{P_2,P_3,\ldots,P_{k-1}\}\backslash ({\cal{P}_1}\cup{\cal{P}_2})|=k-2-(q_1-1)-(q_2-1)=k -(q_1+q_2)\) and \(q_1+q_2\lt |V(G)\backslash V(\color{red}{\cal{P}}))| =\lfloor \frac{3k+2}{2}\rfloor -k \) it follows that
Hence at least \(\lfloor \frac{k}{2}\rfloor+1\) vertices among \(k-1\) vertices in \(\{P_2,P_3,\ldots,P_{k-1}\}\) do not belong to \({\cal{P}_1}\cup{\cal{P}_2}\text{.}\) By the Pigeonhole Principle, there is \(\ell\in\{2,\ldots,k-2\}\) such that neither of \(P_\ell\) and \(P_{\ell+1}\) belongs to \({\cal{P}_1}\cup{\cal{P}_2}\text{.}\)
For \(i\in\{0,1\}\text{,}\) if \(q_i=1\) denote by \(Q_i\) the unique elemnt of \({\cal{Q}}_i\text{,}\) or if \(q_i\gt 1\) denote by \(Q_i\) one of the end vertices of the path determined by \({\cal{Q}}_i\text{.}\)
By our assumption about the colouring \(c\) at least one of the edges \(XP_{\ell -1}\) or \(XP_{\ell}\) is blue. Say, \(XP_{\ell -1}\) is blue. Otherwise, for example, \(|({\cal{Q}}_1\cup\{X\})\cup{{\cal{Q}}_2}|>q_1+q_2\text{.}\)
But then, our assumption about the colouring \(c\) implies that both \(Q_1P_{\ell }\) or \(Q_2P_{\ell}\) are blue and consequently \(({\cal{Q}}_1\cup{\cal{Q}}_2,\{X\})\in {\cal{F}}\text{.}\)
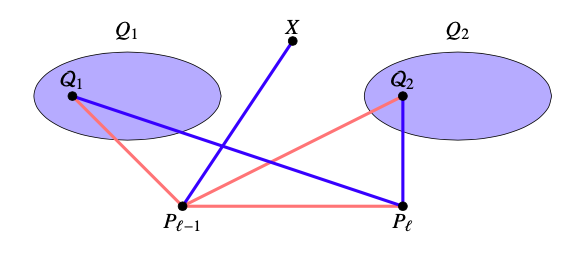
This again contradicts the maximality of \(|\cal{Q}_1\cup \cal{Q}_2|\text{.}\) Hence \({\cal{Q}}_1\cup {\cal{Q}}_2=V(G)\backslash V(\color{red}{\cal{P}})\text{.}\)
If \(i\in\{1,2\}\) is such that \(|{\cal{Q}}_i|\gt 1\) let \(Q_i^\prime\) be the other end vertex of the path determined by \({\cal{Q}}_i\text{.}\) Otherwise, \(Q_i^\prime=Q_i\text{.}\) The length of blue circuit
is
If \(k\) is an odd number, then \(L(\color{blue}{{\cal{B}}})=2\left(\frac{3k+1}{2} -k\right)=k+1\) and therefore there is a blue path of length \(k\text{.}\)
If \(k\) is an even number, then \(L(\color{blue}{{\cal{B}}})=2\left(\frac{3k}{2} -k\right)=k\text{.}\) Since, as previously established, \(|\{P_2,P_3,\ldots,P_{k-1}\}\backslash ({\cal{P}}_1\cup{\cal{P}}_2)|\gt \frac{k}{2}\text{,}\) there is \(j\in\{2,\ldots,k-2\}\) such that neither of \(P_j\) nor \(P_{j+1}\) belongs to \({\cal{P}}_1\cup{\cal{P}}_2\text{.}\) Our assumption about the colouring \(c\) implies that at least one the edges \(Q_1P_j\) and \(Q_1P_{j+1}\) is blue. Say that \(Q_1P_j\) is blue and denote by \(R\) the vertex on the circuit \(\color{blue}{{\cal{B}}}\) that is adjacent to \(Q_1\) and it is not \(P_1\text{.}\) But then the path \(P_j - Q_1 - Q_2^\prime - \cdots - R\) is of length \(k\text{,}\) which completes the proof.
Problem 46.1.8.
Let us \(2\)–colour the edges of \(K_n\text{,}\) a complete \(n\)–graph. Prove the following assertions:
If there is a monochromatic \((2k+1)\)–circuit, \(k \geq 3\text{,}\) then there is a monochromatic \(2k\)–circuit.
If there is a monochromatic \(2k\)–circuit, \(k \geq 3\text{,}\) then there is either a monochromatic \((2k-1)\)–circuit or two monochromatic disjoint complete \(k\)–graphs.
-
If \(n \geq 2m-1\) and \(n \geq 6\text{,}\) then there will be a monochromatic \(m\)–circuit.
Note 46.1.9.
Use the fact that if a graph \(G\) is such that \(|V(G)|=2\alpha(G)+1\) and, for every \(x,y \in V(G)\text{,}\) \(\alpha(G-x-y)=\alpha(G)\) then \(G\) is an odd circuit. (This is Problem 8.26 in Lovasz's book. As it is common, \(\alpha(G)\) denotes the size of the largest independent set of \(G\text{.}\))
For \(m\geq 2\text{,}\) by \(C_m\) we denote a circuit of length \(m\text{.}\)
-
Let \(\left(v_0,\dots,v_{2k}\right)\) be cyclic ordering of the vertices of our red monochromatic cycle of length \(2k+1\text{.}\) We need show that there is a monochromatic cycle of length \(2k\)
If any edge of the form \((v_i,v_{i+2})\text{,}\) where the indices are taken modulo \(2k+1\) is red, we then form a red cycle \(C_{2k}\) by using all vertices except \(v_{i+1}\text{.}\) Hence we assume that all edges \((v_i,v_{i+2})\) are blue.
We now have the circuit \((v_0,v_2,\dots,v_{2k},v_1,v_3,\dots,v_{2k-1})\text{,}\) and these blue edges form a blue \(C_{2k+1}\text{,}\) since 2 and \(2k+1\) are co–prime. If any edge of the form \((v_i,v_{i+4})\) is blue, we obtain a blue \(C_{2k}\) by using all vertices except \(v_{i+2}\text{.}\) Thus, we assume that all such edges are red.
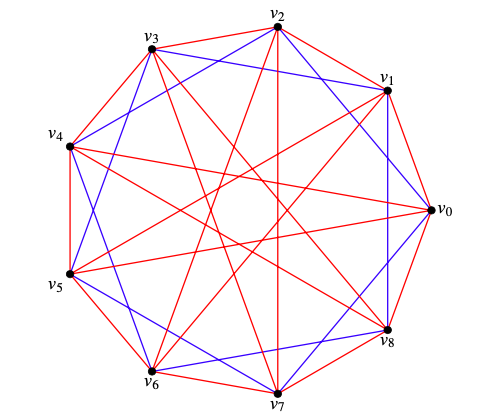
Consequently they form another red \(C_{2k+1}\text{.}\)
If \(k=2\text{,}\) the two \(C_{2k+1}\) are the same, and \(-1\equiv 4\pmod 5\text{,}\) so assume \(k\geq 3\text{.}\) If the edge \((v_0,v_3)\) is red, then \((v_0,v_3,v_2,v_1,v_5,v_6,v_7,\dots,v_{2k})\) forms a red \(C_{2k}\text{,}\) using all vertices but \(v_4\text{.}\) By symmetry, any edge of the form \((v_i,v_{i+3})\) is blue, then \((v_0,v_3,v_6,v_8,v_{10},\dots,v_{2k},v_1,v_{2k-1},v_{2k-3},\dots,v_9,v_7,v_5,v_2)\) forms a blue \(C_{2k}\) using all vertices but \(v_4\text{.}\)
-
Let \((v_0,\dots,v_{2k-1})\) be a red \(C_{2k}\text{.}\)
Suppose there is no monochromatic \(C_{2k-1}\text{.}\) Similar to the first part of this problem, if \((v_i,v_{i+2})\) is red, then we trivially have a red \(C_{2k-1}\text{,}\) so our assumption implies that \((v_i,v_{i+2})\) is blue for \(1\leq i\leq 2k\text{.}\)
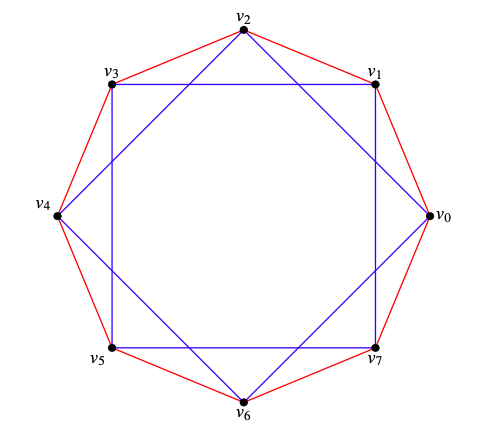
We claim that \((v_i,v_{i+2\nu})\) is blue for \(1\leq i\leq 2k\) and \(1\leq \nu\leq k-1\text{,}\) i.e that two \(k\)–complete graphs induced by sets \(\{v_0,v_2,\ldots,v_{2k-2}\}\) and \(\{v_1,v_3,\ldots,v_{2k-1}\}\) are blue.
Say that, for example, \((v_0,v_{2\nu})\) is red.
To avoid the \((2k-1)\)–circuit \((v_0,v_{2\nu},v_{2\nu -1},\cdots,v_1,v_{2\nu +2}, \cdots,v_{2k-1})\) to be red, the edge \((v_1,v_{2\nu +2})\) must be blue.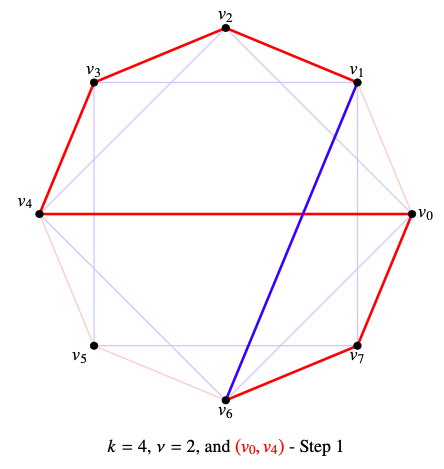
To avoid the \((2k-1)\)–circuit \((v_0,v_1,\dots,v_{2\nu -2},v_{2k-1},v_{2k-2},\dots,v_{2\nu})\) to be red, the edge \((v_{2\nu -2},v_{2k-1})\) must blue.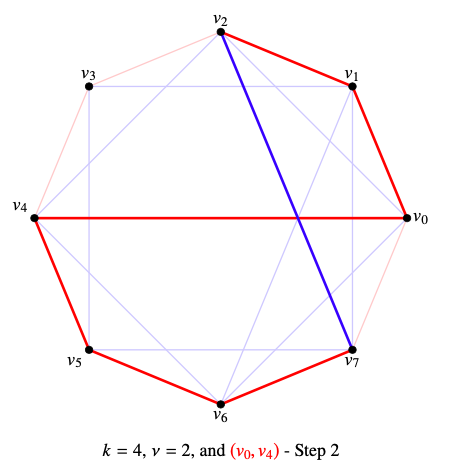
But now the \((2k-1)\)– circuit\begin{equation*} (v_{2k-1},v_{2\nu -2},v_{2\nu -4},\dots,v_0,v_{2k-2},\dots, \end{equation*}\begin{equation*} v_{2\nu +2},v_1,v_3,\dots,v_{2k-3}) \end{equation*}is blue.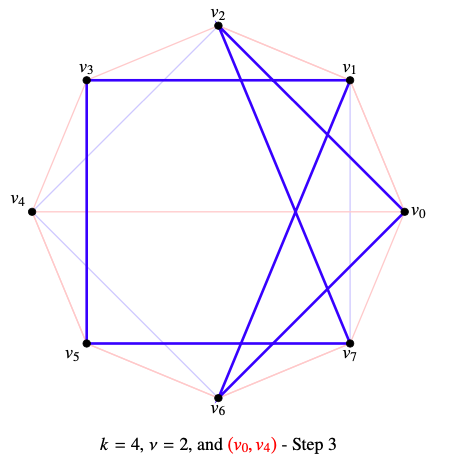
This contradiction means that \((v_0,v_{2\nu})\) must be blue. Thus, \((v_i,v_{i+2\nu})\) is blue for all \(1\leq i\leq 2k\) and all \(1\leq \nu\leq k-1\text{,}\) which completes the proof.
-
Let \(m\geq 4\text{,}\) let \(n\geq 2m-1\text{,}\) and let \(c\) be a red-blue edge colouring of the complete graph \(G=K_n\text{.}\)
If \(m=4\) then \(n\geq 7\text{.}\) Since \(n\geq R(3,3)=6\text{,}\) there is a \(c\)–monochromatic, say red, triangle \((v_1,v_2,v_3)\text{.}\) If there is \(v\in V(G)\backslash\{v_1,v_2,v_3\}\) such that at least two of the three edges \((v,v_1)\text{,}\) \((v,v_2)\text{,}\) and \((v,v_3)\) are red, then there is a red path, say, \((v,v_1,v_3,v_2)\) of length \(4\text{.}\) If there is no such \(v\text{,}\) we think about sets \(\{v_1,v_2\},\{v_1,v_3\}\text{,}\) and \(\{v_2,v_3\}\) as pigeonholes. We put the vertex \(v\in V(G)\backslash\{v_1,v_2,v_3\}\) into the pigeonhole \(\{v_i,v_j\}\) if both \((v,v_i)\) and \((v,v_j)\) are blue. In the case that all three \((v,v_1)\text{,}\) \((v,v_2)\text{,}\) and \((v,v_3)\) are blue, we choose the pigeonhole \(\{v_1,v_2\}\text{.}\) By the Pigeonhole Principle there are \(u,v\in V(G)\) \((v,v_1)\) such that \(u\) and \(v\) belong to the same pigeonhole, say, \(\{v_i, v_j\}\text{.}\) But then there is a blue path, say, \((v,v_i,v,v_j)\text{.}\)
Let \(m\geq 5\) and suppose the colouring \(c\) uses both colours. Then there are two graphs \(G_R\) and \(G_B\) that are formed by red and blue edges respectively. Since \({|E(G_R)|+E|(G_B)|}= {{n}\choose {2}}\text{,}\) by the Pigeonhole Principle, for at least one of them, say for \(G_R\text{,}\)
\begin{equation*} |E(G_R)|\geq \frac{1}{2}{{n}\choose 2}\geq\frac{m-1}{2}\cdot n>\frac{(m-1)(|V(G_R)|-1)}{2}\mbox{.} \end{equation*}By Note 46.1.9, \(G_R\) has an \(s\)–circuit for some \(s\geq m\text{,}\) i.e., the complete graph \(K_n\) contains a monochromatic circuit of the size of least \(m\text{.}\)
Let \(C\) be a monochromatic \(s\)–circuit, for the smallest possible \(s\geq m\text{.}\)
By the first two parts of this Problem, there is a monochromatic \((s-1)\)–circuit, which contradicts our choice of \(s\text{,}\) or \(s=2k\) is even and we have two disjoint complete graphs, say \(J\text{,}\) \(K\text{,}\) that are both coloured blue, if we assume that \(C\) is red. Since \(V(C)\subseteq V(J)\cup V(K)\) and \(\min\{|V(J)|,|V(K)|\}\geq k\text{,}\) we choose \(J\) and \(K\) for which \(|V(J)|+|V(K)|\geq 2k\) is maximal.
If \(|V(J)|+|V(K)|= |V(G)|\geq 2m-1\text{,}\) then by the Pigeonhole Principle, at least one of the blue coloured complete graphs \(J\text{,}\) \(K\) contains as a subgraph a complete graph on at least \(m\) vertices. Hence, in this case there is a blue circuit of length \(m\text{.}\)
Suppose that \(2k\leq |V(J)|+|V(K)|\lt |V(G)|\text{.}\)
We need to prove that \(2k=m\text{.}\)
Suppose \(2k\gt m\text{.}\)
If there are at least two independent blue edges that connect \(J\) to \(K\text{,}\) we have a blue \((2k-1)\)–circuit, contradicting our choice of \(s=2k\text{.}\) So, all blue edges, sitting in between \(J\) and \(K\) have a vertex \(x\in V(J)\) in common.
If \(m\) is even, then for \(S=V(J)\backslash\{x\}=\{u_1,u_2,\ldots,u_p\}\text{,}\) \(p\geq k-1\geq \frac{m}{2}\) and \(V(K)=\{w_1,w_2,\ldots,w_q\}\text{,}\) \(q\geq k\gt \frac{m}{2}\text{,}\) the circuit \((u_1,w_1,u_2,\ldots, u_\frac{m}{2}, w_\frac{m}{2})\) is red and of length \(m\text{,}\) which contradicts our assumption that \(s=2k>m\) is the length of the shortest monochromatic circuit of the length at least \(m\) .
Hence, suppose that \(m\) is odd.
Let \(v\in V(G)\backslash (V(J)\cup V(K))\text{.}\)
Suppose that \(v\) is joined by red edges to \(u\in S=V(J)\backslash\{x\}\) and \(w\in V(K)\text{.}\) Let \(S=\{u=u_1,u_2,\ldots,u_p\}\text{,}\) \(p\geq k-1\geq \frac{m-1}{2}\) and \(V(K)=\{w_1,w_2,\ldots,w_q\}\text{,}\) \(q\geq k\gt \frac{m-1}{2}\text{,}\) with \(w=w_{\frac{m-1}{2}}\text{.}\) The circuit \((v,u=u_1,w_1,u_2,\ldots, u_\frac{m-1}{2}, w_\frac{m-1}{2}=w)\) is red and of length \(m\text{,}\) which contradicts our assumption that \(s\gt m\) is the length of the minimal monochromatic circuit.
Observe that edges \((v,w)\text{,}\) \(w\in V(K)\text{,}\) cannot be all blue because the complete graph \(K^\prime\) with \(V(K^\prime) =V(K)\cup \{v\}\) would be blue with \(|V(J)|+|V(K^\prime)|\gt |V(J)|+|V(K)|\text{,}\) contradicting our choice of \(J\) and \(K\text{.}\)
Therefore, we may assume that all edges \((v,u)\text{,}\) \(u\in S= V(J)\backslash\{x\}\text{,}\) are blue.
Our assumption that there is no monochromatic circuit of length \(m\text{,}\) implies that \(|V(K)|\leq m-1\text{.}\)
Consider the set \(T=V(G)\backslash(S\cup V(K))\text{,}\) where \(S\) is as above. Then \(|S|+|T|\geq (2m-1)-(m-1)=m\text{,}\) with \(m-2\geq |S|\geq \frac{m-1}{2}\text{.}\) Since \(S\subset V(J)\text{,}\) all edges spanned by \(S\) are blue. Since \(x\not\in S\text{,}\) all edges joining \(S\) to \(T\) are blue.
If \(|S|>\frac{m-1}{2}\text{,}\) let \(S=\{u_1,u_2,\ldots, u_p\}\text{,}\) \(\frac{m+1}{2}\leq p\leq m-2\text{,}\) and \(T=\{v_1,v_2,\ldots,v_{t},\ldots, v_q\}\text{,}\) where \(t=m-p\lt m-\frac{m-1}{2}=\frac{m+1}{2}\leq p\text{.}\) Then the blue circuit \((u_1,v_1,u_2,\ldots u_t,v_t, u_{t+1},u_{t+2},\ldots, u_p)\) is of length \(t+p=m\text{.}\)
We may assume that \(|S|=\frac{m-1}{2}\text{.}\)
If there are \(v,v^\prime \in T\) such that the edge \((v,v^\prime)\) is blue, then for \(S=\{u_1,u_2, \cdots ,u_{\frac{m-1}{2}}\}\) and \(T=\{v=v_1,v_2,\ldots,v_q\}\text{,}\) where \(q\geq\frac{m+1}{2}\) and \(v'=v_{\frac{m+1}{2}}\text{,}\) the blue circuit \((v,u_1,v_2,u_2\ldots,u_{\frac{m-1}{2}},v^\prime)\) is of length \(m\text{.}\)
Hence, we may assume that \(T\) induces a complete red graph on at least \(\frac{m+1}{2}\) vertices and that \(\frac{m-1}{2}\leq |V(K)| =\ell \leq m-1\text{.}\)
Suppose that there are at least two independent red edges that connect \(T\) to \(K\text{,}\) say that there are \(v,v'\in T\) and \(w,w'\in V(K)\) such that the edges \((v,w)\) and \((v^\prime,w^\prime)\) are red. Let \(V(K)=\{w=w_1,w_2,\ldots,w_{\ell}\}\text{,}\) with \(w^\prime =w_{\frac{m-1}{2}}\text{,}\) and \(S=\{u_1,u_2,\ldots,u_{\frac{m-1}{2}}\}\text{.}\) Then, since \(x\not\in S\text{,}\) we have a red \(m\)–circuit \((v,w_1,u_1,w_2\ldots,u_{\frac{m-1}{2}-1},w^\prime,v^\prime)\text{.}\)
So, we consider the case that all red edges, sitting in between \(T\) and \(K\) have a vertex \(y\in V(K)\) in common. Since \(x\in T\) the edge \((x,y)\) is red and therefore belongs to the red circuit \(s\)–circuit \(C\text{.}\)
Let \(v\in T\backslash\{x\}\text{,}\) \(S=\{u_1,u_2,\ldots,u_{\frac{m-1}{2}}\}\text{,}\) and let \(V(K)\backslash \{y\}=\{w_1,w_2,\ldots,w_{\ell -1}\}\text{.}\) Then the blue circuit \((x,u_1,\ldots,u_{\frac{m-1}{2}},v,w_1,\ldots,w_{\frac{m-1}{1}-1\) is of the length \(m\text{.}\)
Therefore, \(s=m\text{,}\) which completes the proof.
