Section 15.1 Small Number and the Old Game
Written by: Veselin Jungic
Illustrated by: Listiarini Listiarini
Small Number is a young boy who gets into a lot of mischief. Today he is visiting his Auntie.

Auntie (lovingly): “You have grown so much since I saw you last time, Small Number. Tell me everything, how are you? How's school?”
Small Number (enthusiastically): “I am great! There is a new game that I really like to play on my phone. I am much better at it than any of my friends. School is going fine, except math. I know that you and my mom like math, but for me math is so boring.”


Auntie (understandingly): “I am sorry to hear that Small Number. And you are right, everyone in our family is good at math. But enough about that.”
Auntie (after a short pause): “It is good that you like to play games. That makes you think fast. Would you like me to show you a game that the ancestors of our Haida cousins used to play a long time ago?”
Small Number (surprised): “What? Our ancestors played games? But they didn't have computers and cellphones!”
Auntie (laughing): “You are funny, Small Number! Our ancestors liked to have fun in the same way you like to have fun with your friends.”

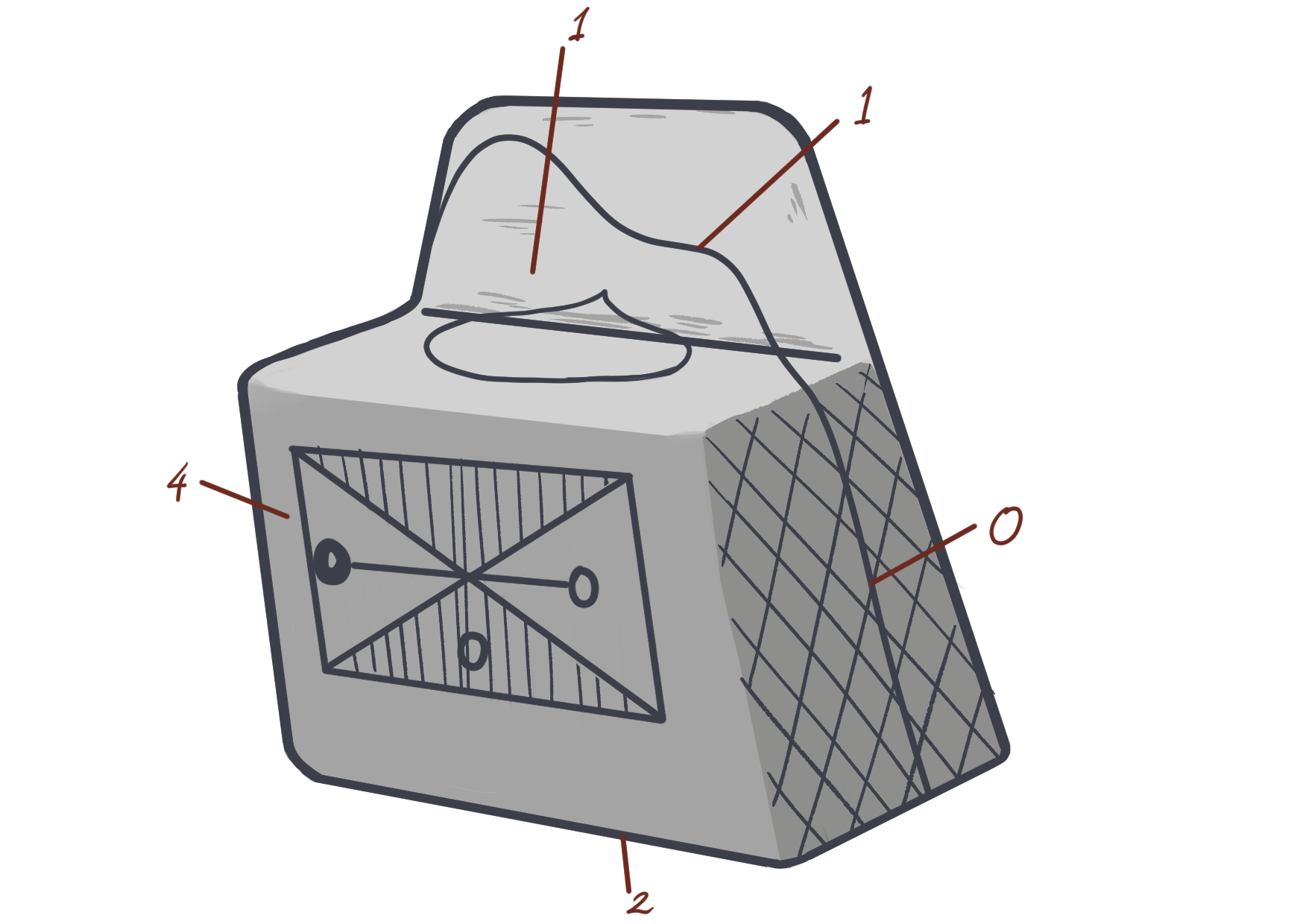
Auntie (thoughtfully, reaching for her tablet): “The game I would like to show you was called the Throwing Game. It used a die made from a piece of wood, bone, or ivory, something like this:”
The die was about eight centimetres high, with a base measuring, about four centimetres by two and a half centimetres, and most of the upper half was cut away, leaving a thin flange, extending upward on one side. A player would hold the die by the thin flange, with the thicker part up, and toss it up into the air so that it flips over and over. The game was played by two or more players, each for them self or by sides.
Small Number (curiously): “So what was the point of the game?”

Auntie (approvingly): “Good question, Small Number! If the die fell upon either side face the opponent took it; if on the long back face or on the concave top face, it counted it one for who threw it; if on the bottom, it counted two; or if on the front face, it counted four.”
Small Number (still curiously): “Do you know what the winner would get?”
Auntie (smiling): “The winner had the privilege of smearing the loser's face with soot.”
Small Number (laughing): “I would love to smear my friends' faces with soot if I won the game. That would be so much fun!”

Auntie (seriously): “I am curious if you are able to relate this game to anything that you have learned in your math class?”
Small Number (scratching his head): “Well, you mentioned the numbers one, two, and four. There are different shapes of different faces there; the bottom looks like a rectangle; the front looks like a square to me; and the side looks like… I don't remember what it is called, but it does not look like rectangle because the parallel sides seem to be of different lengths. And you used a word that I didn't understand, but sounded like something that my math teacher would say. You didn't mention the number zero. Is this little circle on your drawing the letter ‘o’ or the number zero? Are we allowed to mix letters and numbers when we do math?”


Auntie (nodding her head): “Very good, Small Number, you make me feel proud. And you are right, the book in which I found this drawing, says that this symbol is the letter ‘o’. But there is more of what I would call math in this game. First, just as when you play your game with your friends, in this game there is a set of rules that every player needs to follow. For example, if the die lands on either side face, the other player takes a turn. This is something that we do in math all the time. Can you think about a mathematical rule that you need to follow when you calculate something?”
Small Number (quietly): “I don't know… Wait, I know: I need to do times before I do plus.”
Auntie (smiling): “I would say that differently, but that is the rule! But there is more mathematics that we can think about when we talk about the Throwing Game. For example, you see that after tossing the die, it can land on one of its six faces. So, there are six different possible outcomes. One may ask what is the chance that, without cheating, the die would land on the front face? Or any other face? Can we, somehow, come up with a number that would tell us the likelihood that a particular outcome will happen? How would you call and establish such a number? I think that you will learn in Grade 12 that the branch of mathematics that study this kind of questions is called probability.”

Small Number (confused): “Auntie, I have no idea what you are talking about. But I think that there are only four outcomes in your drawing: o, 1, 2 and 4.”
Auntie (lovingly): “Good thinking, Small Number. Yes, the creators of this game decided to associate the same symbol to different outcomes in two cases. You will learn in high school that this is an important thing in mathematics: that each side is assigned a single symbol, but more than one side may be assigned the same symbol. But there is something that really intrigues me here. I am not surprised that the sides of the die are assigned the same symbol ‘o’, as they are the only symmetric faces of the die. Otherwise, the die seems to be asymmetric. So why is the same value assigned for the back of the die and the L-shaped top of the die? Did the Haida ancestors, after tossing the die many times, conclude that the likelihood of the die landing on either of those sides is the same? Or did they do that to tease the players? Or for some other reason? We will never know…”

Auntie (thoughtfully): “One could ask what is the probability that the outcome will be 1? Or the probability that the other player takes the die? Actually, I wonder if the Haida people at that time used numbers? I used the description of the game that was written by a young anthropologist who spent a year living with the Haida people many, many, many, years ago. Maybe he decided to use numbers to label the outcomes because that is another use of symbols that we call numerals? Maybe the ancestors used something else?”
Small Number (standing up): “I don't know anything about numerals. Is a numeral something different than a number? I love you Auntie and this is all very interesting, but I have to run home to do my math homework, otherwise my mom will not let me play my game.”

Small Number (at the open door, turning his upper body towards Auntie): “Do you know how the players kept score in the game?”
