Tuberculosis

Spatial Statistical Analysis:
Point Pattern Analysis

Nearest Neighbour Analysis

Nearest neighbour analysis compares the observed average distances between nearest neighbouring points and those of a known pattern. The nearest neighbour statistic, or the R-scale, is calculated by dividing the observed average distance between nearest neighbours by the expected average distance between nearest neighbours. The R scale ranges from 0 (completely clustered) to 1 (random) to a maximum of 2.149 (completely dispersed).

Ordered neighbour statistics were calculated for each of the municipality to test whether the point pattern, i.e. the spatial distribution of TB cases, is dispersed, random, or clustered. Four statistical values were generated for each municipality in the table below: 1) Observed neighbour distance, 2) Expected neighbour distance, 3) The nearest neighbour statistic, and 4) The standardized Score.

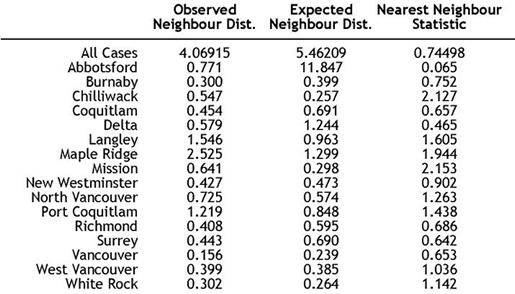
If Nearest Neighbour Analysis is applied to all the TB cases in the study area, the observed neighbour distance is 4.07 and the expected neighbour distance is 5.46. This results in a nearest neighbour statistic of 0.74 - the point pattern is more clustered than random. However, since the ZR is in between -1.96 and +1.96 (the critical values at the 0.05 significance level), the observed pattern is not significantly different from a random pattern. The disadvantage of analyzing the entire point pattern at the same time is that clustering at the local scale is undermined.

The following municipalities have a Nearest Neighbour statistic falling between 0 and 1, which indicates that the spatial distribution of TB cases in these municipalities is more clustered than random. They are listed in increasing level of clustering:

- New Westminster (0.902)
- Burnaby (0.752)
- Richmond (0.686)
- Coquitlam (0.657)
- Vancouver (0.653)
- Surrey (0.642)
- Delta (0.465)
- Abbotsford (0.065)

Ordered neighbour statistics are also applied to four clusters identified on the basis of distinct genetic fingerprints. While these cases are genetically clustered, it is important to discern whether or not they are also spatially clustered. Ordered neighbour statistics were applied to point patterns with Cluster ID 13, 14, 33, 35, and the point pattern with no cluster ID.

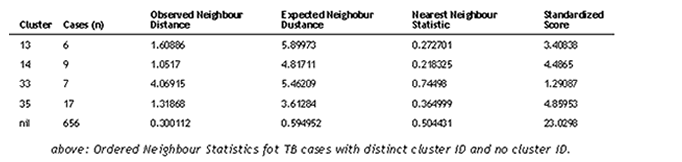
Cluster ID 14, which has 9 cases, is the most clustered, as indicated by a Nearest Neighbour Statistic of 0.218. Having a Nearest Neighbour Statistic between 0 and 1, Cluster IDs 13, 33, and 35 also show a more clustered than random point pattern. But for Cluster ID 33, because its Z score is within the range of -1.96 and +1.96, the observed point pattern is not significantly different from a random pattern (assuming a 0.05 significance level). For observations with no cluster ID, the pattern is also more clustered than random since the observed neighbour distance is less than the expected neighbour distance and the Nearest Neighbour Statistic is less than 1.

Quadrat Analysis

Quadrat analysis examines the change in density of point pattern over space to see whether the spatial distribution is more clustered or dispersed than a theoretically constructed random pattern. By overlaying the study area with a regular square grid, the frequency distribution of the number of squares with a given number of points can be calculated.

The variance-mean ratio (VMR) is used to standardize the degree of variability in cell frequencies relative to the mean cell frequency. Thus, a random point pattern would have a VMR of 1 or very close to 1. If an observed point pattern has a VMR of greater than 1, then it is more clustered than random. If an observed point pattern has a VMR of less than 1, then it is more dispersed than random. Other than comparing the ratio to 1, the difference has to be standardized by the standard error in order to determine if the standardized score of the difference is larger than the critical value (1.96 at the 0.05 level of significance).

Municipalities with a more clustered than random TB spatial distribution are Abbotsford, Coquitlam, Delta, Langley, Maple Ridge, Richmond, Surrey, Vancouver, West Vancouver, and White Rock. In particular, the TB cases in Abbotsford and Vancouver are highly clustered as indicated by their extremely large VMR.

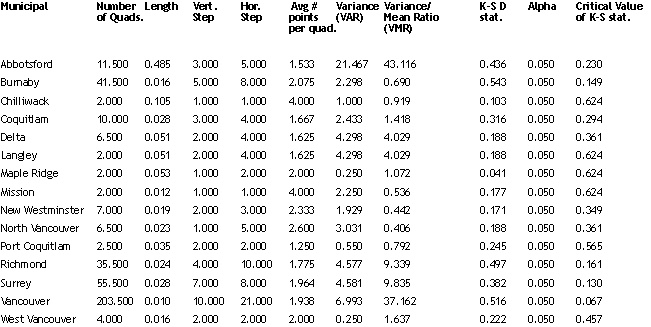
Quadrat Analysis Results for TB Point Pattern in All Municipalities

The Kolmogorov-Simirnov test, or the K-S D statistic, is used to statistically test the difference between an observed frequency distribution and a theoretical frequency distribution. If the calculated D is greater than the critical value of D at the same level of alpha, then the two distributions are significantly different statistically, i.e. the observed pattern is significantly different from a dispersed pattern. The TB point pattern in the following municipalities has a K-S D statistic of greater than the critical value, which implies that the point pattern is not dispersed: Abbotsford, Burnaby, Coquitlam, Richmond, Surrey, and Vancouver.

For some municipalities, the K-S test and the variance-mean ratio yield inconsistent results. In the case of Burnaby, VMR is less than 1 (pattern is more dispersed than random) but the K-S D statistic is greater than the critical value (pattern is significantly different from dispersed pattern). Because the K-S test is based upon weak-ordered data while variance-mean ratio is based upon an interval scale, the variance-mean ratio tends to be a stronger test (Lee and Wong, 2000, 69).

Previous - Next

Methodology & Analysis
Visualization | Demographic Profiling | MCE | Spatial Statistics [ 1 2 3 4 ]