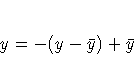MODEL Statement

The TRANSREG Procedure

MODEL Statement

MODEL < transform(dependents < / t-options >)
                     < transform(dependents < / t-options >)...> = >
                     transform(independents < / t-options >)
                     < transform(independents < / t-options >)...> < / a-options > ;

The MODEL statement specifies the dependent and independent variables (dependents and independents, respectively) and specifies the transformation (transform) to apply to each variable. Only one MODEL statement can appear in the TRANSREG procedure. The t-options are transformation options, and the a-options are the algorithm options. The t-options provide details for the transformation; these depend on the transform chosen. The t-options are listed after a slash in the parentheses that enclose the variable list (either dependents or independents). The a-options control the algorithm used, details of iteration, details of how the intercept and dummy variables are generated, and displayed output details. The a-options are listed after the entire model specification (the dependents, independents, transformations, and t-options) and after a slash. You can also specify the algorithm options in the PROC TRANSREG statement. When you specify the DESIGN o-option, dependents and an equal sign are not required. The operators "*", "|", and "@" from the GLM procedure are available for interactions with the CLASS expansion and the IDENTITY transformation.

      Class(a * b ...
            c | d ...
            e | f ... @ n)
   Identity(a * b ...
            c | d ...
            e | f ... @ n)

In addition, transformations and spline expansions can be crossed with classification variables:

   transform(var) * class(group)
   transform(var) | class(group)

See the "Types of Effects" section in Chapter 30, "The GLM Procedure," for a description of the @, *, and | operators and see the "Model Statement Usage" section for information on how to use these operators in PROC TRANSREG. Note that nesting is not allowed in PROC TRANSREG.

The next three sections discuss the transformations available ( transforms) (see the "Families of Transformations" section), the transformation options (t-options) (see the "Transformation Options (t-options)" section), and the algorithm options (a-options) (see the "Algorithm Options (a-options)" section).

Families of Transformations

In the MODEL statement, transform specifies a transformation in one of four families.

Variable expansions: preprocess the specified variables, replacing them with more variables.
Nonoptimal transformations: preprocess the specified variables, replacing each one with a single new nonoptimal, nonlinear transformation.
Optimal transformations: replace the specified variables with new, iteratively derived optimal transformation variables that fit the specified model better than the original variable (except for contrived cases where the transformation fits the model exactly as well as the original variable).
Other transformations: are the IDENTITY and SSPLINE transformations. These do not fit into the preceding categories.

The following table summarizes the transformations in each family.

	Members
Family	of Family
Variable expansions
B-spline basis	BSPLINE
set of dummy variables	CLASS
elliptical response surface	EPOINT
circular response surface	POINT
piecewise polynomial basis	PSPLINE
quadratic response surface	QPOINT
Nonoptimal transformations
inverse trigonometric sine	ARSIN
exponential	EXP
logarithm	LOG
logit	LOGIT
raises variables to specified power	POWER
transforms to ranks	RANK
noniterative smoothing spline	SMOOTH
Optimal transformations
linear	LINEAR
monotonic, ties preserved	MONOTONE
monotonic B-spline	MSPLINE
optimal scoring	OPSCORE
B-spline	SPLINE
monotonic, ties not preserved	UNTIE
Other transformations
identity, no transformation	IDENTITY
iterative smoothing spline	SSPLINE

You can use any transformation with either dependent or independent variables (except the SMOOTH transformation, which can be used only with independent variables). However, the variable expansions are usually more appropriate for independent variables.

The transform is followed by a variable (or list of variables) enclosed in parentheses. Optionally, depending on the transform, the parentheses can also contain t-options, which follow the variables and a slash. For example,

   model log(y)=class(x);

finds a LOG transformation of Y and performs a CLASS expansion of X.

   model identity(y) = spline(x1 x2 / nknots=3);

The preceding statement finds SPLINE transformations of X1 and X2. The NKNOTS= t-option used with the SPLINE transformation specifies three knots. The IDENTITY(Y) transformation specifies that Y is not to be transformed.

The rest of this section provides syntax details for members of the four families of transformations. The t-options are discussed in the "Transformation Options (t-options)" section.

Variable Expansions

The TRANSREG procedure performs variable expansions before iteration begins. Variable expansions expand the original variables into a typically larger set of new variables. The original variables are those that are listed in parentheses after transform, and they are sometimes referred to by the name of the transform. For example, in CLASS(X1 X2), X1 and X2 are sometimes referred to as CLASS expansion variables or simply CLASS variables, and the expanded variables are referred to as dummy variables. Similarly, in POINT(Dim1 Dim2), Dim1 and Dim2 are sometimes referred to as POINT variables.

The resulting variables are not transformed by the iterative algorithms after the initial preprocessing. Observations with missing values for these types of variables are excluded from the analysis.

The POINT, EPOINT, and QPOINT variable expansions are used in preference mapping analyses (also called PREFMAP, external unfolding, ideal point regression) (Carroll 1972) and for response surface regressions. These three expansions create circular, elliptical, and quadratic response or preference surfaces (see the "Point Models" section). The CLASS variable expansion is used for main effects ANOVA.

The following list provides syntax and details for the variable expansion transforms.

BSPLINE
BSP: expands each variable to a B-spline basis. You can specify the DEGREE=, KNOTS=, NKNOTS=, and EVENLY t-options with the BSPLINE expansion. When DEGREE=n (3 by default) with k knots (0 by default), n+k+1 variables are created. In addition, the original variable appears in the OUT= data set before the ID variables. For example, BSPLINE(X) expands X into X_0 X_1 X_2 X_3 and outputs X as well. The X_: variables contain the B-spline (which are the same basis vectors that the SPLINE and MSPLINE transformations use internally). The columns of the BSPLINE expansion sum to a column of ones, so an implicit intercept model is fit when the BSPLINE expansion is specified. If you specify the BSPLINE expansion for more than one variable, the model is less than full rank. See the section "SPLINE, BSPLINE, and PSPLINE Comparisons". Variables following BSPLINE must be numeric, and they are typically continuous.
CLASS
CLA: expands the variables to a set of dummy variables. For example, CLASS(X1 X2) is used for a simple main-effects model, CLASS(X1 | X2) fits a main-effects and interactions model, and CLASS(X1|X2|X3|X4@2 X1*X2*X3) creates all main effects, all two-way interactions, and one three-way interaction. See the "Model Statement Usage" section for information on how to use the operators @, *, and | in PROC TRANSREG. To determine class membership, PROC TRANSREG uses the values of the formatted variables. Variables following CLASS can be either character or numeric; numeric variables should be discrete.
EPOINT
EPO: expands the variables for an elliptical response surface regression or for an elliptical ideal point regression. Specify the COORDINATES o-option to output PREFMAP ideal elliptical point model coordinates to the OUT= data set. Each axis of the ellipse (or ellipsoid) is oriented in the same direction as one of the variables. The EPOINT expansion creates a new variable for each original variable. The value of each new variable is the square of each observed value for the corresponding parenthesized variable. The regression analysis then uses both sets of variables (original and squared). Variables following EPOINT must be numeric, and they are typically continuous.
POINT
POI: expands the variables for a circular response surface regression or for a circular ideal point regression. Specify the COORDINATES o-option to output PREFMAP ideal point model coordinates to the OUT= data set. The POINT expansion creates a new variable having a value for each observation that is the sums of squares of all the POINT variables. This new variable is added to the set of variables and is used in the regression analysis. For more on ideal point regression, refer to Carroll (1972). Variables following POINT must be numeric, and they are typically continuous.
PSPLINE
PSP: expands each variable to a piecewise polynomial basis. You can specify the DEGREE=, KNOTS=, NKNOTS=, and EVENLY t-options with PSPLINE. When DEGREE=n (3 by default) with k knots (0 by default), n+k variables are created. In addition, the original variable appears in the OUT= data set before the ID variables. For example, PSPLINE(X / NKNOTS=1) expands X into X_1 X_2 X_3 X_4 and outputs X as well. Unlike BSPLINE, an intercept is not implicit in the columns of PSPLINE. Refer to Smith (1979) for a good introduction to piecewise polynomial splines. Also see the section "SPLINE, BSPLINE, and PSPLINE Comparisons". Variables following PSPLINE must be numeric, and they are typically continuous.
QPOINT
QPO: expands the variables for a quadratic response surface regression or for a quadratic ideal point regression. Specify the COORDINATES o-option to output PREFMAP quadratic ideal point model coordinates to the OUT= data set. For m QPOINT variables, m(m+1)/2 new variables are created containing the squares and crossproducts of the original variables. The regression analysis uses both sets (original and crossed). Variables following QPOINT must be numeric, and they are typically continuous.

Nonoptimal Transformations

Like variable expansions, nonoptimal transformations are computed before the iterative algorithm begins. Nonoptimal transformations create a single new transformed variable that replaces the original variable. The new variable is not transformed by the subsequent iterative algorithms (except for a possible linear transformation with missing value estimation).

The following list provides syntax and details for nonoptimal variable transformations.

ARSIN

ARS

finds an inverse trigonometric sine transformation. Variables following ARSIN must be numeric, in the interval $(-1.0 \leq {{\hv X}} \leq 1.0)$ , and they are typically continuous.

EXP

exponentiates variables (the variable X is transformed to a^X). To specify the value of a, use the PARAMETER= t-option. By default, a is the mathematical constant e = 2.718 .... Variables following EXP must be numeric, and they are typically continuous.

LOG

transforms variables to logarithms (the variable X is transformed to log_a(X)). To specify the base of the logarithm, use the PARAMETER= t-option. The default is a natural logarithm with base e = 2.718 .... Variables following LOG must be numeric and positive, and they are typically continuous.

LOGIT

finds a logit transformation on the variables. The logit of X is log(X/(1-X)). Unlike other transformations, LOGIT does not have a three-letter abbreviation. Variables following LOGIT must be numeric, in the interval (0.0 < X < 1.0), and they are typically continuous.

POWER

POW

raises variables to a specified power (the variable X is transformed to X^a). You must specify the power parameter a by specifying the PARAMETER= t-option following the variables:

   power(variable / parameter=number)

You can use POWER for squaring variables (PARAMETER=2), reciprocal transformations (PARAMETER=-1), square roots (PARAMETER=0.5), and so on. Variables following POWER must be numeric, and they are typically continuous.

RANK

RAN

transforms variables to ranks. Ranks are averaged within ties. The smallest input value is assigned the smallest rank. Variables following RANK must be numeric.

SMOOTH

SMO

is a noniterative smoothing spline transformation. You can specify the smoothing parameter with either the SM= or the PARAMETER= t-option. The default smoothing parameter is SM=0. Variables following SMOOTH must be numeric, and they are typically continuous. The SMOOTH transformation can be used only with independent variables. For more information, see the "Smoothing Splines" section.

Optimal Transformations

Optimal transformations are iteratively derived. Missing values for these types of variables can be optimally estimated (see the "Missing Values" section).

The following list provides syntax and details for optimal transformations.

LINEAR
LIN: finds an optimal linear transformation of each variable. For variables with no missing values, the transformed variable is the same as the original variable. For variables with missing values, the transformed nonmissing values have a different scale and origin than the original values. Variables following LINEAR must be numeric.
MONOTONE
MON: finds a monotonic transformation of each variable, with the restriction that ties are preserved. The Kruskal (1964) secondary least-squares monotonic transformation is used. This transformation weakly preserves order and category membership (ties). Variables following MONOTONE must be numeric, and they are typically discrete.
MSPLINE
MSP: finds a monotonically increasing B-spline transformation with monotonic coefficients (de Boor 1978; de Leeuw 1986) of each variable. You can specify the DEGREE=, KNOTS=, NKNOTS=, and EVENLY t-options with MSPLINE. By default, PROC TRANSREG uses a quadratic spline. Variables following MSPLINE must be numeric, and they are typically continuous.
OPSCORE
OPS: finds an optimal scoring of each variable. The OPSCORE transformation assigns scores to each class (level) of the variable. Fisher's (1938) optimal scoring method is used. Variables following OPSCORE can be either character or numeric; numeric variables should be discrete.
SPLINE
SPL: finds a B-spline transformation (de Boor 1978) of each variable. By default, PROC TRANSREG uses a cubic polynomial transformation. You can specify the DEGREE=, KNOTS=, NKNOTS=, and EVENLY t-options with SPLINE. Variables following SPLINE must be numeric, and they are typically continuous.
UNTIE
UNT: finds a monotonic transformation of each variable without the restriction that ties are preserved. The TRANSREG procedure uses the Kruskal (1964) primary least-squares monotonic transformation method. This transformation weakly preserves order but not category membership (it may untie some previously tied values). Variables following UNTIE must be numeric, and they are typically discrete.

Other Transformations

IDENTITY
IDE: specifies variables that are not changed by the iterations. Typically, the IDENTITY transformation is used with a simple variable list, such as IDENTITY(X1-X5). However, you can also specify interaction terms. For example, IDENTITY(X1 | X2) creates X1, X2, and the product X1*X2; and IDENTITY(X1 | X2 | X3) creates X1, X2, X1*X2, X3, X1*X3, X2*X3, and X1*X2*X3. See the "Model Statement Usage" section for information on how to use the operators @, *, and | in PROC TRANSREG.

The IDENTITY transformation is used for variables when no transformation and no missing data estimation are desired. However, the REFLECT t-option, the ADDITIVE a-option, and the TSTANDARD=Z, and TSTANDARD=CENTER options can linearly transform all variables, including IDENTITY variables, after the iterations. Observations with missing values in IDENTITY variables are excluded from the analysis, and no optimal scores are computed for missing values in IDENTITY variables. Variables following IDENTITY must be numeric.
SSPLINE
SSP: finds an iterative smoothing spline transformation of each variable. The SSPLINE transformation does not generally minimize squared error. You can specify the smoothing parameter with either the SM= t-option or the PARAMETER= t-option. The default smoothing parameter is SM=0. Variables following SSPLINE must be numeric, and they are typically continuous.

Transformation Options (t-options)

If you use a nonoptimal, optimal, or other transformation, you can use t-options, which specify additional details of the transformation. The t-options are specified within the parentheses that enclose variables and are listed after a slash. You can use t-options with both dependent and independent variables. For example,

   proc transreg;
      model identity(y)=spline(x / nknots=3);
      output;
   run;

The preceding statements find an optimal variable transformation (SPLINE) of the independent variable, and they use a t-option to specify the number of knots (NKNOTS=). The following is a more complex example:

   proc transreg;
      model mspline(y / nknots=3)=class(x1 x2 / effects);
      output;
   run;

These statements find a monotone spline transformation (MSPLINE with three knots) of the dependent variable and perform a CLASS expansion with effects coding of the independents.

The following sections discuss the t-options available for nonoptimal, optimal, and other transformations.

The following table summarizes the t-options.

Table 65.2: t-options Available in the MODEL Statement

Task	Option
Nonoptimal transformation t-options
uses original mean and variance	ORIGINAL
Parameter t-options
specifies miscellaneous parameters	PARAMETER=
specifies smoothing parameter	SM=
Spline t-options
specifies the degree of the spline	DEGREE=
spaces the knots evenly	EVENLY
specifies the interior knots or break points	KNOTS=
creates n knots	NKNOTS=
CLASS Variable t-options
CLASS dummy variable name prefix	CPREFIX=
requests a deviations-from-means coding	DEVIATIONS
requests a deviations-from-means coding	EFFECTS
CLASS dummy variable label prefix	LPREFIX=
order of class variable levels	ORDER=
CLASS dummy variable label separators	SEPARATORS=
controls reference levels	ZERO=
Other t-options
operations occur after the expansion	AFTER
renames variables	NAME=
reflects the variable around the mean	REFLECT
specifies transformation standardization	TSTANDARD=

Nonoptimal Transformation t-options

ORIGINAL
ORI: matches the variable's final mean and variance to the mean and variance of the original variable. By default, the mean and variance are based on the transformed values. The ORIGINAL t-option is available for all of the nonoptimal transformations.

Parameter t-options

PARAMETER=number
PAR=number: specifies the transformation parameter. The PARAMETER= t-option is available for the EXP, LOG, POWER, SMOOTH, and SSPLINE transformations. For EXP, the parameter is the value to be exponentiated; for LOG, the parameter is the base value; and for POWER, the parameter is the power. For SMOOTH and SSPLINE, the parameter is the raw smoothing parameter. (You can specify a SAS/GRAPH-style smoothing parameter with the SM= t-option.) The default for the PARAMETER= t-option for the LOG and EXP transformations is e = 2.718 .... The default parameter for SMOOTH and SSPLINE is computed from SM=0. For the POWER transformation, you must specify the PARAMETER= t-option; there is no default.
SM=n: specifies a SAS/GRAPH-style smoothing parameter in the range 0 to 100. You can specify the SM= t-option only with the SMOOTH and SSPLINE transformations. The smoothness of the function increases as the value of the smoothing parameter increases. By default, SM=0.

Spline t-options

The following t-options are available with the SPLINE and MSPLINE optimal transformations and the PSPLINE and BSPLINE expansions.

DEGREE=n

DEG=n

specifies the degree of the spline transformation. The degree must be a nonnegative integer. The defaults are DEGREE=3 for SPLINE, PSPLINE, and BSPLINE variables and DEGREE=2 for MSPLINE variables.

The polynomial degree should be a small integer, usually 0, 1, 2, or 3. Larger values are rarely useful. If you have any doubt as to what degree to specify, use the default.

EVENLY

EVE

is used with the NKNOTS= t-option to space the knots evenly. The differences between adjacent knots are constant.

If you specify NKNOTS=k, k knots are created at

minimum + i(( maximum - minimum) / (k + 1))

for i = 1, ... ,k. For example, if you specify

   spline(X / knots=2 evenly)

and the variable X has a minimum of 4 and a maximum of 10, then the two interior knots are 6 and 8. Without the EVENLY t-option, the NKNOTS= t-option places knots at percentiles, so the knots are not evenly spaced.

KNOTS=number-list | n TO m BY p

KNO=number-list | n TO m BY p

specifies the interior knots or break points. By default, there are no knots. The first time you specify a value in the knot list, it indicates a discontinuity in the nth (from DEGREE=n) derivative of the transformation function at the value of the knot. The second mention of a value indicates a discontinuity in the (n-1)th derivative of the transformation function at the value of the knot. Knots can be repeated any number of times for decreasing smoothness at the break points, but the values in the knot list can never decrease.

You cannot use the KNOTS= t-option with the NKNOTS= t-option. You should keep the number of knots small (see the section "Specifying the Number of Knots").

NKNOTS=n

NKN=n

creates n knots, the first at the 100/(n+1) percentile, the second at the 200/(n+1) percentile, and so on. Knots are always placed at data values; there is no interpolation. For example, if NKNOTS=3, knots are placed at the twenty-fifth percentile, the median, and the seventy-fifth percentile. By default, NKNOTS=0. The NKNOTS= t-option must be $\geq 0$ .

You cannot use the NKNOTS= t-option with the KNOTS= t-option.

You should keep the number of knots small (see the section "Specifying the Number of Knots").

CLASS Variable t-options

CPREFIX=n | number-list
CPR=n | number-list: specifies the number of first characters of a CLASS expansion variable's name to use in constructing names for dummy variables. When CPREFIX= is specified as an a-option (see the description of the CPREFIX= a-option) or an o-option, it specifies the default for all CLASS variables. When you specify CPREFIX= as a t-option, it overrides the default only for selected variables. A different CPREFIX= value can be specified for each CLASS variable by specifying the CPREFIX=number-list t-option, like the ZERO=formatted-value-list t-option.
DEVIATIONS
DEV
EFFECTS
EFF: requests a deviations-from-means coding of CLASS variables. The coded design matrix has values of 0, 1, and -1 for reference levels. This coding is referred to as "deviations-from-means," "effects," "center-point," or "full-rank" coding.
LPREFIX=n | number-list
LPR=n | number-list: specifies the number of first characters of a CLASS expansion variable's label (or name if no label is specified) to use in constructing labels for dummy variables. When LPREFIX= is specified as an a-option (see the description of the LPREFIX= a-option) or an o-option, it specifies the default for all CLASS variables. When you specify LPREFIX= as a t-option, it overrides the default only for selected variables. A different LPREFIX= value can be specified for each CLASS variable by specifying the LPREFIX=number-list t-option, like the ZERO=formatted-value-list t-option.
ORDER=DATA | FREQ | FORMATTED | INTERNAL
ORD=DAT | FRE | FOR | INT: specifies the order in which the CLASS variable levels are to be reported. The default is ORDER=INTERNAL. For ORDER=FORMATTED and ORDER=INTERNAL, the sort order is machine dependent. When ORDER= is specified as an a-option (see the description of the ORDER= a-option) or as an o-option, it specifies the default ordering for all CLASS variables. When you specify ORDER= as a t-option, it overrides the default ordering only for selected variables. You can specify a different ORDER= value for each CLASS specification.
SEPARATORS='string-1 '<'string-2 ' >
SEP='string-1 '<'string-2 ' >: specifies separators for creating CLASS expansion variable labels. By default, SEPARATORS=' ' ' * ' ("blank" and "blank asterisk blank"). When SEPARATORS= is specified as an a-option (see the description of the SEPARATORS= a-option) or an o-option, it specifies the default separators for all CLASS variables. When you specify SEPARATORS= as a t-option, it overrides the default only for selected variables. You can specify a different SEPARATORS= value for each CLASS specification.
ZERO=FIRST | LAST | NONE | SUM
ZER=FIR | LAS | NON | SUM
ZERO='formatted-value ' <'formatted-value ' ...>: is used with CLASS variables. The default is ZERO=LAST.

The specification CLASS(variable / ZERO=FIRST) sets to missing the dummy variable for the first of the sorted categories, implying a zero coefficient for that category.

The specification CLASS(variable / ZERO=LAST) sets to missing the dummy variable for the last of the sorted categories, implying a zero coefficient for that category.

The specification CLASS(variable / ZERO='formatted-value') sets to missing the dummy variable for the category with a formatted value that matches 'formatted-value', implying a zero coefficient for that category. With ZERO=formatted-value-list, the first formatted value applies to the first variable in the specification, the second formatted value applies to the next variable that was not previously mentioned and so on. For example, CLASS(A A*B B B*C C / ZERO='x' 'y' 'z') specifies that the reference level for A is 'x', for B is 'y', and for C is 'z'. With ZERO='formatted-value', the procedure first looks for exact matches between the formatted values and the specified value. If none are found, leading blanks are stripped from both and the values are compared again. If zero or two or more matches are found, warnings are issued.

The specifications ZERO=FIRST, ZERO=LAST, and ZERO='formatted-value' are used for reference cell models. The Intercept parameter estimate is the marginal mean for the reference cell, and the other marginal means are obtained by adding the intercept to the dummy variable coefficients.

The specification CLASS(variable / ZERO=NONE) sets to missing none of the dummy variables. The columns of the expansion sum to a column of ones, so an implicit intercept model is fit. If you specify ZERO=NONE for more than one variable, the model is less than full rank. In the model MODEL IDENTITY(Y) = CLASS(X / ZERO=NONE), the coefficients are cell means.

The specification CLASS(variable / ZERO=SUM) sets to missing none of the dummy variables, and the coefficients for the dummy variables created from the variable sum to 0. This creates a less-than-full-rank model, but the coefficients are uniquely determined due to the sum-to-zero constraint.

In the presence of iterative transformations, hypothesis tests for ZERO=NONE and ZERO=SUM levels are not exact; they are liberal because a model with an explicit intercept is fit inside the iterations. There is no provision for adjusting the transformations while setting to 0 a parameter that is redundant given the explicit intercept and the other parameters.

Other t-options

AFTER

AFT

requests that certain operations occur after the expansion. This t-option affects the NKNOTS= t-option when the SPLINE or MSPLINE transformation is crossed with a CLASS specification. For example, if the original spline variable (1 2 3 4 5 6 7 8 9) is expanded into the three variables (1 2 3 0 0 0 0 0 0), (0 0 0 4 5 6 0 0 0), and (0 0 0 0 0 0 7 8 9), then, by default, NKNOTS=1 would use the overall median of 5 as the knot for all three variables. When you specify the AFTER t-option, the knots for the three variables are 2, 5, and 8. Note that the structural zeros are ignored when the internal knot list is created, but they are not ignored for the external knots.

You can also specify the AFTER t-option with the RANK and SMOOTH transformations. The following specifications compute ranks and smooth within groups, after crossing, ignoring the structural zeros.

   class(x / zero=none) | rank(z / after)
   class(x / zero=none) | smooth(z / after)

NAME=(variable-list)

NAM=(variable-list)

renames variables as they are used in the MODEL statement. This t-option allows a variable to be used more than once.

For example, if X is a character variable, then the following step stores both the original character variable X and a numeric variable XC that contains category numbers in the OUT= data set.

   proc transreg data=a;
      model identity(y) = opscore(x / name=(xc));
      output;
      id x;
   run;

With the CLASS and IDENTITY transformations, which allow interaction effects, the first name applies to the first variable in the specification, the second name applies to the next variable that was not previously mentioned, and so on. For example, IDENTITY(A A*B B B*C C / NAME=(G H I)) specifies that the new name for A is G, for B is H, and for C is I. The same assignment is used for the (not useful) specification IDENTITY(A A B B C C / NAME=(G H I)). For all transforms other than CLASS and IDENTITY (all those in which interactions are not supported), repeated variables are not handled specially. For example, SPLINE(A A B B C C / NAME=(A G B H C I)) creates six variables, a copy of A named A, another copy of A named G, a copy of B named B, another copy of B named H, a copy of C named C, and another copy of C named I.

REFLECT

REF

reflects the transformation

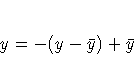
$y = -(y-\bar{y}) + \bar{y}$

after the iterations are completed and before the final standardization and results calculations. This t-option is particularly useful with the dependent variable in a conjoint analysis. When the dependent variable consists of ranks with the most preferred combination assigned 1.0, the REFLECT t-option reflects the transformation so that positive utilities mean high preference. (See Example 65.2.)

TSTANDARD=CENTER | NOMISS | ORIGINAL | Z

TST=CEN | NOM | ORI | Z

specifies the standardization of the transformed variables for the hypothesis tests and in the OUT= data set. By default, TSTANDARD=ORIGINAL. When TSTANDARD= is specified as an a-option (see the description of the TSTANDARD= a-option) or an o-option, it determines the default standardization for all variables. When you specify TSTANDARD= as a t-option, it overrides the default standardization only for selected variables. You can specify a different TSTANDARD= value for each transformation. For example, to perform a redundancy analysis with standardized dependent variables, specify

   model identity(y1-y4 / tstandard=z) = identity(x1-x10);

Algorithm Options (a-options)

This section discusses the options that can appear in the PROC TRANSREG or MODEL statements as a-options. They are listed after the entire model specification and after a slash.

For example,

   proc transreg;
      model spline(y / nknots=3)=log(x1 x2 / parameter=2)
            / nomiss maxiter=50;
      output;
   run;

In the preceding statements, NOMISS and MAXITER= are a-options. (SPLINE and LOG are transforms, and NKNOTS= and PARAMETER= are t-options.) The statements find a spline transformation with 3 knots on Y and a base 2 logarithmic transformation on X1 and X2. The NOMISS a-option excludes all observations with missing values, and the MAXITER= a-option specifies the maximum number of iterations.

Table 65.3: Options Available in the PROC TRANSREG or MODEL Statements

Task	Option
Input data set
specifies input observation type	TYPE=
restarts iterations	REITERATE
Specify method and control iterations
specifies minimum criterion change	CCONVERGE=
specifies minimum data change	CONVERGE=
specifies canonical dummy-variable initialization	DUMMY
specifies maximum number of iterations	MAXITER=
specifies iterative algorithm	METHOD=
specifies number of canonical variables	NCAN=
specifies singularity criterion	SINGULAR=
Control missing data handling
includes monotone special missing values	MONOTONE=
excludes observations with missing values	NOMISS
unties special missing values	UNTIE=
Control intercept and CLASS variables
CLASS dummy variable name prefix	CPREFIX=
CLASS dummy variable label prefix	LPREFIX=
no intercept or centering	NOINT
order of class variable levels	ORDER=
controls output of reference levels	REFERENCE=
CLASS dummy variable label separators	SEPARATORS=
Control displayed output
confidence limits alpha	ALPHA=
displays parameter estimate confidence limits	CL
displays model specification details	DETAIL
displays iteration histories	HISTORY
suppresses displayed output	NOPRINT
suppresses the iteration histories	SHORT
displays regression results	SS2
displays ANOVA table	TEST
displays conjoint part-worth utilities	UTILITIES
Control standardization
fits additive model	ADDITIVE
do not zero constant variables	NOZEROCONSTANT
specifies transformation standardization	TSTANDARD=

The following list provides details on these a-options.

ADDITIVE

ADD

creates an additive model by multiplying the values of each independent variable (after the TSTANDARD= standardization) by that variable's corresponding multiple regression coefficient. This process scales the independent variables so that the predicted-values variable for the final dependent variable is simply the sum of the final independent variables. An additive model is a univariate multiple regression model. As a result, the ADDITIVE a-option is not valid if METHOD=CANALS, or if METHOD=REDUNDANCY or METHOD=UNIVARIATE with more than one dependent variable.

ALPHA=number

ALP=number

specifies the level of significance for all of the confidence limits. By default, ALPHA=0.05.

CCONVERGE=n

CCO=n

specifies the minimum change in the criterion being optimized (squared multiple correlation for METHOD=MORALS and METHOD=UNIVARIATE, average squared multiple correlation for METHOD=REDUNDANCY, average squared canonical correlation for METHOD=CANALS) that is required to continue iterating. By default, CCONVERGE=0.0.

CL

requests confidence limits on the parameter estimates in the displayed output.

CONVERGE=n

CON=n

specifies the minimum average absolute change in standardized variable scores that is required to continue iterating. By default, CONVERGE=0.00001. Average change is computed over only those variables that can be transformed by the iterations; that is, all LINEAR, OPSCORE, MONOTONE, UNTIE, SPLINE, MSPLINE, and SSPLINE variables and nonoptimal transformation variables with missing values.

CPREFIX=n

CPR=n

specifies the number of first characters of a CLASS expansion variable's name to use in constructing names for dummy variables. Dummy variable names are constructed from the first n characters of the CLASS expansion variable's name and the first 32 - n characters of the formatted CLASS expansion variable's value. For example, if the variable ClassVariable has values 1, 2, and 3, then, by default, the dummy variables are named ClassVariable1, ClassVariable2, and ClassVariable3. However, with CPREFIX=5, the dummy variables are named Class1, Class2, and Class3. When CPREFIX=0, dummy variable names are created entirely from the CLASS expansion variable's formatted values. Valid values range from -1 to 31, where -1 indicates the default calculation and 0 to 31 are the number of prefix characters to use. The default, -1, sets n to 32 - min(32, max(2, fl)), where fl is the format length. When CPREFIX= is specified as an a-option or an o-option, it specifies the default for all CLASS variables. When you specify CPREFIX= as a t-option, it overrides the default only for selected variables.

DETAIL

DET

reports on details of the model specification. For example, it reports the knots and coefficients for splines, reference levels for CLASS variables, and so on.

DUMMY

DUM

provides a canonical dummy variable initialization. When there are no monotonicity constraints and there is only one canonical variable in each set, PROC TRANSREG (with the DUMMY a-option) can usually find the optimal solution in only one iteration. The initialization iteration is number 0, which is slower and uses more memory than other iterations. However, when there are no monotonicity constraints, when there is only one canonical variable in each set, and when there is enough available memory, specifying the DUMMY a-option can greatly decrease the amount of time required to find the optimal transformations. Furthermore, by solving for the transformations directly instead of iteratively, PROC TRANSREG avoids certain nonoptimal solutions.

HISTORY

HIS

displays the iteration histories even when the NOPRINT a-option is specified.

LPREFIX=n

LPR=n

specifies the number of first characters of a CLASS expansion variable's label (or name if no label is specified) to use in constructing labels for dummy variables. Dummy variable labels are constructed from the first n characters of the CLASS expansion variable's name and the first 127 - n characters of the formatted CLASS expansion variable's value. Valid values range from -1 to 127. Values of 0 to 127 specify the number of name or label characters to use. The default is -1, which specifies that PROC TRANSREG should pick a value depending on the length of the prefix and the formatted class value. When LPREFIX= is specified as an a-option or an o-option, it determines the default for all CLASS variables. When you specify LPREFIX= as a t-option, it overrides the default only for selected variables.

MAXITER=n

MAX=n

specifies the maximum number of iterations. By default, MAXITER=30. A specification of MAXITER=0 is allowed to save time when no transformations are requested.

METHOD=CANALS | MORALS | REDUNDANCY | UNIVARIATE

MET=CAN | MOR | RED | UNI

specifies the iterative algorithm. By default, METHOD=UNIVARIATE, unless you specify options that cannot be handled by the UNIVARIATE algorithm. Specifically, the default is METHOD=MORALS for the following situations:

if you specify LINEAR, OPSCORE, MONOTONE, UNTIE, SPLINE, MSPLINE, or SSPLINE transformations for the independent variables
if you specify the ADDITIVE a-option with more than one dependent variable
if you specify the IAPPROXIMATIONS o-option

CANALS: specifies canonical correlation with alternating least squares. This jointly transforms all dependent and independent variables to maximize the average of the first n squared canonical correlations, where n is the value of the NCAN= a-option.
MORALS: specifies multiple optimal regression with alternating least squares. This transforms each dependent variable, along with the set of independent variables, to maximize the squared multiple correlation.
REDUNDANCY: jointly transforms all dependent and independent variables to maximize the average of the squared multiple correlations.
UNIVARIATE: transforms each dependent variable to maximize the squared multiple correlation, while the independent variables are not transformed.

MONOTONE=two-letters

MON=two-letters

specifies the first and last special missing value in the list of those special missing values to be estimated using within-variable order and category constraints. By default, there are no order constraints on missing value estimates. The two-letters value must consist of two letters in alphabetical order. For example, MONOTONE=DF means that the estimate of .D must be less than or equal to the estimate of .E, which must be less than or equal to the estimate of .F; no order constraints are placed on estimates of ._, .A through .C, and .G through .Z. For details, see the "Missing Values" section.

NCAN=n

NCA=n

specifies the number of canonical variables to use in the METHOD=CANALS algorithm. By default, NCAN=1. The value of the NCAN= a-option must be $\geq 1$ .

When canonical coefficients and coordinates are included in the OUT= data set, the NCAN= a-option also controls the number of rows of the canonical coefficient matrices in the data set. If you specify an NCAN= value larger than the minimum of the number of dependent variables and the number of independent variables, PROC TRANSREG displays a warning and sets the NCAN= a-option to the maximum allowable value.

NOINT

NOI

omits the intercept from the OUT= data set and suppresses centering of data. The NOINT a-option is not allowed with iterative transformations since there is no provision for optimal scaling without an intercept. The NOINT a-option is allowed only when there is no implicit intercept and when all of the data in a BY group absolutely will not change during the iterations.

NOMISS

NOM

excludes all observations with missing values from the analysis, but does not exclude them from the OUT= data set. If you omit the NOMISS a-option, PROC TRANSREG simultaneously computes the optimal transformations of the nonmissing values and estimates the missing values that minimize squared error. For details, see the "Missing Values" section.

Casewise deletion of observations with missing values occurs when the NOMISS a-option is specified, when there are missing values in expansions, when there are missing values in METHOD=UNIVARIATE independent variables, when there are weights less than or equal to 0, or when there are frequencies less than 1. Excluded observations are output with a blank value for the _TYPE_ variable, and they have a weight of 0. They do not contribute to the analysis but are scored and transformed as supplementary or passive observations.

See the "Passive Observations" section for more information on excluded observations.

NOPRINT

NOP

suppresses the display of all output unless you specify the HISTORY a-option. The NOPRINT a-option without the HISTORY a-option temporarily disables the Output Delivery System (ODS). For more information, see Chapter 15, "Using the Output Delivery System."

NOZEROCONSTANT

NOZERO

NOZ

specifies that constant variables are expected and should not be zeroed. By default, constant variables are zeroed. This option is useful when PROC TRANSREG is used to code designs for choice models. When these designs are very large, it may be more efficient to code by subject and choice set. When attributes are constant within choice set, specify the NOZEROCONSTANT option to get the correct results. You can specify this option in the PROC TRANSREG, MODEL, and OUTPUT statements.

ORDER=DATA | FREQ | FORMATTED | INTERNAL

ORD=DAT | FRE | FOR | INT

specifies the order in which the CLASS variable levels are to be reported. The default is ORDER=INTERNAL. For ORDER=FORMATTED and ORDER=INTERNAL, the sort order is machine dependent. When ORDER= is specified as an a-option or an o-option, it determines the default ordering for all CLASS variables. When you specify ORDER= as a t-option, it overrides the default ordering only for selected variables.

DATA: sorts by order of appearance in the input data set.
FORMATTED: sorts by formatted value.
FREQ: sorts by descending frequency count; levels with the most observations appear first.
INTERNAL: sorts by unformatted value.

REFERENCE=NONE | MISSING | ZERO

REF=NON | MIS | ZER

specifies how reference levels of CLASS variables are to be treated. The options are REFERENCE=NONE, the default, in which reference levels are suppressed; REFERENCE=MISSING, in which reference levels are displayed and output with missing values; and REFERENCE=ZERO, in which reference levels are displayed and output with zeros. The REFERENCE= option can be specified in the PROC TRANSREG, MODEL, or OUTPUT statement, and it can be independently specified for the OUT= data set and the displayed output. When you specify it in only one statement, it sets the option for both the displayed output and the OUT= data set.

REITERATE

REI

enables the TRANSREG procedure to use previous transformations as starting points. The REITERATE a-option affects only variables that are iteratively transformed (specified as LINEAR, OPSCORE, MONOTONE, UNTIE, SPLINE, MSPLINE, and SSPLINE). For iterative transformations, the REITERATE a-option requests a search in the input data set for a variable that consists of the value of the TDPREFIX= or TIPREFIX= o-option followed by the original variable name. If such a variable is found, it is used to provide the initial values for the first iteration. The final transformation is a member of the transformation family defined by the original variable, not the transformation family defined by the initialization variable. See the section "Using the REITERATE Algorithm Option".

SEPARATORS='string-1 '<'string-2 ' >

SEP='string-1 '<'string-2 ' >

specifies separators for creating CLASS expansion variable labels. By default, SEPARATORS=' ' ' * ' ("blank" and "blank asterisk blank"). The first value is used to separate variable names and values in interactions. The second value is used to separate interaction components. For example, the label for the dummy variable for the A=1 and B=2 cell is, by default, 'A 1 * B 2'. If SEPARATORS='=' 'x' is specified, then the label is 'A=1xB=2'. When SEPARATORS= is specified as an a-option or an o-option, it determines the default separators for all CLASS variables. When you specify SEPARATORS= as a t-option, it overrides the default only for selected variables.

SHORT

SHO

suppresses the iteration histories.

SINGULAR=n

SIN=n

specifies the largest value within rounding error of zero. By default, SINGULAR=1E-12. The TRANSREG procedure uses the value of the SINGULAR= a-option for checking 1-R² when constructing full-rank matrices of predictor variables, checking denominators before dividing, and so on. PROC TRANSREG computes the regression coefficients by sweeping with rational pivoting.

SS2

produces a regression table based on Type II sums of squares. Tests of the contribution of each transformation to the overall model are displayed and output to the OUTTEST= data set when you specify the OUTTEST= option. When you specify the SS2 a-option, the TEST a-option is implied. See the section "Hypothesis Tests". You can suppress the variable labels in the regression tables by specifying the NOLABEL option in the OPTIONS statement.

TEST

TES

generates an ANOVA table. PROC TRANSREG tests the null hypothesis that the vector of scoring coefficients for all of the transformations is zero. See the section "Hypothesis Tests".

TSTANDARD=CENTER | NOMISS | ORIGINAL | Z

TST=CEN | NOM | ORI | Z

specifies the standardization of the transformed variables for the hypothesis tests and in the OUT= data set. By default, TSTANDARD=ORIGINAL. When TSTANDARD= is specified as an a-option or an o-option, it determines the default standardization for all variables. When you specify TSTANDARD= as a t-option, it overrides the default standardization only for selected variables.

CENTER: centers the output variables to mean zero, but the variances are the same as the variances of the input variables.
NOMISS: sets the means and variances of the transformed variables in the OUT= data set, computed over all output values that correspond to nonmissing values in the input data set, to the means and variances computed from the nonmissing observations of the original variables. The TSTANDARD=NOMISS specification is useful with missing data. When a variable is linearly transformed, the final variable contains the original nonmissing values and the missing value estimates. In other words, the nonmissing values are unchanged. If your data have no

missing values, TSTANDARD=NOMISS and TSTANDARD=ORIGINAL produce the same results.
ORIGINAL: sets the means and variances of the transformed variables to the means and variances of the original variables. This is the default.
Z: standardizes the variables to mean zero, variance one.

The final standardization is affected by other options. If you also specify the ADDITIVE a-option, the TSTANDARD= option specifies an intermediate step in computing the final means and variances. The final independent variables, along with their means and standard deviations, are scaled by the regression coefficients, creating an additive model with all coefficients equal to one.

For nonoptimal variable transformations, the means and variances of the original variables are actually the means and variances of the nonlinearly transformed variables, unless you specify the ORIGINAL nonoptimal t-option in the MODEL statement. For example, if a variable X with no missing values is specified as LOG, then, by default, the final transformation of X is simply LOG(X), not LOG(X) standardized to the mean of X and variance of X.

TYPE='text '|name

TYP='text '|name

specifies the valid value for the _TYPE_ variable in the input data set. If PROC TRANSREG finds an input _TYPE_ variable, it uses only observations with a _TYPE_ value that matches the TYPE= value. This enables a PROC TRANSREG OUT= data set containing coefficients to be used as input to PROC TRANSREG without requiring a WHERE statement to exclude the coefficients. If a _TYPE_ variable is not in the data set, all observations are used. The default is TYPE='SCORE', so if you do not specify the TYPE= a-option, only observations with _TYPE_='SCORE' are used. Do not confuse this option with the data set TYPE= option. The DATA= data set must be an ordinary SAS data set.

PROC TRANSREG displays a note when it reads observations with blank values of _TYPE_, but it does not automatically exclude those observations. Data sets created by the TRANSREG and PRINQUAL procedures have blank _TYPE_ values for those observations that were excluded from the analysis due to nonpositive weights, nonpositive frequencies, or missing data. When these observations are read again, they are excluded for the same reason that they were excluded from their original analysis, not because their _TYPE_ value is blank.

UNTIE=two-letters

UNT=two-letters

specifies the first and last special missing value in the list of those special missing values that are to be estimated with within-variable order constraints but no category constraints. The two-letters value must consist of two letters in alphabetical order. By default, there are category constraints but no order constraints on special missing value estimates. For details, see the "Missing Values" section and the "Optimal Scaling" section.

UTILITIES

UTI

produces a table of the part-worth utilities from a conjoint analysis. Utilities, their standard errors, and the relative importance of each factor are displayed and output to the OUTTEST= data set when you specify the OUTTEST= qoption. When you specify the UTILITIES a-option, the TEST a-option is implied. Refer to SAS Technical Report R-109, Conjoint Analysis Examples, for more information on conjoint analysis.

Chapter Contents
Previous
Next
Top