Our goal in this lecture is to develop asymptotic distribution
theory for the sample autocorrelation function.
We let ![]() and
and
![]() be the ACF and estimated ACF
respectively.
be the ACF and estimated ACF
respectively.
We begin by reducing the behaviour of
![]() to the behaviour
of
to the behaviour
of ![]() , the sample autocovariance. Our approach is standard
Talyor expansion.
, the sample autocovariance. Our approach is standard
Talyor expansion.
Suppose you have pairs ![]() of random variables with
of random variables with
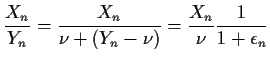
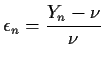
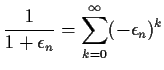
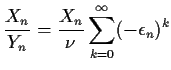
We want to compute the mean of this expression term by term and the
variance by using the formula for the variance of the sum and so on.
However, what we really do is truncate the infinite sum at some finite
number of terms and compute moments of the finite sum.
I want to be clear about the distinction; to do so I give an example.
Imagine that ![]() has a bivariate normal distribution with means
has a bivariate normal distribution with means
![]() , variances
, variances
![]() ,
, ![]() and
correlation
and
correlation ![]() between
between ![]() and
and ![]() . The quantity
. The quantity
![]() does not have a well defined mean because
E
does not have a well defined mean because
E![]() . Our expansion is
still valid, however. Stopping the sum at
. Our expansion is
still valid, however. Stopping the sum at ![]() leads to the approximation
leads to the approximation
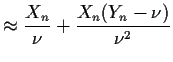 |
||
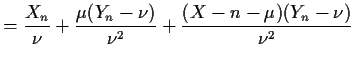 |
Definition: : If ![]() is a sequence of random variables and
is a sequence of random variables and ![]() a sequence of
constants then we write
a sequence of
constants then we write
The idea is that
![]() means that
means that ![]() is
proportional in size to
is
proportional in size to ![]() with the ``constant of
proportionality'' being a random variable which is not
likely to be too large. We also often have use for notation
indicating that
with the ``constant of
proportionality'' being a random variable which is not
likely to be too large. We also often have use for notation
indicating that ![]() is actually small compared to
is actually small compared to ![]() .
.
Definition: : We say
![]() if
if
![]() in probability:
for each
in probability:
for each
![]()
You can manipulate ![]() and
and ![]() notation algebraically with a few rules:
notation algebraically with a few rules:
These notions extend Landau's ![]() and
and ![]() notation to
random quantities.
notation to
random quantities.
Example: : In our ratio example we have
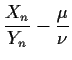 |
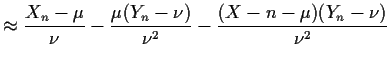 |
|
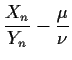 |
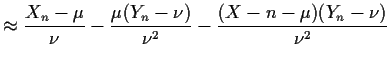 |
|
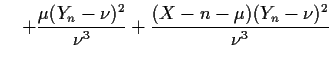 |
||
Keeping only terms of order
![]() we find
we find
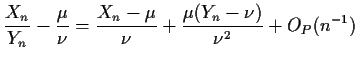
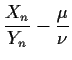
To keep terms up to order
![]() we have to keep terms out to
we have to keep terms out to ![]() (In general
(In general
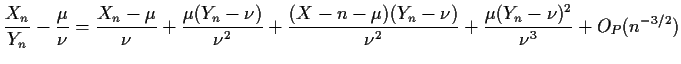
![$\displaystyle \left[\frac{X_n}{Y_n} -\frac{\mu}{\nu}\right] \approx$](img77.gif) E
E![$\displaystyle \left[\frac{X_n}{Y_n} -\frac{\mu}{\nu}\right] \approx
\rho\sigma\tau/n
$](img79.gif)
In order to compute the approximate variance we ought to compute the second moment
of
![]() and subtract the square of the first moment.
Imagine you had a random variable of the form
and subtract the square of the first moment.
Imagine you had a random variable of the form
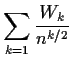
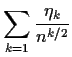
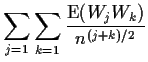
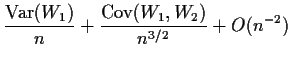
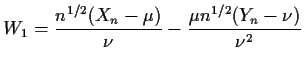
![$\displaystyle W_2 = - \frac{n^{1/2}(X_n-\mu) n^{1/2}(Y_n-\nu)}{\nu^2}
+
\frac{\mu[ n^{1/2}(Y_n-\nu)]^2}{\nu^3}
$](img87.gif)
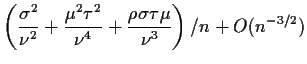
Now I want to apply these ideas to estimation of ![]() . We make
. We make
![]() be
be
![]() and
and ![]() be
be
![]() (and replace
(and replace ![]() by
by
![]() ). Our first order approximation to
). Our first order approximation to
![]() is
is
I now evaluate means and variances in the special case where ![]() has
been calculated using a known mean of 0. That is
has
been calculated using a known mean of 0. That is
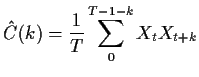
To compute the variance we begin with the second moment which is
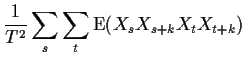
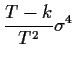
For ![]() and
and ![]() or
or ![]() the expectation is simply
the expectation is simply
![]() while for
while for ![]() we get
we get
![]() .
Thus the variance of the sample variance (when the mean is known
to be 0) is
.
Thus the variance of the sample variance (when the mean is known
to be 0) is
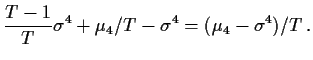
Having computed the variance it is usual to look at the large
sample distribution theory. For ![]() the usual central limit theorem
applies to
the usual central limit theorem
applies to
![]() (in the case of white noise) to prove that
(in the case of white noise) to prove that
For ![]() the theorem needed is called the
the theorem needed is called the ![]() -dependent central
limit theorem; it shows that
-dependent central
limit theorem; it shows that
The sample autocorrelation at lag ![]() is
is
It is possible to verify that subtraction of ![]() from the
observations before computing the sample covariances does not
change the large sample approximations, although it does affect
the exact formulas for moments.
from the
observations before computing the sample covariances does not
change the large sample approximations, although it does affect
the exact formulas for moments.
When the ![]() series is actually not white noise the situation is
more complicated. Consider as an example the model
series is actually not white noise the situation is
more complicated. Consider as an example the model
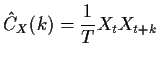
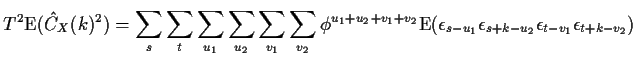
There are versions of the central limit theorem called
mixing central limit theorems which can be used for ARMA(![]() ) processes
in order to conclude that
) processes
in order to conclude that
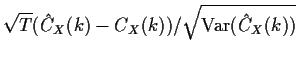
The general tactic is the ![]() method or Taylor expansion. In this
case for each sample size
method or Taylor expansion. In this
case for each sample size ![]() you have two estimates, say
you have two estimates, say ![]() and
and ![]() of two parameters. You want distribution theory for the ratio
of two parameters. You want distribution theory for the ratio
![]() . The idea is to write
. The idea is to write
![]() where
where
![]() and then make use of the fact that
and then make use of the fact that ![]() and
and ![]() are
close to the parameters they are estimates of. In our case
are
close to the parameters they are estimates of. In our case ![]() is the sample autocovariance at lag
is the sample autocovariance at lag ![]() which is close to the
true autocovariance
which is close to the
true autocovariance ![]() while the denominator
while the denominator ![]() is the
sample autocovariance at lag 0, a consistent estimator of
is the
sample autocovariance at lag 0, a consistent estimator of ![]() .
.
Write
Similar ideas can be used for the estimated sample partial ACF.
In order to test the hypothesis that a series is white noise using the
distribution theory just given, you have to produce a single statistic
to base youre test on. Rather than pick a single value of ![]() the
suggestion has been made to consider a sum of squares or a weighted
sum of squares of the
the
suggestion has been made to consider a sum of squares or a weighted
sum of squares of the
![]() .
.
A typical statistic is
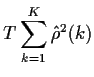
When the parameters in an ARMA(![]() ) have been estimated by maximum likelihood
the degrees of freedom must be adjusted to
) have been estimated by maximum likelihood
the degrees of freedom must be adjusted to ![]() . The resulting
test is the Box-Pierce test; a refined version which takes better account
of finite sample properties is the Box-Pierce-Ljung test. S-Plus plots the
. The resulting
test is the Box-Pierce test; a refined version which takes better account
of finite sample properties is the Box-Pierce-Ljung test. S-Plus plots the
![]() -values from these tests for 1 through 10 degrees of freedom as
part of the output of arima.diag.
-values from these tests for 1 through 10 degrees of freedom as
part of the output of arima.diag.