Non Gaussian series.
The fitting methods we have studied are based on the likelihood for a normal fit. However, the estimates work reasonably well even if the errors are not normal.
Example: AR(1) fit. We fit
![]() using
using
![]() which is consistent for non-Gaussian errors.
(In fact
which is consistent for non-Gaussian errors.
(In fact
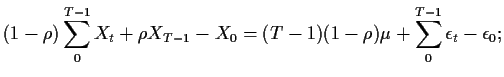
Here is an outline of the logic of what follows. We will assume that
the errors are iid mean 0, variance ![]() and finite fourth
moment
and finite fourth
moment
![]() E
E![]() . We will not assume that
the errors have a normal distribution.
. We will not assume that
the errors have a normal distribution.
![$\displaystyle B = \left[\begin{array}{cc}
\frac{1}{1-\rho^2} & 0 \\ 0 & \frac{ \mu_4-\sigma^4}{\sigma^6}
\end{array}\right]
$](img13.gif)
 E
E
![$\displaystyle A = \left[\begin{array}{cc}
\frac{1}{1-\rho^2} & 0 \\ 0 & \frac{2}{\sigma^2}
\end{array}\right]
$](img16.gif)

![$\displaystyle \hat\theta - \theta = \left[\frac{1}{T} I(\theta_0) \right]^{-1} \left[
T^{-1/2} U(\theta_0)\right] +$](img21.gif) negligible remainder
negligible remainder
![$\displaystyle \Sigma = A^{-1} B A^{-1} = \left[\begin{array}{cc}
1-\rho^2 & 0 \\ 0 & \frac{\mu_4-\sigma^4}{4\sigma^2}
\end{array}\right]
$](img24.gif)
Here are details.
Consistency: One of our many nearly equivalent
estimates of ![]() is
is
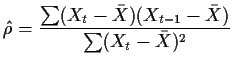
Score function: asymptotic normality
The score function is
![$\displaystyle U(\rho,\sigma) = \left[\begin{array}{c}
\frac{\sum X_{t-1}(X_t-\r...
...ac{\sum(X_t-\rho X_{t-1})^2}{\sigma^3}- \frac{T-1}{\sigma}
\end{array}\right]
$](img31.gif)
![$\displaystyle U(\rho,\sigma) = \left[\begin{array}{c}
\frac{\sum X_{t-1}\epsilo...
...\\
\frac{\sum \epsilon_t^2}{\sigma^3}- \frac{T-1}{\sigma}
\end{array}\right]
$](img32.gif)
To prove this assertion we define for each ![]() a martingale
a martingale
![]() for
for
![]() where
where
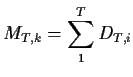
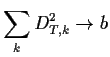
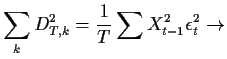 E
ESecond derivative matrix and Fisher information: the matrix of negative second derivatives is
![$\displaystyle -\frac{\partial U}{\partial\theta} = \left[\begin{array}{cc}
\fra...
...ac{\sum(X_t-\rho
X_{t-1})^2}{\sigma^4} -\frac{T-1}{\sigma^2}\end{array}\right]
$](img52.gif)
![$\displaystyle A= \left[\begin{array}{cc}
\frac{C(0)}{\sigma^2} & 0 \\ 0 & \frac{2}{\sigma^2}
\end{array}\right]
$](img53.gif)
Taylor expansion: In the next step we are supposed
to prove that a random vector has a MVN limit. The usual tactic to
prove this uses the so called Cramér-Wold device -- you prove that
each linear combination of the entries in the vector has a univariate
normal limit.
Then
![]() and Taylor's theorem is
that
and Taylor's theorem is
that
![$\displaystyle 0=U(\hat\rho,\hat\sigma) = U(\rho,\sigma) +
\left[\frac{\partial U(\theta)}{\partial\theta}\right] (\hat\theta -
\theta)
+R
$](img55.gif)
![$\displaystyle \left[\frac{\partial U(\theta)}{\partial\theta}\right] ^{-1}
$](img60.gif)
![$\displaystyle T^{1/2}(\hat\theta - \theta) = \left[-T^{-1}\frac{\partial
U(\theta)}{\partial\theta}\right] ^{-1} (T^{-1/2}U(\rho,\sigma) +T^{-1/2}R)
$](img61.gif)
![$\displaystyle \left[-T^{-1}\frac{\partial
U(\theta)}{\partial\theta}\right] ^{-1}(T^{-1/2}R)
\to 0
$](img62.gif)
Asymptotic normality: This is a consequence of
Slutsky's theorem applied to the Taylor expansion and the results
above for ![]() and
and ![]() . According to Slutsky's theorem the asymptotic
distribution of
. According to Slutsky's theorem the asymptotic
distribution of
![]() is the same as that
of
is the same as that
of
![$\displaystyle A^{-1} B (A^{-1})^t = \left[\begin{array}{cc}
1-\rho^2 & 0 \\ 0 & \frac{\mu_4-\sigma^4}{4\sigma^4}
\end{array}\right]
$](img68.gif)
Behaviour of ![]() : pick off the first component
and find
: pick off the first component
and find
Behaviour of
![]() : on the other hand
: on the other hand
More general models: For an ARMA![]() model the parameter
vector is
model the parameter
vector is
![$\displaystyle B=\left[\begin{array}{cc} B_1 & 0 \\ 0 & \frac{\mu_4-\sigma^4}{\sigma^6}
\end{array}\right]
$](img78.gif)
![$\displaystyle A = \left[\begin{array}{cc} A_1 & 0 \\ 0 & \frac{2}{\sigma^2}
\end{array}\right]
$](img79.gif)
Model assessment.
Having fitted an ARIMA model you get (essentially automatically)
fitted residuals
![]() . Most of the fitting methods lead to
fewer residuals than there were in the original series. Since the
parameter estimates are consistent (if the model fitted is correct,
of course) the fitted residuals should be essentially the true
. Most of the fitting methods lead to
fewer residuals than there were in the original series. Since the
parameter estimates are consistent (if the model fitted is correct,
of course) the fitted residuals should be essentially the true
![]() which is white noise. We will assess this by plotting the estimated
ACF of
which is white noise. We will assess this by plotting the estimated
ACF of
![]() and then seeing if the estimates are all close
enough to 0 to pass for white noise.
and then seeing if the estimates are all close
enough to 0 to pass for white noise.
To judge close enough we need asymptotic distribution theory for autocovariance estimates.