


Stat 804
Lecture 12 Notes
Large Sample Theory for Conditional Likelihood:
We have data 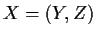 and study the conditional likelihood, score
Fisher information and mle:
and study the conditional likelihood, score
Fisher information and mle:
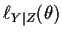 ,
,
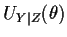 ,
,
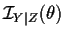 and
and
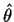 . In general standard maximum likelihood theory may
be expected to apply to these conditional objects:
. In general standard maximum likelihood theory may
be expected to apply to these conditional objects:
-
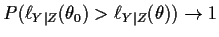 as the
``sample size'' (often measured by the Fisher information)
tends to infinity.
as the
``sample size'' (often measured by the Fisher information)
tends to infinity.
-
E
![$ _\theta\left[ U_{Y\vert Z}(\theta)\vert Z\right]=0$](img7.gif)
-
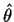 is consistent (converges to the true value as
the Fisher information converges to infinity).
is consistent (converges to the true value as
the Fisher information converges to infinity).
- The usual Bartlett identities hold. For example:
- The error in the mle has approximately the form
- The mle is approximately normal:
(where
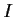 is the identity matrix).
is the identity matrix).
- The conditional Fisher information can be estimated by the observed information:
- The log-likelihood ratio is approximately
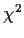 :
:
In the previous lecture I showed you 2) and 4) in this list.
Today we look at 5), 6) and 7) in the context of the 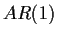 model
model
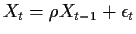 .
.



Richard Lockhart
2001-09-30
![]() and study the conditional likelihood, score
Fisher information and mle:
and study the conditional likelihood, score
Fisher information and mle:
![]() ,
,
![]() ,
,
![]() and
and
![]() . In general standard maximum likelihood theory may
be expected to apply to these conditional objects:
. In general standard maximum likelihood theory may
be expected to apply to these conditional objects:
![$\displaystyle _\theta\left[\frac{\partial}{\partial\theta} U_{Y\vert Z}(\theta)\vert Z\right]
$](img10.gif)
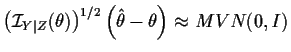
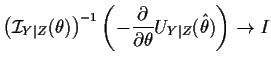
![]() model
model
![]() .
.