


Postscript version of these notes
STAT 804
Lecture 11
Likelihood Theory
First we review likelihood theory for conditional and full
maiximum likelihood estimation.
Suppose the data is 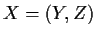 and write the density of
and write the density of 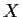 as
as
Differentiate the identity
with respect to 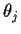 (the
(the 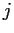 th component of
th component of 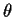 )
and pull the derivative under the integral sign to get
)
and pull the derivative under the integral sign to get
where
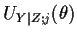 is the
is the 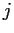 th component of
th component of
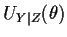 , the derivative of the log conditional
likelihood;
, the derivative of the log conditional
likelihood; 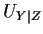 is called a conditional score. Since
is called a conditional score. Since
E
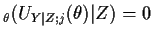
E
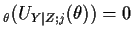
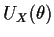 and
and
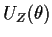 have mean 0 (when
have mean 0 (when 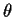 is the
true value of
is the
true value of 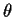 ).
Differentiate the identity a further time with respect to
).
Differentiate the identity a further time with respect to 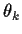 to get
We define the conditional Fisher information matrix
to get
We define the conditional Fisher information matrix
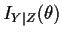 to have
to have 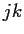 th entry
th entry
E
![$\displaystyle \left[- \frac{\partial^2 \ell}{\partial\theta_j\partial\theta_k}\vert Z\right]
$](img23.gif)
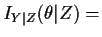
Var
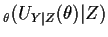
The corresponding identities based on 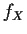 and
and 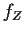 are
are
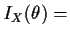
Var
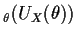
and
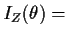
Var
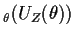
Now let's look at the model
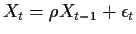 .
Putting
.
Putting
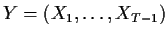 and
and 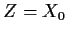 we find
we find
Differentiating again gives the matrix of second derivatives
Taking conditional expectations given 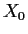 gives
To compute
gives
To compute
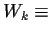 E
E![$ [X_k^2\vert X_0]$](img40.gif) write
write
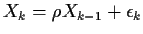 and get
with
and get
with 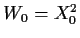 .
You can check carefully that in fact
.
You can check carefully that in fact 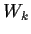 converges to some
converges to some 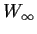 as
as
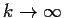 . This
. This 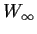 satisfies
satisfies
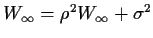 which gives
It follows that
Notice that although the conditional Fisher information
might have been expected to depend on
which gives
It follows that
Notice that although the conditional Fisher information
might have been expected to depend on 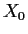 it does not, at least for
long series.
it does not, at least for
long series.



Richard Lockhart
2001-09-30
![]() and write the density of
and write the density of ![]() as
as
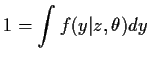
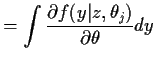
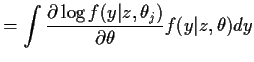
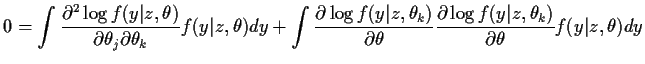
![$\displaystyle \left[- \frac{\partial^2 \ell}{\partial\theta_j\partial\theta_k}\vert Z\right]
$](img23.gif)
![]() and
and ![]() are
are
![]() .
Putting
.
Putting
![]() and
and ![]() we find
we find
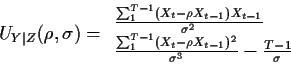
![\begin{displaymath}
\left[
\begin{array}{cc}
-\frac{\sum_1^{T-1}X_{t-1}^2}{\sigm...
...X_{t-1})^2}{\sigma^4} +\frac{T-1}{\sigma^2}
\end{array}\right]
\end{displaymath}](img36.gif)
![\begin{displaymath}
I_{Y\vert Z}(\rho,\sigma) = \left[
\begin{array}{cc}
\frac{\...
...gma^2}
&
0 \\ 0 &
\frac{2(T-1)}{\sigma^2}
\end{array}\right]
\end{displaymath}](img38.gif)
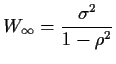
![\begin{displaymath}
\frac{1}{T} I_{Y\vert Z}(\rho,\sigma) \to
\left[
\begin{ar...
...{1}{1-\rho^2} & 0 \\ 0 & \frac{2}{\sigma^2}\end{array}\right]
\end{displaymath}](img49.gif)