Postscript version of these notes.

STAT 801 Lecture 18

Reading for Today's Lecture:

Goals of Today's Lecture:

• Discuss factorization criterion.

• Introduce completeness.

• Introduce the Lehman Scheffé theorem.

Finding Sufficient statistics

Binomial(n,p): log likelihood $\ell(\theta)$ (part depending on $\theta$) is function of X alone, not of $Y_1, \ldots,Y_n$ as well.

Normal example: $\ell(\mu)$ is, ignoring terms not containing $\mu$,

$$\ell(\mu) = \mu \sum X_i - n\mu^2/2 = n\mu\bar{X} -n\mu^2/2 \, .$$

Examples of the Factorization Criterion:

Theorem: If the model for data X has density $f(x,\theta)$then the statistic S(X) is sufficient if and only if the density can be factored as

$$f(x,\theta) = g(s(x),\theta)h(x)$$

Proof: Find statistic T(X) such that X is a one to one function of the pair S,T. Apply change of variables to the joint density of S and T. If the density factors then

$$f_{S,T}(s,t) =g(s,\theta) h(x(s,t))$$

so conditional density of T given S=s does not depend on $\theta$. Thus the conditional distribution of (S,T) given S does not depend on $\theta$ and finally the conditional distribution of X given S does not depend on $\theta$.

Conversely if S is sufficient then the f_T|S has no $\theta$ in it so joint density of S,T is

$$f_S(s,\theta) f_{T\vert S} (t\vert s)$$

Apply change of variables formula to get

$$f_X(x) = f_S(s(x),\theta) f_{T\vert S} (t(x)\vert s(x)) J(x)$$

where J is the Jacobian. This factors.

Example: If $X_1,\ldots,X_n$ are iid $N(\mu,\sigma^2)$then the joint density is
$$\begin{multline*}(2\pi)^{-n/2} \sigma^{-n} \times \\ \exp\{-\sum X_i^2/(2\sigma^2) +\mu\sum X_i/\sigma^2 -n\mu^2/(2\sigma^2)\} \end{multline*}$$
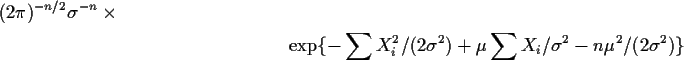
which is evidently a function of

$$\sum X_i^2, \sum X_i$$

This pair is a sufficient statistic. You can write this pair as a bijective function of $\bar{X}, \sum (X_i-\bar{X})^2$ so that this pair is also sufficient.

Completeness

In Binomial(n,p) example only one function of Xis unbiased. Rao Blackwell shows UMVUE, if it exists, will be a function of any sufficient statistic. Can there be more than one such function? Yes in general but no for some models like the binomial.

Definition: A statistic T is complete for a model $P_\theta;\theta\in\Theta$ if

$$E_\theta(h(T)) = 0$$

for all $\theta$ implies h(T)=0.

We have already seen that X is complete in the Binomial(n,p) model. In the $N(\mu,1)$ model suppose

$$E_\mu(h(\bar{X})) \equiv 0$$

Since $\bar{X}$ has a $N(\mu,1/n)$ distribution we find that

$$\int_{-\infty}^\infty h(x) e^{-x^2/2} e^{\mu x} dx \equiv 0$$

This is the so called Laplace transform of the function h(x)e^-x2/2. It is a theorem that a Laplace transform is 0 if and only if the function is 0 ( because you can invert the transform). Hence $h\equiv 0$.

How to Prove Completeness

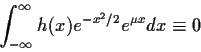
There is only one general tactic. Suppose X has density

$$f(x,\theta) = h(x) \exp\{\sum_1^p a_i(\theta)S_i(x)+c(\theta)\}$$

If the range of the function $(a_1(\theta),\ldots,a_p(\theta))$ as $\theta$ varies over $\Theta$ contains a (hyper-) rectangle in R^p then the statistic

$$( S_1(X), \ldots, S_p(X))$$

is complete and sufficient.

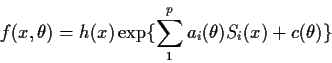
You prove the sufficiency by the factorization criterion and the completeness using the properties of Laplace transforms and the fact that the joint density of $S_1,\ldots,S_p$

$$g(s_1,\ldots,s_p;\theta) = h^*(s) \exp\{\sum a_k(\theta)s_k+c^*(\theta)\}$$

Example: $N(\mu,\sigma^2)$ model density has form

$$\frac{1}{\sqrt{2\pi}} \exp\left\{ \left(-\frac{1}{2\sigma^2}... ...rac{\mu}{\sigma^2} \right)x -\frac{\mu^2}{2\sigma^2} \right\}$$

which is an exponential family with

$$h(x) = \frac{1}{\sqrt{2\pi}}$$

$$a_1(\theta) = -\frac{1}{2\sigma^2}$$

S₁(x) = x²

$$a_2(\theta) = \frac{\mu}{\sigma^2}$$

S₂(x) = x

and

$$c(\theta) = -\frac{\mu^2}{2\sigma^2}$$

It follows that

$$(\sum X_i^2, \sum X_i)$$

is a complete sufficient statistic.

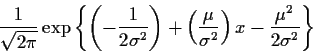
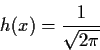
Remark: The statistic $(s^2, \bar{X})$ is a one to one function of $(\sum X_i^2, \sum X_i)$ so it must be complete and sufficient, too. Any function of the latter statistic can be rewritten as a function of the former and vice versa.

The Lehmann-Scheffé Theorem

Theorem: If S is a complete sufficient statistic for some model and h(S) is an unbiased estimate of some parameter $\phi(\theta)$ then h(S) is the UMVUE of $\phi(\theta)$.

Proof: Suppose T is another unbiased estimate of $\phi$. According to Rao-Blackwell, T is improved by E(T|S) so if h(S) is not UMVUE then there must exist another function h^*(S) which is unbiased and whose variance is smaller than that of h(S) for some value of $\theta$. But

$$E_\theta(h^*(S)-h(S)) \equiv 0$$

so, in fact h^*(S) = h(S).

Example: In the $N(\mu,\sigma^2)$ example the random variable $(n-1)s^2/\sigma^2$ has a $\chi^2_{n-1}$ distribution. It follows that

$$E\left[\frac{\sqrt{n-1}s}{\sigma}\right] = \frac{\int_0^\inf... ...frac{x}{2}\right)^{(n-1)/2-1} e^{-x/2} dx}{{2\Gamma((n-1)/2)}}$$

Make the substitution y=x/2 and get

$$E(s) = \frac{\sigma}{\sqrt{n-1}}\frac{\sqrt{2}}{\Gamma((n-1)/2)} \int_0^\infty y^{n/2-1} e^{-y} dy$$

Hence

$$E(s) = \sigma\frac{\sqrt{2(n-1)}\Gamma(n/2)}{\sqrt{n-1}\Gamma((n-1)/2)}$$

The UMVUE of $\sigma$ is then

$$s\frac{\sqrt{n-1}\Gamma((n-1)/2)}{\sqrt{2(n-1)}\Gamma(n/2)}$$

by the Lehmann-Scheffé theorem.

Criticism of Unbiasedness

• UMVUE can be inadmissible for squared error loss meaning there is a (biased, of course) estimate whose MSE is smaller for every parameter value. An example is the UMVUE of $\phi=p(1-p)$which is $\hat\phi =n\hat{p}(1-\hat{p})/(n-1)$. The MSE of
  
  $$\tilde{\phi} = \min(\hat\phi,1/4)$$
  
  
  is smaller than that of $\hat\phi$.

• Unbiased estimation may be impossible.

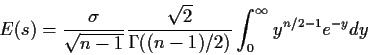
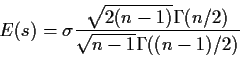
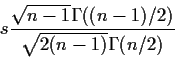
  Binomial(n,p) log odds is $\phi=\log(p/(1-p))$. Since the expectation of any function of the data is a polynomial function of p and since $\phi$ is not a polynomial function of p there is no unbiased estimate of $\phi$

• The UMVUE of $\sigma$ is not the square root of the UMVUE of $\sigma^2$. This method of estimation does not have the parameterization equivariance that maximum likelihood does.

• Unbiasedness is irrelevant (unless you average together many estimators). The property is an average over possible values of the estimate in which positive errors are allowed to cancel negative errors. An exception to this criticism is that if you plan to average a number of estimators to get a single estimator then it is a problem if all the estimators have the same bias. In assignment 5 you have the one way layout example in which the mle of the residual variance averages together many biased estimates and so is very badly biased. That assignment shows that the solution is not really to insist on unbiasedness but to consider an alternative to averaging for putting the individual estimates together.

Minimal Sufficiency

In any model $S(X)\equiv X$ is sufficient. In any iid model the vector $X_{(1)}, \ldots, X_{(n)}$ of order statistics is sufficient. In $N(\mu,1)$ model we have 3 sufficient statistics:

1.

$S_1 = (X_1,\ldots,X_n)$.

2.

$S_2 = (X_{(1)}, \ldots, X_{(n)})$.

3.

$S_3 = \bar{X}$.

Notice that I can calculate S₃ from the values of S₁ or S₂but not vice versa and that I can calculate S₂ from S₁ but not vice versa. It turns out that $\bar{X}$ is a minimal sufficient statistic meaning that it is a function of any other sufficient statistic. (You can't collapse the data set any more without losing information about $\mu$.)

Recognize minimal sufficient statistics from $\ell$:

Fact: If you fix some particular $\theta^*$ then the log likelihood ratio function

$$\ell(\theta)-\ell(\theta^*)$$

is minimal sufficient. WARNING: the function is the statistic.

Subtraction of $\ell(\theta^*)$ gets rid of irrelevant constants in $\ell$. In $N(\mu,1)$ example:

$$\ell(\mu) = -n\log(2\pi)/2 - \sum X_i^2/2 + \mu\sum X_i -n\mu^2/2$$

depends on $\sum X_i^2$, not needed for sufficient statistic. Take $\mu^*=0$ and get

$$\ell(\mu) -\ell(\mu^*) = \mu\sum X_i -n\mu^2/2$$

This function of $\mu$ is minimal sufficient. Notice: from $\sum X_i$ can compute this minimal sufficient statistic and vice versa. Thus $\sum X_i$ is also minimal sufficient.

FACT: A complete sufficient statistic is also minimal sufficient.