Postscript version of these notes

STAT 801 Lecture 19

Reading for Today's Lecture:

Goals of Today's Lecture:

• Introduce concepts of Hypothesis Testing

• Define power, level, most powerful.

• State and prove the Neyman Pearson Lemma

Today's notes

Criticism of Unbiasedness

1.

The UMVUE can be inadmissible for squared error loss, meaning that there is a (biased, of course) estimate whose MSE is smaller for every parameter value. An example is the UMVUE of $\phi=p(1-p)$which is $\hat\phi =n\hat{p}(1-\hat{p})/(n-1)$. The MSE of

$$\tilde{\phi} = \min(\hat\phi,1/4)$$

is smaller than that of $\hat\phi$. Another example is provided by estimation of $\sigma^2$ in the $N(\mu,\sigma^2)$ problem; see the homework.

2.

There are examples where unbiased estimation is impossible. The log odds in a Binomial model is $\phi=\log(p/(1-p))$. Since the expectation of any function of the data is a polynomial function of p and since $\phi$ is not a polynomial function of p there is no unbiased estimate of $\phi$

3.

The UMVUE of $\sigma$ is not the square root of the UMVUE of $\sigma^2$. This method of estimation does not have the parameterization equivariance that maximum likelihood does.

4.

Unbiasedness is irrelevant (unless you plan to average together many estimators). The property is an average over possible values of the estimate in which positive errors are allowed to cancel negative errors. An exception to this criticism is that if you plan to average a number of estimators to get a single estimator then it is a problem if all the estimators have the same bias. In assignment 5 you have the one way layout example in which the mle of the residual variance averages together many biased estimates and so is very badly biased. That assignment shows that the solution is not really to insist on unbiasedness but to consider an alternative to averaging for putting the individual estimates together.

Minimal Sufficiency

In any model the statistic $S(X)\equiv X$ is sufficient. In any iid model the vector of order statistics $X_{(1)}, \ldots, X_{(n)}$ is sufficient. In the $N(\mu,1)$ model then we have three possible sufficient statistics:

1.

$S_1 = (X_1,\ldots,X_n)$.

2.

$S_2 = (X_{(1)}, \ldots, X_{(n)})$.

3.

$S_3 = \bar{X}$.

Notice that I can calculate S₃ from the values of S₁ or S₂but not vice versa and that I can calculate S₂ from S₁ but not vice versa. It turns out that $\bar{X}$ is a minimal sufficient statistic meaning that it is a function of any other sufficient statistic. (You can't collapse the data set any more without losing information about $\mu$.)

To recognize minimal sufficient statistics you look at the likelihood function:

Fact: If you fix some particular $\theta^*$ then the log likelihood ratio function

$$\ell(\theta)-\ell(\theta^*)$$

is minimal sufficient. WARNING: the function is the statistic.

The subtraction of $\ell(\theta^*)$ gets rid of those irrelevant constants in the log-likelihood. For instance in the $N(\mu,1)$ example we have

$$\ell(\mu) = -n\log(2\pi)/2 - \sum X_i^2/2 + \mu\sum X_i -n\mu^2/2$$

This depends on $\sum X_i^2$ which is not needed for the sufficient statistic. Take $\mu^*=0$ and get

$$\ell(\mu) -\ell(\mu^*) = \mu\sum X_i -n\mu^2/2$$

This function of $\mu$ is minimal sufficient. Notice that from $\sum X_i$ you can compute this minimal sufficient statistic and vice versa. Thus $\sum X_i$ is also minimal sufficient.

FACT: A complete sufficient statistic is also minimal sufficient.

Hypothesis Testing

Hypothesis testing is a statistical problem where you must choose, on the basis of data X, between two alternatives. We formalize this as the problem of choosing between two hypotheses: $H_o: \theta\in \Theta_0$ or $H_1: \theta\in\Theta_1$ where $\Theta_0$ and $\Theta_1$ are a partition of the model $P_\theta; \theta\in \Theta$. That is $\Theta_0 \cup \Theta_1 = \Theta$ and $\Theta_0 \cap\Theta_1=\empty$.

A rule for making the required choice can be described in two ways:

1.

In terms of the set

$$C=\{X: \mbox{we choose $\Theta_1$ if we observe $X$}\}$$

called the rejection or critical region of the test.

2.

In terms of a function $\phi(x)$ which is equal to 1 for those x for which we choose $\Theta_1$ and 0 for those x for which we choose $\Theta_0$.

For technical reasons which will come up soon I prefer to use the second description. However, each $\phi$ corresponds to a unique rejection region $R_\phi=\{x:\phi(x)=1\}$.

The Neyman Pearson approach to hypothesis testing which we consider first treats the two hypotheses asymmetrically. The hypothesis H_o is referred to as the null hypothesis (because traditionally it has been the hypothesis that some treatment has no effect).

Definition: The power function of a test $\phi$(or the corresponding critical region $R_\phi$) is

$$\pi(\theta) = P_\theta(X\in R_\phi) = E_\theta(\phi(X))$$

We are interested here in optimality theory, that is, the problem of finding the best $\phi$. A good $\phi$ will evidently have $\pi(\theta)$ small for $\theta\in\Theta_0$and large for $theta\in\Theta_1$. There is generally a trade off which can be made in many ways, however.

Simple versus Simple testing

Finding a best test is easiest when the hypotheses are very precise.

Definition: A hypothesis H_i is simple if $\Theta_i$ contains only a single value $\theta_i$.

The simple versus simple testing problem arises when we test $\theta=\theta_0$ against $\theta=\theta_1$ so that $\Theta$has only two points in it. This problem is of importance as a technical tool, not because it is a realistic situation.

Suppose that the model specifies that if $\theta=\theta_0$ then the density of X is f₀(x) and if $\theta=\theta_1$ then the density of X is f₁(x). How should we choose $\phi$? To answer the question we begin by studying the problem of minimizing the total error probability.

We define a Type I error as the error made when $\theta=\theta_0$ but we choose H₁, that is, $X\in R_\phi$. The other kind of error, when $\theta=\theta_1$ but we choose H₀ is called a Type II error. We define the level of a simple versus simple test to be

$$\alpha = P_{\theta_0}(\mbox{We make a Type I error})$$

or

$$\alpha = P_{\theta_0}(X\in R_\phi) = E_{\theta_0}(\phi(X))$$

The other error probability is denoted $\beta$ and defined as

$$\beta= P_{\theta_1}(X\not\in R_\phi) = E_{\theta_1}(1-\phi(X))$$

Suppose we want to minimize $\alpha+\beta$, the total error probability. We want to minimize

$$E_{\theta_0}(\phi(X))+E_{\theta_1}(1-\phi(X)) = \int[ \phi(x) f_0(x) +(1-\phi(x))f_1(x)] dx$$

The problem is to choose, for each x, either the value 0 or the value 1, in such a way as to minimize the integral. But for each x the quantity

$$\phi(x) f_0(x) +(1-\phi(x))f_1(x)$$

can be chosen either to be f₀(x) or f₁(X). To make it small we take $\phi(x) = 1$ if f₁(x)> f₀(x) and $\phi(x) = 0$ if f₁(x) < f₀(x). It makes no difference what we do for those x for which f₁(x)=f₀(x). Notice that we can divide both sides of these inequalities to rephrase the condition in terms of the likelihood ration f₁(x)/f₀(x).

Theorem: For each fixed $\lambda$ the quantity $\lambda\beta+\alpha$ is minimized by any $\phi$ which has

$$\phi(x) =\left\{\begin{array}{ll} 1 & \frac{f_1(x)}{f_0(x)} >... ...bda \\ 0 & \frac{f_1(x)}{f_0(x)} < \lambda \end{array}\right.$$

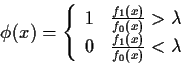
Neyman and Pearson suggested that in practice the two kinds of errors might well have unequal consequences. They suggested that rather than minimize any quantity of the form above you pick the more serious kind of error, label it Type I and require your rule to hold the probability $\alpha$ of a Type I error to be no more than some prespecified level $\alpha_0$. (This value $\alpha_0$is typically 0.05 these days, chiefly for historical reasons.)

The Neyman and Pearson approach is then to minimize beta subject to the constraint $\alpha \le \alpha_0$. Usually this is really equivalent to the constraint $\alpha=\alpha_0$ (because if you use $\alpha<\alpha_0$ you could make R larger and keep $\alpha \le \alpha_0$ but make $\beta$ smaller. For discrete models, however, this may not be possible.

Example: Suppose X is Binomial(n,p) and either p=p₀=1/2 or p=p₁=3/4. If R is any critical region (so R is a subset of $\{0,1,\ldots,n\}$) then

$$P_{1/2}(X\in R) = \frac{k}{2^n}$$

for some integer k. If we want $\alpha_0=0.05$ with say n=5 for example we have to recognize that the possible values of $\alpha$ are 0, 1/32=0.03125, 2/32=0.0625 and so on. For $\alpha_0=0.05$ we must use one of three rejection regions: R₁ which is the empty set, R₂ which is the set x=0 or R₃ which is the set x=5. These three regions have alpha equal to 0, 0.3125 and 0.3125 respectively and $\beta$ equal to 1, 1-(1/4)⁵ and 1-(3/4)⁵ respectively so that R₃ minimizes $\beta$ subject to $\alpha<0.05$. If we raise $\alpha_0$ slightly to 0.0625 then the possible rejection regions are R₁, R₂, R₃ and a fourth region $R_4=R_2\cup R_3$. The first three have the same $\alpha$and $\beta$ as before while R₄ has $\alpha=\alpha_0=0.0625$an $\beta=1-(3/4)^5-(1/4)^5$. Thus R₄ is optimal! The trouble is that this region says if all the trials are failures we should choose p=3/4 rather than p=1/2 even though the latter makes 5 failures much more likely than the former.

The problem in the example is one of discreteness. Here's how we get around the problem. First we expand the set of possible values of $\phi$to include numbers between 0 and 1. Values of $\phi(x)$ between 0 and 1 represent the chance that we choose H₁ given that we observe x; the idea is that we actually toss a (biased) coin to decide! This tactic will show us the kinds of rejection regions which are sensible. In practice we then restrict our attention to levels $\alpha_0$ for which the best $\phi$ is always either 0 or 1. In the binomial example we will insist that the value of $\alpha_0$be either 0 or $P_{\theta_0} ( X\ge 5)$ or $P_{\theta_0} ( X\ge 4)$or ...

Definition: A hypothesis test is a function $\phi(x)$whose values are always in [0,1]. If we observe X=x then we choose H₁ with conditional probability $\phi(X)$. In this case we have

$$\pi(\theta) = E_\theta(\phi(X))$$

$$\alpha = E_0(\phi(X))$$

and

$$\beta = E_1(\phi(X))$$

The Neyman Pearson Lemma

Theorem: In testing f₀ against f₁ the probability $\beta$ of a type II error is minimized, subject to $\alpha \le \alpha_0$by the test function:

$$\phi(x) =\left\{\begin{array}{ll} 1 & \frac{f_1(x)}{f_0(x)} >... ...bda \\ 0 & \frac{f_1(x)}{f_0(x)} < \lambda \end{array}\right.$$

where $\lambda$ is the largest constant such that

$$P_0( \frac{f_1(x)}{f_0(x)} \ge \lambda) \ge \alpha_0$$

and

$$P_0( \frac{f_1(x)}{f_0(x)}\le \lambda) \ge 1-\alpha_0$$

and where $\gamma$ is any number chosen so that

$$E_0(\phi(X)) = P_0( \frac{f_1(x)}{f_0(x)} > \lambda) + \gamma P_0( \frac{f_1(x)}{f_0(x)} =\lambda) = \alpha_0$$

The value of $\gamma$ is unique if $P_0( \frac{f_1(x)}{f_0(x)} = \lambda) > 0$.

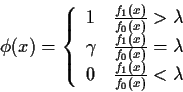
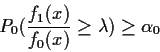
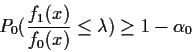
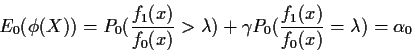
Example: In the Binomial(n,p) with p₀=1/2 and p₁=3/4the ratio f₁/f₀ is

3^x 2^-n

Now if n=5 then this ratio must be one of the numbers 1, 3, 9, 27, 81, 243 divided by 32. Suppose we have $\alpha = 0.05$. The value of $\lambda$ must be one of the possible values of f₁/f₀. If we try $\lambda = 343/32$ then

$$P_0(3^X 2^{-5} \ge 343/32) = P_0(X=5) = 1/32 < 0.05$$

and

$$P_0(3^X 2^{-5} \ge 81/32) = P_0(X \ge 4) = 6/32 > 0.05$$

This means that $\lambda=81/32$. Since

P₀(3^X 2^-5 > 81/32) =P₀( X=5) =1/32

we must solve

$$P_0(X=5) + \gamma P_0(X=4) = 0.05$$

for $\gamma$ and find

$$\gamma = \frac{0.05-1/32}{5/32}= 0.12$$

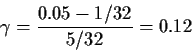
NOTE: No-one ever uses this procedure. Instead the value of $\alpha_0$used in discrete problems is chosen to be a possible value of the rejection probability when $\gamma=0$ (or $\gamma=1$). When the sample size is large you can come very close to any desired $\alpha_0$ with a non-randomized test.

If $\alpha_0=6/32$ then we can either take $\lambda$ to be 343/32 and $\gamma=1$ or $\lambda=81/32$ and $\gamma=0$. However, our definition of $\lambda$ in the theorem makes $\lambda=81/32$ and $\gamma=0$.

When the theorem is used for continuous distributions it can be the case that the cdf of f₁(X)/f₀(X) has a flat spot where it is equal to $1-\alpha_0$. This is the point of the word ``largest'' in the theorem.

Example: If $X_1,\ldots,X_n$ are iid $N(\mu,1)$ and we have $\mu_0=0$ and $\mu_1 >0$ then

$$\frac{f_1(X_1,\ldots,X_n)}{f_0(X_1,\ldots,X_n)} = \exp\{\mu_1 \sum X_i -n\mu_1^2/2 - \mu_0 \sum X_i + n\mu_2^2/2\}$$

which simplifies to

$$\exp\{\mu_1 \sum X_i -n\mu_1^2/2 \}$$

We now have to choose $\lambda$ so that

$$P_0(\exp\{\mu_1 \sum X_i -n\mu_1^2/2 \}> \lambda ) = \alpha_0$$

We can make it equal because in this case f₁(X)/f₀(X) has a continuous distribution. Rewrite the probability as

$$P_0(\sum X_i > [\log(\lambda) +n\mu_1^2/2]/\mu_1) =1-\Phi([\log(\lambda) +n\mu_1^2/2]/[n^{1/2}\mu_1])$$

If $z_\alpha$ is notation for the usual upper $\alpha$ critical point of the normal distribution then we find

$$z_{\alpha_0} = [\log(\lambda) +n\mu_1^2/2]/[n^{1/2}\mu_1]$$

which you can solve to get a formula for $\lambda$ in terms of $z_{\alpha_0}$, n and $\mu_1$.

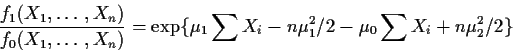
The rejection region looks complicated: reject if a complicated statistic is larger than $\lambda$ which has a complicated formula. But in calculating $\lambda$ we re-expressed the rejection region in terms of

$$\frac{\sum X_i}{\sqrt{n}} > z_{\alpha_0}$$

The key feature is that this rejection region is the same for any $\mu_1 >0$. [WARNING: in the algebra above I used $\mu_1 >0$.] This is why the Neyman Pearson lemma is a lemma!

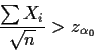
Definition: In the general problem of testing $\Theta_0$ against $\Theta_1$ the level of a test function $\phi$is

$$\alpha = \sup_{\theta\in\Theta_0}E_\theta(\phi(X))$$

The power function is

$$\pi(\theta) = E_\theta(\phi(X))$$

A test $\phi^*$ is a Uniformly Most Powerful level $\alpha_0$test if

1.

$\phi^*$ has level $\alpha \le \alpha_o$

2.

If $\phi$ has level $\alpha \le \alpha_0$ then for every $theta\in\Theta_1$ we have

$$E_\theta(\phi(X)) \le E_\theta(\phi^*(X))$$

Application of the NP lemma: In the $N(\mu,1)$ model consider $\Theta_1=\{\mu>0\}$ and $\Theta_0=\{0\}$ or $\Theta_0=\{\mu \le 0\}$. The UMP level $\alpha_0$ test of $H_0: \mu\in\Theta_0$ against $H_1:\mu\in\Theta_1$ is

$$\phi(X_1,\ldots,X_n) = 1(n^{1/2}\bar{X} > z_{\alpha_0})$$

Proof: For either choice of $\Theta_0$ this test has level $\alpha_0$ because for $\mu\le 0$ we have
$$\begin{align*}P_\mu(n^{1/2}\bar{X} > z_{\alpha_0}) & = P_\mu(n^{1/2}(\bar{X}-\mu... ..._0}-n^{1/2}\mu) \\ & \le P(N(0,1) > z_{\alpha_0}) \\ & = \alpha_0 \end{align*}$$
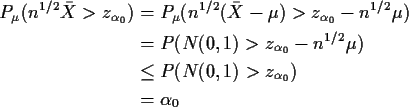
(Notice the use of $\mu\le 0$. The central point is that the critical point is determined by the behaviour on the edge of the null hypothesis.)

Now if $\phi$ is any other level $\alpha_0$ test then we have

$$E_0(\phi(X_1,\ldots,X_n)) \le \alpha_0$$

Fix a $\mu > 0$. According to the NP lemma

$$E_\mu(\phi(X_1,\ldots,X_n)) \le E_\mu(\phi_\mu(X_1,\ldots,X_n))$$

where $\phi_\mu$ rejects if $f_\mu(X_1,\ldots,X_n)/f_0(X_1,\ldots,X_n) > \lambda$ for a suitable $\lambda$. But we just checked that this test had a rejection region of the form

$$n^{1/2}\bar{X} > z_{\alpha_0}$$

which is the rejection region of $\phi^*$. The NP lemma produces the same test for every $\mu > 0$ chosen as an alternative. So we have shown that $\phi_\mu=\phi^*$ for any $\mu > 0$.