Reading for Today's Lecture: Chapter 2
Goals of Today's Lecture:
Today's notes
Last time defined expectation and stated Monotone Convergence Theorem, Dominated Convergence Theorem and Fatou's Lemma. Reviewed elementary definitions of expected value and basic properties of E.
Def'n: The
![]() moment (about the origin) of a real
random variable X is
moment (about the origin) of a real
random variable X is
![]() (provided it exists).
We generally use
(provided it exists).
We generally use
![]() for E(X). The
for E(X). The
![]() central moment is
central moment is
Def'n: For an Rp valued random vector X we define
![]() to be the vector whose
to be the vector whose
![]() entry is E(Xi)(provided all entries exist).
entry is E(Xi)(provided all entries exist).
Def'n: The (
![]() )
variance covariance matrix of X is
)
variance covariance matrix of X is
Moments and probabilities of rare events are closely connected as will
be seen in a number of important probability theorems. Here is one
version of Markov's inequality (one case is Chebyshev's inequality):
![\begin{align*}P(\vert X-\mu\vert \ge t ) &= E[1(\vert X-\mu\vert \ge t)]
\\
&\...
...-\mu\vert \ge t)\right]
\\
& \le \frac{E[\vert X-\mu\vert^r]}{t^r}
\end{align*}](img11.gif)
The intuition is that if moments are small then large deviations from
average are unlikely.
Example moments: If Z is standard normal then
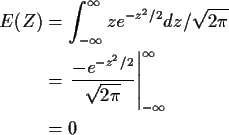
and (integrating by parts)
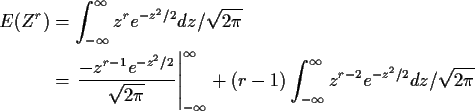
so that
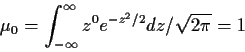
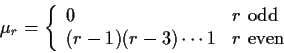
If now
![]() ,
that is,
,
that is,
![]() ,
then
,
then
![]() and
and
Proof: Suppose each Xi is simple:
![]() where the xij are the possible values of Xi. Then
where the xij are the possible values of Xi. Then
![\begin{align*}E(X_1\cdots X_p) & = \sum_{j_1\ldots j_p} x_{1j_1}\cdots x_{pj_p} ...
...ft[\sum_{j_p} x_{pj_p} P(X_p = x_{pj_p})\right]
\\
&= \prod E(X_i)
\end{align*}](img30.gif)
For general Xi>0 we create a sequence of simple approximations
by rounding Xi down to the nearest multiple of 2-n (to
a maximum of n) and applying the case just done and the monotone
convergence theorem. The general case uses the fact that
we can write each Xi as the difference of its positive and negative
parts:
Def'n: The moment generating function of a real valued X is
Def'n: The moment generating function of ![]() is
is
The mgf has the following formal connection to moments:
![\begin{align*}M_X(t) & = \sum_{k=0}^\infty E[(tX)^k]/k!
\\
= \sum_{k=0}^\infty \mu_k^\prime t^k/k!
\end{align*}](img34.gif)
It is thus sometimes possible to find the power series expansion of
MX and read off the moments of X from the coefficients of the
powers tk/k!.
The proof, and many other facts about mgfs, rely on techniques of complex variables.
If
![]() are independent and
are independent and
![]() then
the moment generating function of Y is the product of those
of the individual Xi:
then
the moment generating function of Y is the product of those
of the individual Xi:
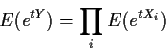
However this formula makes the power series expansion of MY not
a particularly nice function of the expansions of the individual MXi.
In fact this is related to the following observation. The first 3 moments
(meaning ![]() ,
,
![]() and
and ![]() )
of Y are just the sums of those
of the Xi but this doesn't work for the fourth or higher moment.
)
of Y are just the sums of those
of the Xi but this doesn't work for the fourth or higher moment.
![\begin{align*}E(Y) =& \sum E(X_i)
\\
{\rm Var}(Y) =& \sum {\rm Var}(X_i)
\\
E[(Y-E(Y))^3] =& \sum E[(X_i-E(X_i))^3]
\end{align*}](img44.gif)
but
![\begin{align*}E[(Y-E(Y))^4] =& \sum \{E[(X_i-E(X_i))^4] -E^2[(X_i-E(X_i))^2]\}
\\
& + \left\{\sum E[(X_i-E(X_i))^2]\right\}^2
\end{align*}](img45.gif)
It is possible, however, to replace the moments by other objects called
cumulants which do add up properly. The way to define them relies
on the observation that the log of the mgf of Y is the sum of the logs
of the mgfs of the Xi. We define the cumulant generating function of a
variable X by
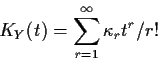
To see the relation between cumulants and moments proceed as follows:
the cumulant generating function is
![]()
To compute the power series expansion we think of the quantity in
![]() as x and expand
as x and expand
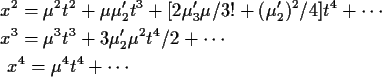
![\begin{multline*}K(t) = \mu t \\
+ [\mu_2^\prime -\mu^2]t^2/2 \\
+ [\mu_3^\pri...
...(\mu_2^\prime)^2 + 12
\mu_2^\prime \mu^2 -6\mu^4]t^4/4! + \cdots
\end{multline*}](img56.gif)
![\begin{align*}\kappa_1 &= \mu
\\
\kappa_2 &= \mu_2^\prime -\mu^2=\sigma^2
\\
\...
...ime)^2 + 12
\mu_2^\prime \mu^2 -6\mu^4
\\ &= E[(X-\mu)^4]-3\sigma^4
\end{align*}](img57.gif)
Check the book by Kendall and Stuart (or the new version called Kendall's Theory of Statistics by Stuart and Ord) for formulas for larger orders r.
Example: If
![]() are independent and Xi has a
are independent and Xi has a
![]() distribution
then
distribution
then
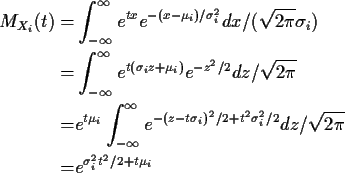
This makes the cumulant generating function
Example: I am having you derive the moment and cumulant generating function
and all the moments of a Gamma rv. Suppose that
![]() are independent
N(0,1) rvs. Then we have defined
are independent
N(0,1) rvs. Then we have defined
![]() to have a
to have a ![]() distribution. It is easy to check S1=Z12 has density
distribution. It is easy to check S1=Z12 has density
Example: The Cauchy density is
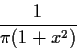
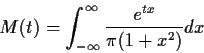
This observation has led to the development of a substitute for the mgf which is defined for every distribution, namely, the characteristic function.
Definition: The characteristic function of a real rv X is
Aside on complex arithmetic.
The complex numbers are the things you get if you add
![]() to the
real numbers and require that all the usual rules of algebra work. In particular
if i and any real numbers a and b are to be complex numbers then so must
be a+bi. If we multiply a complex number a+bi with a and b real by
another such number, say c+di then the usual rules of arithmetic (associative,
commutative and distributive laws) require
to the
real numbers and require that all the usual rules of algebra work. In particular
if i and any real numbers a and b are to be complex numbers then so must
be a+bi. If we multiply a complex number a+bi with a and b real by
another such number, say c+di then the usual rules of arithmetic (associative,
commutative and distributive laws) require
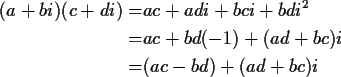
so this is precisely how we define multiplication.
Addition is simply
(again by following the usual rules)
Now look at transcendental functions. For real x we know
![]() so
our insistence on the usual rules working means
so
our insistence on the usual rules working means
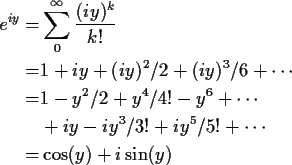
Now every point in the plane can be written in polar co-ordinates as
![]() and comparing this with our formula for the
exponential we see we can write
and comparing this with our formula for the
exponential we see we can write
We will need from time to time a couple of other definitions:
Definition: The modulus of the complex number x+iy is
Definition: The complex conjugate of x+iy is
![]() .
.
Notes on calculus with complex variables. Essentially the usual rules apply so,
for example,
End of Aside
Since