Reading for Today's Lecture:
Goals of Today's Lecture:
Review of end of last time
Proof: Reduces to ![]() and
and ![]() .
.
Step 1: Define
![\begin{align*}f_Y(y) =& (2\pi)^{-n/2} \exp[-y^t\Sigma^{-1}y/2]/\vert\det M\vert
...
...^{-(n-1)/2}\exp[-{\bf y}_2^t Q^{-1} {\bf y}_2/2]}{\vert\det M\vert}
\end{align*}](img11.gif)
Notice ftn of y1 times
ftn of
![]() .
Thus
.
Thus
![]() is independent of
is independent of
![]() .
Since sZ2 is a function of
.
Since sZ2 is a function of
![]() we see that
we see that
![]() and
sZ2 are independent (remember that
and
sZ2 are independent (remember that
![]() ).
).
Also: density of Y1 is a multiple of the function of y1 in
the factorization above. But this is the standard normal
density so
![]() .
.
First 2 parts of theorem done. Third part is homework exercise
but I will outline the derivation of the ![]() density.
density.
Suppose
![]() are independent N(0,1). Define
are independent N(0,1). Define
![]() distribution to be that of
distribution to be that of
![]() .
Define angles
.
Define angles
![]() by
by
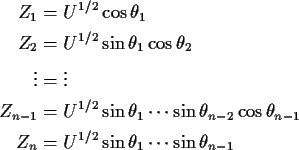
(Spherical co-ordinates in n dimensions. The ![]() values run
from 0 to
values run
from 0 to ![]() except for the last
except for the last ![]() whose values run from 0 to
whose values run from 0 to ![]() .)
Derivative formulas:
.)
Derivative formulas:
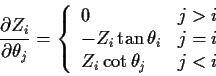
![\begin{displaymath}\left[\begin{array}{ccc}
\frac{
\cos\theta_1
}{
2R}
&
-R \sin...
...1\sin\theta_2
&
R \sin\theta_1\cos\theta_2
\end{array}\right]
\end{displaymath}](img29.gif)
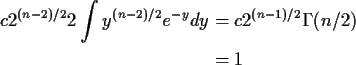
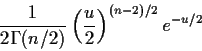
Fourth part of theorem is consequence of
first 3 parts of the theorem and definition of ![]() distribution:
distribution:
![]() if it has same distribution
as
if it has same distribution
as
Derive density of T in this definition:
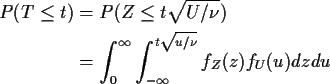
Differentiate wrt t by
differentiating inner integral:
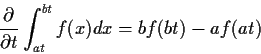
![\begin{align*}\frac{d}{dt} P(T \le t) =&
\int_0^\infty f_U(u) \sqrt{u/\nu}
\\
& \times \frac{\exp[-t^2u/(2\nu)]}{\sqrt{2\pi}} du
\, .
\end{align*}](img50.gif)
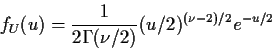
![\begin{align*}f_T(t) = & \int_0^\infty \frac{1}{2\sqrt{\pi\nu}\Gamma(\nu/2)}
\\
&\times (u/2)^{(\nu-1)/2} \exp[-u(1+t^2/\nu)/2] du
\end{align*}](img52.gif)
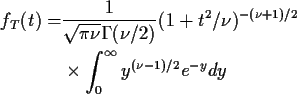
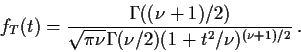
Two elementary definitions of expected values:
Def'n If X has density f then
Def'n: If X has discrete density f then
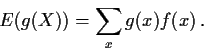
If Y=g(X) for a smooth g
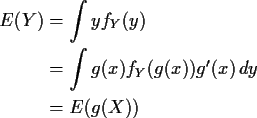
by the change of variables formula for integration. This is good
because otherwise we might have two different values for E(eX).
In general, there are random variables which are neither absolutely continuous nor discrete. Here's how probabilists define E in general.
Def'n: RV X is simple if we can write
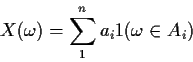
Def'n: For a simple rv X define
For positive random variables which are not simple we extend our definition by approximation:
Def'n: If ![]() then
then
Def'n: We call X integrable if
Facts: E is a linear, monotone, positive operator:
Major technical theorems:
Monotone Convergence: If
![]() and
and
![]() (which has to exist) then
(which has to exist) then
Dominated Convergence: If
![]() and
and ![]() rv X such that
rv X such that ![]() (technical
details of this convergence later in the course) and
a random variable Y such that
(technical
details of this convergence later in the course) and
a random variable Y such that ![]() with
with
![]() then
then
Fatou's Lemma: If ![]() then
then
Theorem: With this definition of E if X has density
f(x) (even in Rp say) and Y=g(X) then
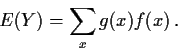
Works, e.g., even if X has a density but Y doesn't.
Def'n: The
![]() moment (about the origin) of a real
rv X is
moment (about the origin) of a real
rv X is
![]() (provided it exists).
We generally use
(provided it exists).
We generally use
![]() for E(X). The
for E(X). The
![]() central moment is
central moment is
Def'n: For an Rp valued random vector X we define
![]() to be the vector whose
to be the vector whose
![]() entry is E(Xi)(provided all entries exist).
entry is E(Xi)(provided all entries exist).
Def'n: The (
![]() )
variance covariance matrix of X is
)
variance covariance matrix of X is
Moments and probabilities of rare events are closely connected as will
be seen in a number of important probability theorems. Here is one
version of Markov's inequality (one case is Chebyshev's inequality):
![\begin{align*}P(\vert X-\mu\vert \ge t ) &= E[1(\vert X-\mu\vert \ge t)]
\\
&\...
...-\mu\vert \ge t)\right]
\\
& \le \frac{E[\vert X-\mu\vert^r]}{t^r}
\end{align*}](img94.gif)
The intuition is that if moments are small then large deviations from
average are unlikely.
Example moments: If Z is standard normal then
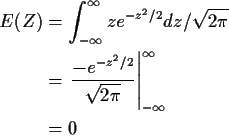
and (integrating by parts)
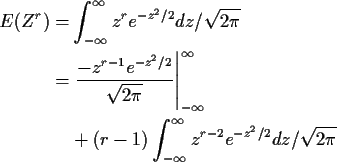
so that
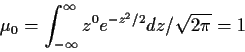
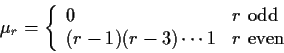
If now
![]() ,
that is,
,
that is,
![]() ,
then
,
then
![]() and
and
Theorem: If
![]() are independent and each Xi is
integrable then
are independent and each Xi is
integrable then
![]() is integrable and
is integrable and
Proof: Suppose each Xi is simple:
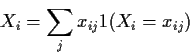
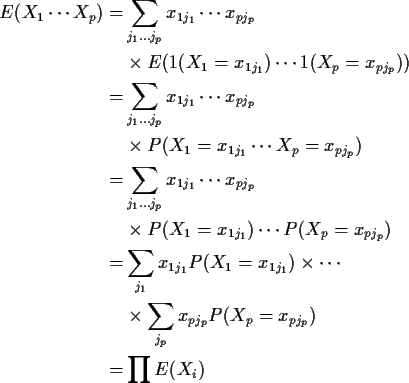
Def'n: The moment generating function of a real valued X is
Def'n: The moment generating function of ![]() is
is
Formal connection to moments:
![\begin{align*}M_X(t) & = \sum_{k=0}^\infty E[(tX)^k]/k!
\\
= \sum_{k=0}^\infty \mu_k^\prime t^k/k!
\end{align*}](img115.gif)
Sometimes can find power series expansion of
MX and read off the moments of X from the coefficients of
tk/k!.
Theorem: If M is finite for all
![]() for some
for some
![]() then
then
The proof, and many other facts about mgfs, rely on techniques of complex variables.