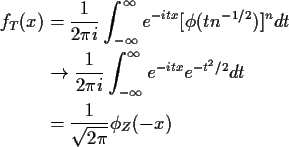Postscript version of this file
STAT 801 Lecture 6
Reading for Today's Lecture:
Goals of Today's Lecture:
- Characteristic Functions
- Review of complex arithmetic
- Inversion formulas
Today's notes
Last time defined moments, moment generating functions, cumulants and
cumulant generating functions. We established the following relations
between moments and cumulants:
![\begin{align*}\kappa_1(X) & = E(X)
\\
\kappa_2(X) & = {\rm Var}(X)
\\
\kappa_3...
...E[(X-E(X))^3]
\\
\kappa_4(X) & = E[(X-E(X))^4] - 3[{\rm Var}(X)]^2
\end{align*}](img2.gif)
Example: I am having you derive
the moment and cumulant generating function
and all the moments of a Gamma rv. Suppose that
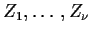 are independent
N(0,1) rvs. Then we have defined
are independent
N(0,1) rvs. Then we have defined
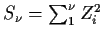 to have a
to have a 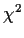 distribution. It is easy to check S1=Z12 has density
distribution. It is easy to check S1=Z12 has density
and then the mgf of S1 is
(1-2t)-1/2
It follows that
you will show in homework that this is the mgf of
a Gamma rv. This shows that the
rv. This shows that the
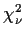 distribution has
the Gamma
distribution has
the Gamma density which is
density which is
Example: The Cauchy density is
the corresponding moment generating function is
which is 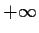 except for t=0 where we get 1.
This mgf is exactly the mgf of every t distribution
so it is not much use for distinguishing such distributions.
The problem is that these distributions do not have infinitely
many finite moments.
except for t=0 where we get 1.
This mgf is exactly the mgf of every t distribution
so it is not much use for distinguishing such distributions.
The problem is that these distributions do not have infinitely
many finite moments.
This observation has led to the development of a substitute for the mgf
which is defined for every distribution, namely, the characteristic function.
Characteristic Functions
Definition: The characteristic function of a real rv X is
where
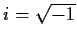 is the imaginary unit.
is the imaginary unit.
Aside on complex arithmetic.
The complex numbers are the things you get if you add
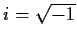 to the
real numbers and require that all the usual rules of algebra work. In particular
if i and any real numbers a and b are to be complex numbers then so must
be a+bi. If we multiply a complex number a+bi with a and b real by
another such number, say c+di then the usual rules of arithmetic (associative,
commutative and distributive laws) require
to the
real numbers and require that all the usual rules of algebra work. In particular
if i and any real numbers a and b are to be complex numbers then so must
be a+bi. If we multiply a complex number a+bi with a and b real by
another such number, say c+di then the usual rules of arithmetic (associative,
commutative and distributive laws) require
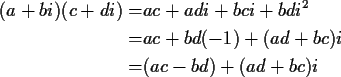
so this is precisely how we define multiplication.
Addition is simply
(again by following the usual rules)
(a+bi)+(c+di) = (a+b)+(c+d)i
Notice that the usual rules of arithmetic then don't require any more numbers
than things of the form
x+yi
where x and y are real. We can identify a single such number x+yi with the
corresponding point (x,y) in the plane. It often helps to picture the complex numbers
as forming a plane.
Now look at transcendental functions. For real x we know
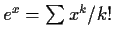 so
our insistence on the usual rules working means
so
our insistence on the usual rules working means
ex+iy = ex eiy
and we need to know how to compute eiy. Remember in what follows that
i2=-1 so i3=-i, i4=1 i5=i1=i and so on. Then

We can thus write
Now every point in the plane can be written in polar co-ordinates as
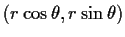 and comparing this with our formula for the
exponential we see we can write
and comparing this with our formula for the
exponential we see we can write
for an angle
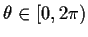 .
.
We will need from time to time a couple of other definitions:
Def'n: The modulus of the complex number x+iy is
Definition: The complex conjugate of x+iy is
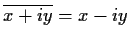 .
.
Notes on calculus with complex variables. Essentially the usual rules apply so,
for example,
We will (mostly) be doing only integrals over the
real line; the theory of integrals along paths in
the complex plane is a very important part of mathematics, however.
End of Aside
Since
we find that
Since the trigonometric functions are bounded by 1 the expected values must
be finite for all t and this is precisely the reason for using
characteristic rather than moment generating functions in probability
theory courses.
Theorem 1
For any two real rvs
X and
Y the following are
equivalent:
- 1.
- X and Y have the same distribution, that is, for any (Borel)
set A we have
- 2.
-
FX(t) = FY(t) for all t.
- 3.
-
 for all real t.
for all real t.
Moreover, all of these are implied if there is a positive

such
that for all

Inversion
The previous theorem is a non-constructive characterization. It does
not show us how to get from 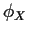 to FX or fX. For cdfs or
densities with reasonable properties, however, there are effective
ways to compute F or f from
to FX or fX. For cdfs or
densities with reasonable properties, however, there are effective
ways to compute F or f from 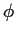 .
In homework I am asking you
to prove the following basic inversion formula:
.
In homework I am asking you
to prove the following basic inversion formula:
If X is a random variable taking only integer values then
for each integer k
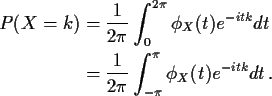
The proof proceeds from the formula
Now suppose that X has a continuous bounded density f. Define
Xn = [nX]/n
where [a] denotes the integer part (rounding down to the next smallest
integer). We have
![\begin{align*}P(k/n \le X < (k+1)/n) = & P([nX]=k)
\\
= & \frac{1}{2\pi} \int_{-\pi}^{\pi} \phi_{[nX]}(t)
\\
&\times e^{-itk} dt \, .
\end{align*}](img37.gif)
Make the substitution t=u/n, and get
![\begin{multline*}n P(k/n \le X < (k+1)/n) =\frac{1}{2\pi}
\\
\times \int_{-n\pi}^{n\pi} \phi_{[nX]}(u/n)e^{iuk/n} du
\end{multline*}](img38.gif)
Now, as
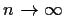 we have
we have
(by the dominated convergence theorem - the dominating random variable
is just the constant 1). The range of integration converges to the whole
real line and if 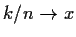 we see that the left hand side converges to
the density f(x) while the right hand side converges to
we see that the left hand side converges to
the density f(x) while the right hand side converges to
which gives the inversion formula
Many other such formulas are available to compute things like
F(b) - F(a)and so on.
All such formulas are sometimes referred to as Fourier inversion formulas;
the characteristic function itself is sometimes called the Fourier
transform of the distribution or cdf or density of X.
Inversion of the Moment Generating Function
The moment generating function and the characteristic function are related
formally by
When MX exists this relationship is not merely formal; the
methods of complex variables mean there is a ``nice'' (analytic)
function which is E(ezX) for any complex
z=x+iy for which MX(x) is finite. All this means
that there is an inversion formula for MX. This formula requires a
complex contour integral. In general if z1 and z2 are two
points in the complex plane and C a path between these two points we
can define the path integral
by the methods of line integration. When it comes to doing algebra with
such integrals the usual theorems of calculus still work. The Fourier
inversion formula was
so replacing 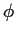 by M we get
by M we get
If we just substitute z=it then we find
where the path C is the imaginary axis. This formula becomes of use by
the methods of complex integration which permit us to replace the path Cby any other path which starts and ends at the same place. It is possible,
in some cases, to choose this path to make it easy to do the integral
approximately; this is what saddlepoint approximations are.
This inversion formula is called the inverse Laplace transform; the mgf is
also called the Laplace transform of the distribution or of the cdf or of
the density.
Applications of Inversion
1): Numerical calculations
Example: Many statistics have a distribution which is approximately that
of
where the Zj are iid N(0,1). In this case
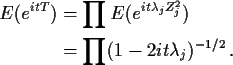
Imhof (Biometrika, 1961) gives a simplification of the Fourier
inversion formula for
FT(x) - FT(0)
which can be evaluated numerically.
2): The central limit theorem (in some versions) can be deduced from
the Fourier inversion formula:
if
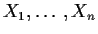 are iid with mean 0 and variance 1 and
are iid with mean 0 and variance 1 and
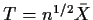 then with
then with 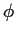 denoting the characteristic function of
a single X we have
denoting the characteristic function of
a single X we have
![\begin{align*}E(e^{itT}) & = E(e^{in^{-1/2} t\sum X_j})
\\
& = \left[\phi(n^{-1...
...sqrt{n}}
+ \frac{t^2\phi^{\prime\prime}(0)}{2n}+ o(n^{-1})\right]^n
\end{align*}](img53.gif)
But now
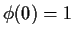 and
and
So
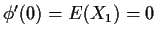 .
Similarly
.
Similarly
so that
It now follows that
![\begin{align*}E(e^{itT}) & \approx [1-t^2/(2n) + o(1/n)]^n
\\
& \to e^{-t^2/2}
\end{align*}](img59.gif)
With care we can then apply the Fourier inversion formula and
get
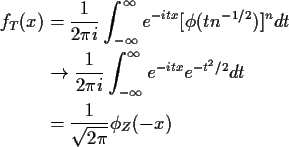
where
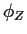 is the characteristic function of a standard normal variable
Z. Doing the integral we find
is the characteristic function of a standard normal variable
Z. Doing the integral we find
so that
which is a standard normal random variable.
This proof of the central limit theorem is not terribly general
since it requires T to have a bounded continuous density. The central
limit theorem itself is a statement about cdfs not densities and is



Richard Lockhart
2000-01-19
![\begin{align*}\kappa_1(X) & = E(X)
\\
\kappa_2(X) & = {\rm Var}(X)
\\
\kappa_3...
...E[(X-E(X))^3]
\\
\kappa_4(X) & = E[(X-E(X))^4] - 3[{\rm Var}(X)]^2
\end{align*}](img2.gif)
![]() are independent
N(0,1) rvs. Then we have defined
are independent
N(0,1) rvs. Then we have defined
![]() to have a
to have a ![]() distribution. It is easy to check S1=Z12 has density
distribution. It is easy to check S1=Z12 has density
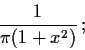
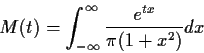
![]() to the
real numbers and require that all the usual rules of algebra work. In particular
if i and any real numbers a and b are to be complex numbers then so must
be a+bi. If we multiply a complex number a+bi with a and b real by
another such number, say c+di then the usual rules of arithmetic (associative,
commutative and distributive laws) require
to the
real numbers and require that all the usual rules of algebra work. In particular
if i and any real numbers a and b are to be complex numbers then so must
be a+bi. If we multiply a complex number a+bi with a and b real by
another such number, say c+di then the usual rules of arithmetic (associative,
commutative and distributive laws) require
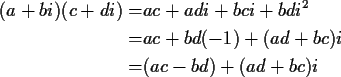
![]() so
our insistence on the usual rules working means
so
our insistence on the usual rules working means

![]() and comparing this with our formula for the
exponential we see we can write
and comparing this with our formula for the
exponential we see we can write
![]() .
.
![]() to FX or fX. For cdfs or
densities with reasonable properties, however, there are effective
ways to compute F or f from
to FX or fX. For cdfs or
densities with reasonable properties, however, there are effective
ways to compute F or f from ![]() .
In homework I am asking you
to prove the following basic inversion formula:
.
In homework I am asking you
to prove the following basic inversion formula:
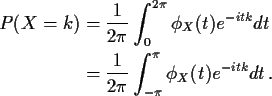
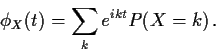
![\begin{align*}P(k/n \le X < (k+1)/n) = & P([nX]=k)
\\
= & \frac{1}{2\pi} \int_{-\pi}^{\pi} \phi_{[nX]}(t)
\\
&\times e^{-itk} dt \, .
\end{align*}](img37.gif)
![\begin{multline*}n P(k/n \le X < (k+1)/n) =\frac{1}{2\pi}
\\
\times \int_{-n\pi}^{n\pi} \phi_{[nX]}(u/n)e^{iuk/n} du
\end{multline*}](img38.gif)
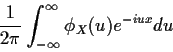
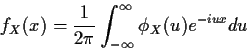
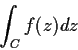


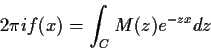
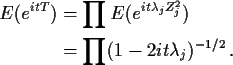
![]() are iid with mean 0 and variance 1 and
are iid with mean 0 and variance 1 and
![]() then with
then with ![]() denoting the characteristic function of
a single X we have
denoting the characteristic function of
a single X we have
![\begin{align*}E(e^{itT}) & = E(e^{in^{-1/2} t\sum X_j})
\\
& = \left[\phi(n^{-1...
...sqrt{n}}
+ \frac{t^2\phi^{\prime\prime}(0)}{2n}+ o(n^{-1})\right]^n
\end{align*}](img53.gif)
![]() and
and
![\begin{align*}E(e^{itT}) & \approx [1-t^2/(2n) + o(1/n)]^n
\\
& \to e^{-t^2/2}
\end{align*}](img59.gif)