Postscript version of these notes

Brownian Motion

For fair random walk = number of heads minus number of tails,

where the are independent and

Notice:

Recall central limit theorem:

Now: rescale time axis so that n steps take 1 time unit and vertical axis so step size is .

We now turn these pictures into a stochastic process:

For we define

Notice:

and

As with t fixed we see . Moreover:

converges to N(0,1) by the central limit theorem. Thus

Another observation: is independent of because the two rvs involve sums of different .

Conclusions.

As the processes converge to a process X with the properties:

1. X(t) has a N(0,t) distribution.
2. X has independent increments: if

   

   then

   

   are independent .

3. The increments are stationary:

   

   regardless of s.

4. X(0)=0.

Def'n: Any process satisfying 1-4 above is a Brownian motion.

Properties of Brownian motion

• Suppose t> s. Then

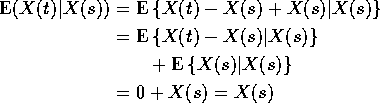
Notice the use of independent increments and of .

• Again if t> s:

  

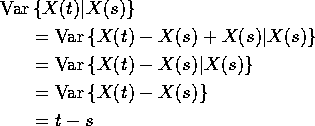
Suppose t< s. Then is a sum of two independent normal variables. Do following calculation:

, and independent. Z=X+Y.

Compute conditional distribution of X given Z:

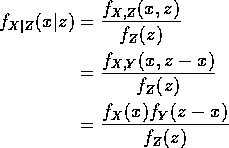
Now Z is where so

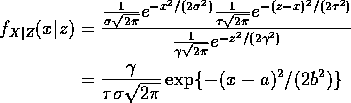
for suitable choices of a and b. To find them compare coefficients of , x and 1.

Coefficient of :

so .

Coefficient of x:

so that

Finally you should check that

to make sure the coefficients of 1 work out as well.

Conclusion: given Z=z the conditional distribution of X is with a and b as above.

Application to Brownian motion:

• For t< s let X be X(t) and Y be X(s)-X(t) so Z=X+Y=X(s). Then , and . Thus

  

  and

  

  SO:

  

  and