Postscript version of these notes

Example: . Then

and the chain is otherwise specivied by and . The matrix is

The backward equations become

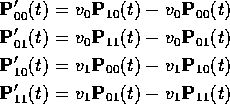
while the forward equations are

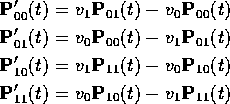
Add first plus third backward equations to get

so

Put t=0 to get . This gives

Plug this back in to the first equation and get

Multiply by and get

which can be integrated to get

Alternative calculation:

can be written as

where

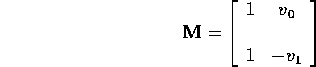
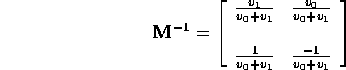
and

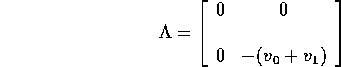
Then

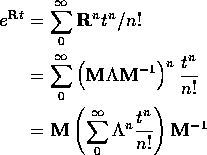
Now

so we get

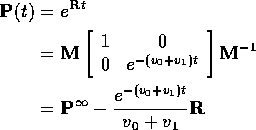
where

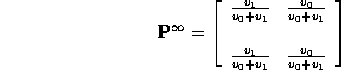
Notice: rows of are a stationary initial distribution. If rows are then

so

Moreover

Fact: is long run fraction of time in state 0.

Fact:

Ergodic Theorem in continuous time.

Birth and Death Processes

Consider a population of X(t) individuals. Suppose in next time interval (t,t+h) probability of population increase of 1 (called a birth) is and probability of decrease of 1 (death) is .

Jargon: X is a birth and death process.

Special cases:

All ; called a pure birth process.

All (0 is absorbing): pure death process.

and is a linear birth and death process.

, : Poisson Process.

and is a linear birth and death process with immigration.

Queuing Theory

Ingredients of Queuing Problem:

1: Queue input process.

2: Number of servers

3: Queue discipline: first come first serve? last in first out? pre-emptive priorities?

4: Service time distribution.

Example: Imagine customers arriving at a facility at times of a Poisson Process N with rate . This is the input process, denoted M (for Markov) in queuing literature.

Single server case:

Service distribution: exponential service times, rate .

Queue discipline: first come first serve.

X(t) = number of customers in line at time t.

X is a Markov process called M/M/1 queue:

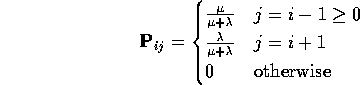
Example: queue:

Customers arrive according to PP rate . Each customer begins service immediately. X(t) is number being served at time t. X is a birth and death process with

and

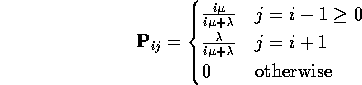
Stationary Initial Distributions

We have seen that a stationary initial distribution is a probability vector solving

Rewrite this as

Interpretation: LHS is rate at which process leaves state j; process is in state j a fraction of time and then makes transition at rate . RHS is total rate of arrival in state j. For each state is fraction of time spent in state i and then the instantaneous rate of transition from i to j.

So equation says:

Rate of departure from j balances rate of arrival to j. This is called balance.

Application to birth and death processes:

Equation is

for and

Notice that this permits the recursion

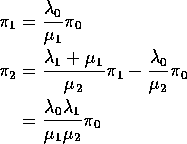
which extends by induction to

Apply to get

This gives the formula announced:

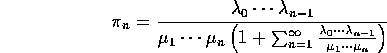
If

then we have defined a probability vector which solves

Since

we see that

so that is constant. Put t=0 to discover that the constant is .