Proof of 4): Fix 
for 
such that
Given N(T)=n we compute the probability of the event
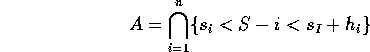
Intersection of A and N(T)=n is ( 
):
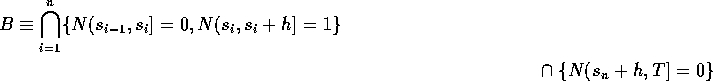
whose probability is
So
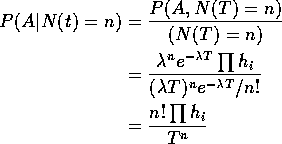
Divide by 
and let all 
go to 0 to
get joint density of 
is
which is the density of order statistics from a Uniform[0,T] sample of size n.
5) Replace the event 
with 
. With
A as before we want
Note that B is independent of 
and that we have
already found the limit
We are left to compute the limit of
The denominator is
so
Finally
Thus
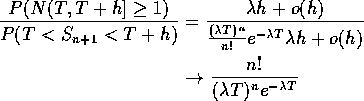
This gives the conditional density of given
as in 4).
Inhomogeneous Poisson Processes
The idea of hazard rate can be used to extend the notion of Poisson
Process. Suppose 
is a function of t. Suppose
N is a counting process such that
and
Then N has independent increments and N(t+s)-N(t) has a Poisson distribution with mean
If we put
then mean of N(t+s)-N(T) is
.
Jargon: 
is the intensity or instaneous intensity
and 
the cumulative intensity.
Can use the model with any non-decreasing right continuous
function, possibly without a derivative. This allows ties.