Postscript version of this file

Convolution: If X and Y independent rvs with densities f and g respectively and Z=X+Y then

Differentiating wrt z we get

This integral is called the convolution of densities f and g.

If iid Exponential then has a Gamma distribution. Density of is

for s> 0.

Proof:

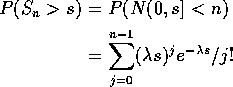
Then

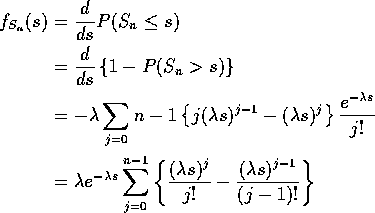
This telescopes to

Properties of Poisson Processes

1)

If and are independent Poisson processes with rates and , respectively the is a Poisson processes with rates .

2)

Suppose N is a Poisson process with rate . Suppose each point is marked with a label, say one of independently of all other occurences. Suppose is the probability that a given point receives label . Let count the points with label i (so that ). Then are independent Poisson processes with rates .

3)

Suppose independent rvs, each uniformly distributed on [0,T]. Suppose M is a Poisson random variable independent of the U's. Let

Then N is a Poisson process on [0,T] with rate .

4)

Suppose N is a Poisson process with rate . Let be the times at which points arrive Given N(T)=n have the same distribution as the order statistics of a sample of size n from the uniform distribution on [0,T].

5)

Given , have the same distribution as the order statistics of a sample of size n from the uniform distribution on [0,T].

Indications of some proofs:

1) independent Poisson processes rates , . Let be the event of 2 or more points in N in the time interval (t,t+h], , the event of exactly one point in N in the time interval (t,t+h].

Let and be the corresponding events for .

Let denote the history of the processes up to time t; we condition on .

Note that

Since

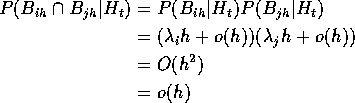
we have checked one of the two infinitesimal conditions for a Poisson process.

Next note

so that

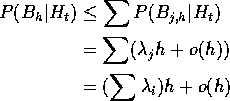
On the other hand let be the event of no points in N in the time interval (t,t+h] and the same for . Then

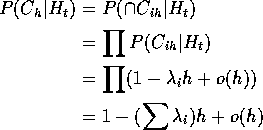
shows

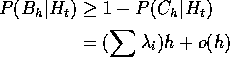
Hence N is a Poisson process with rate .

2) The infinitesimal approach used for 1 can do part of this. See text for rest. Events defined as in 1): The event that there is one point in in (t,t+h] is the event, that there is exactly one point in any of the r processes together with a subset of where there are two or more points in N in (t,t+h] but exactly one is labeled i. Since

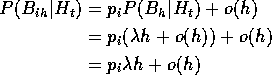
Similarly, is a subset of so

This shows each is Poisson with rate . To get independence requires more work; see the text for the algebraic method which is easier.

3) Fix s< t. Let N(s,t) be the number of points in (s,t]. Given N=n the conditional distribution of N(s,t) is Binomial(n,p) with p=(s-t)/T. So

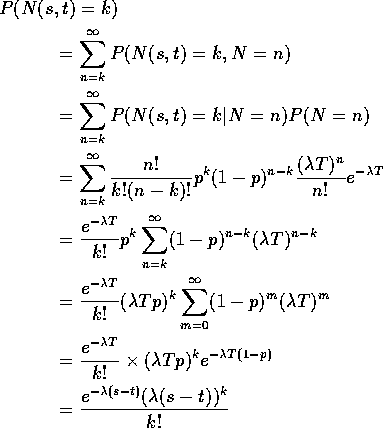
4): Fix for such that

Given N(T)=n we compute the probability of the event

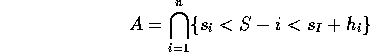
Intersection of A and N(T)=n is ( ):

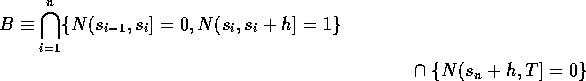
whose probability is

So

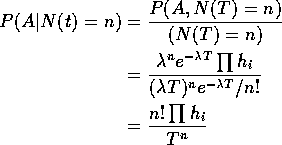
Divide by and let all go to 0 to get joint density of is

which is the density of order statistics from a Uniform[0,T] sample of size n.

5) Replace the event with . With A as before we want

Note that B is independent of and that we have already found the limit

We are left to compute the limit of

The denominator is

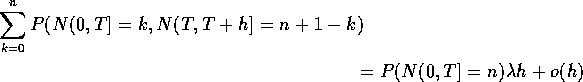
Thus

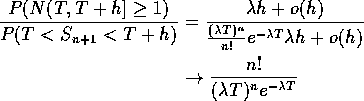
This gives the conditional density of given as in 4).

Inhomogeneous Poisson Processes

The idea of hazard rate can be used to extend the notion of Poisson Process. Suppose is a function of t. Suppose N is a counting process such that

and

Then N has independent increments and N(t+s)-N(t) has a Poisson distribution with mean

If we put

then mean of N(t+s)-N(T) is .

Jargon: is the intensity or instaneous intensity and the cumulative intensity.

Can use the model with any non-decreasing right continuous function, possibly without a derivative. This allows ties.

Continuous Time Markov Chains

Model for population growth: at time t population size is N(t). In next h time units: population goes up 1 or down 1 (or stays same). Larger movements unlikely.

Natural model has probability of birth large when population size large, small when population size small.