Continuous Time Markov Chains
Consider a population of single celled organisms in a stable environment.
Fix short time interval, length h.
Each organism has some probability of dividing to produce two organisms and some other probability of dying.
We might suppose:
Tacit assumptions:
Constants of proportionality do not depend on time: ``stable environment''.
Constants do not depend on organism: organisms are all similar and live in similar environments.
Y(t): total population at time t.
![]() : history of
process up to time t.
: history of
process up to time t.
Condition on event Y(t) =n .
Probability of two or more divisions (more than one division by a single organism or two or more organisms dividing) is o(h).
Probability of both a division and a death or of two or more deaths is o(h).
So probability of exactly 1 division by any one of the n organisms is ![]() .
.
Similarly probability of 1 death is ![]() .
.
We deduce:
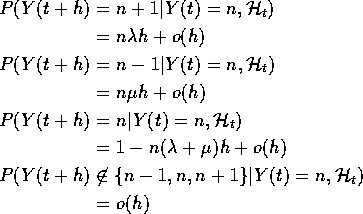
These equations lead to:
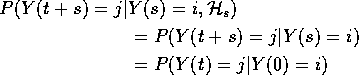
This is the Markov Property.
Definition: A process ![]() taking values in
S, a finite or countable state space is a Markov Chain
if
taking values in
S, a finite or countable state space is a Markov Chain
if
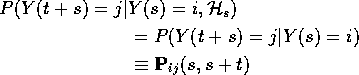
Definition: A Markov chain X has stationary transitions if
![]()
From now on: our chains have stationary transitions.