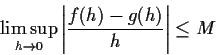Postscript version of this file

STAT 380 Lecture 13

Mean time in transient states

$${\bf P}= \left[\begin{array}{cccc} \frac{1}{2} & \frac{1}{2} ... ... & \frac{1}{4} & \frac{3}{8} & \frac{1}{8} \end{array}\right]$$

States 3 and 4 are transient. Let m_i,j be the expected total number of visits to state j for chain started in i.

For i=1 or i=2 and j=3 or 4:

m_ij = 0

For j=1 or j=2

$$m_{ij} = \infty$$

For $i,j \in \{3,4\}$ first step analysis:
$$\begin{align*}m_{3,3} & = 1+ \frac{1}{4} m_{3,3} + \frac{1}{4} m_{4,3} \\ m_{3,... ...{4,3} \\ m_{4,4} & = 0 + \frac{3}{8} m_{3,4} + \frac{1}{8} m_{4,4} \end{align*}$$

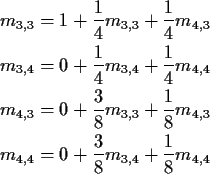
In matrix form
$$\begin{align*}\left[\begin{array}{cc} m_{3,3} &m_{3,4} \\ \\ m_{4,3} &m_{4,4}\e... ...ray}{cc} m_{3,3} &m_{3,4} \\ \\ m_{4,3} &m_{4,4}\end{array}\right] \end{align*}$$

Translate to matrix notation:

$${\bf M} = {\bf I} + {\bf P}_T {\bf M}$$

where $\bf I$ is the identity, $\bf M$ is the matrix of means and ${\bf P}_T$ the part of the transition matrix corresponding to transient states.

Solution is

$${\bf M} = ({\bf I} - {\bf P}_T)^{-1}$$

In our case

$${\bf I} - {\bf P}_T = \left[\begin{array}{rr} \frac{3}{4} &... ...rac{1}{4} \\ \\ -\frac{3}{8} & \frac{7}{8} \end{array}\right]$$

so that

$${\bf M} = \left[\begin{array}{rr} \frac{14}{9} & -\frac{4}{9} \\ \\ -\frac{2}{3} & \frac{4}{3} \end{array}\right]$$

Poisson Processes

Particles arriving over time at a particle detector. Several ways to describe most common model.

Approach 1: numbers of particles arriving in an interval has Poisson distribution, mean proportional to length of interval, numbers in several non-overlapping intervals independent.

For s<t, denote number of arrivals in (s,t] by N(s,t). Model is

1.

N(s,t) has a Poisson $(\lambda(t-s))$ distribution.

2.

For $0 \le s_1 < t_1 \le s_2 < t_2 \cdots \le s_k < t_k$ the variables $N(s_i,t_i);i=1,\ldots,k$ are independent.

Approach 2:

Let $0 < S_1 <S_2 < \cdots$ be the times at which the particles arrive.

Let T_i = S_i-S_i-1 with S₀=0 by convention.

Then $T_1,T_2,\ldots$are independent Exponential random variables with mean $1/\lambda$.

Note $P(T_i > x) =e^{-\lambda x}$ is called survival function of T_i.

Approaches are equivalent. Both are deductions of a model based on local behaviour of process.

Approach 3: Assume:

1.

given all the points in [0,t] the probability of 1 point in the interval (t,t+h] is of the form

$$\lambda h +o(h)$$

2.

given all the points in [0,t] the probability of 2 or more points in interval (t,t+h] is of the form

o(h)

All 3 approaches are equivalent. I show: 3 implies 1, 1 implies 2 and 2 implies 3. First explain o, O.

Notation: given functions f and g we write

f(h) = g(h) +o(h)

provided

$$\lim_{h \to 0} \frac{f(h)-g(h)}{h} = 0$$

[Aside: if there is a constant M such that

$$\limsup_{h \to 0} \left\vert\frac{f(h)-g(h)}{h}\right\vert \le M$$

we say

f(h) = g(h)+O(h)

Notation due to Landau. Another form is

f(h) = g(h)+O(h)

means there is $\delta>0$ and M s.t. for all $\vert h\vert<\delta$

$$\vert f(h)-g(h) \vert\le M h$$

Idea: o(h) is tiny compared to h while O(h) is (very) roughly the same size as h.]