Postscript version of this file

STAT 380 Lecture 12

One Example

Page 229, question 21: runner goes from front or back door, prob 1/2 each. Returns front or back, prob 1/2 each. Has k pairs of shoes, wears pair if any at departure door, leaves at return door. No shoes? Barefoot. Long run fraction of time barefoot?

Solution: Let X_n be number of shoes at front door on day n. Then X_n is a Markov Chain.

Transition probabilities:

k pairs at front door on day n. X_n+1 is k if goes out back door (prob is 1/2) or out front door and back in front door (prob is 1/4). Otherwise X_n+1 is k-1.

0 < j < k pairs at front door on day n. X_n+1 is j+1if out back, in front (prob is 1/4). X_n+1 is j-1 if out front, in back. Otherwise X_n+1 is j.

0 pairs at front door on day n. X_n+1 is 0 if out front door (prob 1/2) or out back door and in back door (prob 1/4) otherwise X_n+1 is 1.

Transition matrix ${\bf P}$:

$$\left[\begin{array}{cccccc} \frac{3}{4} & \frac{1}{4} & 0 & 0... ... 0 & 0 & \cdots & \frac{1}{4} & \frac{3}{4} \end{array}\right]$$

Doubly stochastic: row sums and column sums are 1.

So $\pi_i=1/(k+1)$ for all i is stationary initial distribution.

Solution to problem: 1 day in k+1 no shoes at front door. Half of those go barefoot. Also 1 day in k+1 all shoes at front door; go barefoot half of these days. Overall go barefoot 1/(k+1) of the time.

Gambler's Ruin

Insurance company's reserves fluctuate: sometimes up, sometimes down. Ruin is event they hit 0 (company goes bankrupt). General problem. For given model of fluctuation compute probability of ruin either eventually or in next k time units.

Simplest model: gambling on Red at Casino. Bet $1 at a time. Win $1 with probability p, lose $1 with probability 1-p. Start with k dollars. Quit playing when down to $0 or up to N. Compute

$$P_k = P(\text{reach $N$ before $0$})$$

X_n = fortune after n plays. X₀=k.

Transition matrix:

$${\bf P}= \left[\begin{array}{cccccc} 1 & 0 & 0 & 0 &\cdots &... ...ots & \vdots \\ 0 & 0 & 0 & \cdots & 0 & 1 \end{array}\right]$$

First step analysis:
$$\begin{align*}P_0 & =0 \\ P_i & = (1-p) P_{i-1}+pP_{i+1} \\ P_N & = 1 \end{align*}$$

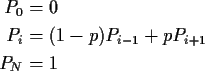
Middle equation is

pP_i +(1-p)P_i = (1-p) P_i-1+pP_i+1

or
$$\begin{align*}P_{i+1}-P_{i} &= \frac{1-p}{p} (P_{i}-P_{i-1}) \\ & = \left( \fra... ...}\right)^{i} (P_1-P_{0}) \\ & = \left( \frac{1-p}{p}\right)^{i}P_1 \end{align*}$$
Sum from i=0 to i=k-1 to get

$$P_k = \sum_{i=0}^{k-1} \left( \frac{1-p}{p}\right)^i P_1$$

or

$$P_k = \frac{1-\{(1-p)/p\}^k}{1-\{(1-p)/p\}} P_1$$

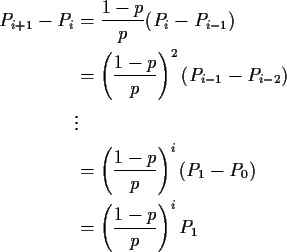
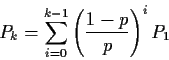
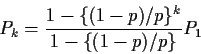
For k=N we get

$$1=\frac{1-\{(1-p)/p\}^N}{1-\{(1-p)/p\}} P_1$$

so that

$$P_k = \frac{1-\{(1-p)/p\}^k}{1-\{(1-p)/p\}^N} P_1$$

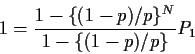
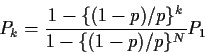
Notice that if p=1/2 our formulas for the sum of the geometric series are wrong. But for p=1/2 we get

P_k=kP₁

so

$$P_k=\frac{k}{N} \, .$$