Postscript version of this file

STAT 380 Lecture 11

Hitting Times

Start irreducible recurrent chain X_n in state i. Let T_j be first n>0 such that X_n=j. Define

$$m_{ij} = {\rm E}(T_j\vert X_0=i)$$

First step analysis:
$$\begin{align*}m_{ij} & = 1\cdot P(X_1=j\vert X_0=i) \\ & \qquad + \sum_{k\neq j... ...um_{k\neq j} P_{ik} m_{kj} \\ & = 1 + \sum_{k\neq j} P_{ik} m_{kj} \end{align*}$$

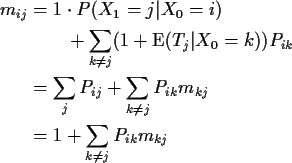
Example

$${\bf P}= \left[\begin{array}{cc} \frac{3}{5} & \frac{2}{5} \\ \\ \frac{1}{5} & \frac{4}{5} \end{array} \right]$$

The equations are
$$\begin{align*}m_{11} & = 1 +\frac{2}{5} m_{21} \\ m_{12} & = 1 +\frac{3}{5} m_{... ...{21} & = 1 +\frac{4}{5} m_{21} \\ m_{22} & = 1 +\frac{1}{5} m_{12} \end{align*}$$
The second and third equations give immediately
$$\begin{align*}m_{12} & = \frac{5}{2} \\ m_{21} & = 5 \end{align*}$$
Then plug in to the others to get
$$\begin{align*}m_{11} & = 3 \\ m_{22} & = \frac{3}{2} \end{align*}$$

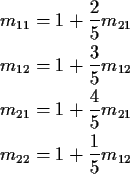
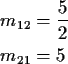
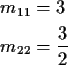
Notice stationary initial distribution is

$$\left(\frac{1}{m_{11}},\frac{1}{m_{22}}\right)$$

Consider fraction of time spent in state j:

$$\frac{1(X_0=j)+\cdots+1(X_n=j)}{n+1}$$

Imagine chain starts in chain i; take expected value.

$$\frac{\sum_{r=1}^n {\bf P}^r_{ij} +1(i=j)}{n+1}$$

If rows of ${\bf P}$ converge to $\pi$ then fraction converges to $\pi_j$; i.e. limiting fraction of time in state j is $\pi_j$.

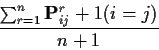
Heuristic: start chain in i. Expect to return to i every m_ii time units. So are in state i about once every m_ii time units; i.e. limiting fraction of time in state iis 1/m_ii.

Conclusion: for an irreducible recurrent finite state space Markov chain

$$\pi_i = \frac{1}{m_{ii}} \, .$$

Infinite State Spaces

Previous conclusion is still right if there is a stationary initial distribution.

Example: $X_n = \text{Heads}-\text{Tails}$ after n tosses of fair coin. Equations are
$$\begin{align*}m_{0,0} & = 1 + \frac{1}{2}m_{1,0}+\frac{1}{2} m_{-1,0} \\ m_{1,0} & = 1 + \frac{1}{2} m_{2,0} \end{align*}$$
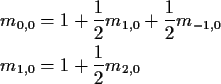
and many more.

Some observations:

You have to go through 1 to get to 0 from 2 so

m_2,0=m_2,1+m_1,0

Symmetry (switching H and T):

m_1,0=m_-1,0

The transition probabilities are homogeneous:

m_2,1=m_1,0

Conclusion:

$$\begin{align*}m_{0,0} & = 1 + m_{1,0} \\ & = 1+ 1 + \frac{1}{2} m_{2,0} \\ & = 2 + m_{1,0} \end{align*}$$
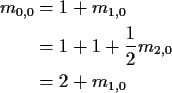
Notice that there are no finite solutions!

Summary of the situation:

Every state is recurrent.

All the expected hitting times m_ij are infinite.

All entries ${\bf P}^n_{ij}$ converge to 0.

Jargon: The states in this chain are null recurrent.