STAT 330 Lecture 27

Reading for Today's Lecture: 11.1, 11.2.

Goals of Today's Lecture:

• Complete the discussion of F tests in two way factorial designs.
• Discuss confidence intervals for contrasts.
• Introduce the ANOVA table for a two way layout without replications.
• Review a SAS example.

Today's notes

Two way layout: the ANOVA table

Sum of Mean

Source df Squares Square F P

I-1 SS/df

J-1 SS/df

(I-1)(J-1) SS/df

IJ(K-1) SS/df

Total n-1

There are 3 F-statistics for each of which P values come from F tables with degrees of freedom which are recorded in the degrees of freedom column:

• , used to test the hypothesis of no interactions.
• , used, if the previous null is accepted to test the hypothesis that the main effects of FACTOR 1 are 0.
• , used, if the first hypothesis is accepted to test the hypothesis that the main effects of FACTOR 2 are 0.

Example: the variable X is plaster hardness. The factors are SAND content (with levels 0, 15 and 30%) and FIBRE content (with levels 0, 25 and 50%). We have 2 replicates so I=3, J=3 and K=2.

SAS analysis

The data consist of casting hardnesses for 18 samples prepared under 3 levels of sand added and 3 levels of carbon fibre added. See Q 15 in Chapter 11. I use proc anova to test the hypotheses of no effect of either sand content or fibre content after first testing for interactions.

I ran the following SAS code:

 options pagesize=60 linesize=80;
  data plaster;
  infile 'plaster.dat';
  input sand fibre hardness strength;
  proc anova  data=plaster;
   class sand fibre;
   model hardness = sand|fibre;
   means sand fibre / tukey cldiff ;
  run;

The line labelled model says that I am interested in the effects of sand, fibre and interactions between the two. The line class sand fibre is required so that SAS knows which variables define the levels of the factors.

The output from proc anova begins with a print out of information about the variables SAND and FIBRE: how many levels there are and what the levels are called.

                                 The SAS System                                1
                                                14:05 Tuesday, November 14, 1995

                         Analysis of Variance Procedure
                            Class Level Information

                           Class    Levels    Values

                           SAND          3    0 15 30

                           FIBRE         3    0 25 50


                    Number of observations in data set = 18

Next SAS produces the ANOVA table. You should notice that it first prints out a table with three lines: MODEL, ERROR and TOTAL. The line labelled MODEL is the sum of the three lines "Factor 1", "Factor 2", and "Interactions" in the table I have shown above.

                                 The SAS System                                2
                                                14:05 Tuesday, November 14, 1995

                         Analysis of Variance Procedure

Dependent Variable: HARDNESS
                                     Sum of            Mean
Source                  DF          Squares          Square   F Value     Pr > F

Model                    8     202.77777778     25.34722222      3.10     0.0557

Error                    9      73.50000000      8.16666667

Corrected Total         17     276.27777778

Next it prints some summary statistics, including the Root MSE which is in this case.

                  R-Square             C.V.        Root MSE        HARDNESS Mean

                  0.733963         4.105290       2.8577380            69.611111

Finally it breaks the model line down into the three lines in my table above. You can check that these lines add up to the model line above.

Source                  DF         Anova SS     Mean Square   F Value     Pr > F

SAND                     2     106.77777778     53.38888889      6.54     0.0176
FIBRE                    2      87.11111111     43.55555556      5.33     0.0297
SAND*FIBRE               4       8.88888889      2.22222222      0.27     0.8887

The conclusions are that both sand and fibre have an effect on hardness but that there is little evidence of an interaction between the two factors. (These are based on the column of P values, 0.0176, 0.0297 and 0.8887.)

Finally here are the results of the line which asked for Tukey confidence intervals.

                                 The SAS System                                3
                                                14:05 Tuesday, November 14, 1995

                         Analysis of Variance Procedure

          Tukey's Studentized Range (HSD) Test for variable: HARDNESS

          NOTE: This test controls the type I experimentwise error rate.

              Alpha= 0.05  Confidence= 0.95  df= 9  MSE= 8.166667
                   Critical Value of Studentized Range= 3.948
                     Minimum Significant Difference= 4.6066

       Comparisons significant at the 0.05 level are indicated by '***'.

                            Simultaneous            Simultaneous
                                Lower    Difference     Upper
                 SAND        Confidence    Between   Confidence
              Comparison        Limit       Means       Limit

             30   - 15         -2.773       1.833       6.440
             30   - 0           1.227       5.833      10.440   ***

             15   - 30         -6.440      -1.833       2.773
             15   - 0          -0.607       4.000       8.607

             0    - 30        -10.440      -5.833      -1.227   ***
             0    - 15         -8.607      -4.000       0.607


                                 The SAS System                                4
                                                14:05 Tuesday, November 14, 1995

                         Analysis of Variance Procedure

          Tukey's Studentized Range (HSD) Test for variable: HARDNESS

          NOTE: This test controls the type I experimentwise error rate.

              Alpha= 0.05  Confidence= 0.95  df= 9  MSE= 8.166667
                   Critical Value of Studentized Range= 3.948
                     Minimum Significant Difference= 4.6066

       Comparisons significant at the 0.05 level are indicated by '***'.

                            Simultaneous            Simultaneous
                                Lower    Difference     Upper
                FIBRE        Confidence    Between   Confidence
              Comparison        Limit       Means       Limit

             50   - 25         -4.607       0.000       4.607
             50   - 0           0.060       4.667       9.273   ***

             25   - 50         -4.607       0.000       4.607
             25   - 0           0.060       4.667       9.273   ***

             0    - 50         -9.273      -4.667      -0.060   ***
             0    - 25         -9.273      -4.667      -0.060   ***

The Tukey procedures show a clear difference between the 0% fibre and the other two levels with 0 FIBRE clearly lowering hardness. There is no clear difference between the 25% and 50% FIBRE levels in terms of effect on hardness. The high level of sand clearly differs from the low level but the intermediate level is not clearly distinguished from the other two.

Thus, the SAS output shows that the ANOVA table is as follows:

Sum of Mean

Source df Squares Square F P

2 106.8 53.4 6.54 0.018

2 87.1 43.6 5.33 0.030

4 8.89 2.22 0.27 0.89

9 73.5 8.17

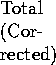17 276.28

Conclusions:

1. : no interactions is accepted.
2. There are significant SAND effects.
3. There are significant FIBRE effects.

NEXT: multiple comparisons and Tukey confidence intervals.

0 15 30

In other words the level 0 differs from the level 30 but we cannot distinguish clearly 15 from either 30 or 0% SAND.

Two way layouts without replicates (K=1)

When K=1 we do not have enough data to estimate the s. So we simplify the model to

Notice that we have droped the s and the subscript k. The estimates for the parameters are now

and so on; these are the same as for K>1. The fitted residuals are

The ANOVA table simplifies to

Sum of Mean

Source df Squares Square F P

I-1 SS/df

J-1 SS/df

(I-1)(J-1) SS/df

Total n-1

Notice the match between the degrees of freedom for Error and the degrees of freedom for interactions when there were replicates. We could actually fit a model with interactions even though K=1 but we would find that the error sum of squares was 0. In fact the line here labelled Error would there belabelled Interaction.

This ANOVA table can be used to test the hypotheses of no main effects for Factor 1 and no main effects for Factor 2, that is, the hypotheses and .