STAT 330 Lecture 26

Reading for Today's Lecture: 11.1, 11.2.

Goals of Today's Lecture:

• Describe the least squares estimates in the two way layout.
• Introduce the ANOVA table for a two way layout with replications.
• Review a SAS example.

Today's notes

Two way layout

Data

Model equation

where the are independent random variables with mean 0 and variance (usually with distributions.

We decompose as

which has many possible solutions for , , and . We choose

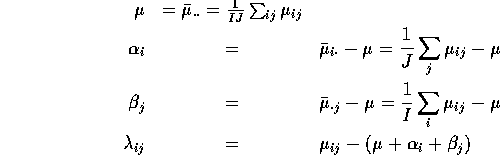
Remarks:

1. 's are called interactions.
2. If K=1 we drop the subscript k and assume that the are all 0.

Two numerical examples:

Table of hypothetical means:

Treatment Control

Men 120 130 1

Women 105 115 2

1 2

, and so on.

According to our definitions:

and

Similarly we find , and .

Now consider instead the table

Treatment Control

Men 120 130 1

Women 115 105 2

1 2

for which , , and . Note that the main effect of treatment is 0; averaged over men and women the drug does nothing. However, the drug actually works for men, lowering BP by 10, while it is a total failure for women, raising BP by 10. In the presence of interactions the main effect of a factor is not a very meaningful quantity.

Analysis of the data when K > 1

1. Estimation:

   

2. Hypothesis testing: we have the following hypotheses to test:
   1. No interactions: for all i,j.
   2. No effect of factor 1: for all i.
   3. No effect of factor 2: for all j.

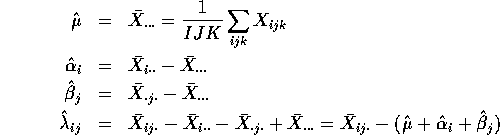
Note: Hypotheses (b) and (c) are tested only if in (a) is accepted. The logic of this is that if a drug affects men and women differently (that is sex and treatment have an interaction) then the drug certainly has some effect and the average effect is of no real interest.

Tests are based on an ANOVA table

Sum of Mean

Source df Squares Square F P

I-1 SS/df

J-1 SS/df

(I-1)(J-1) SS/df

IJ(K-1) SS/df

Total n-1

Remark: many of the formulas simplify. For example

Theory:

If all then

If then

and so on.

All of the sums of squares above the line in the table are independent.

There are 3 F-statistics for each of which P values come from F tables with degrees of freedom which are recorded in the degrees of freedom column:

• 
• 
• 

Example: the variable X is plaster hardness. The factors are SAND content (with levels 0, 15 and 30%) and FIBRE content (with levels 0, 25 and 50%). We have 2 replicates so I=3, J=3 and K=2. SAS output shows that the ANOVA table is as follows:

Sum of Mean

Source df Squares Square F P

2 106.8 53.4 6.54 0.018

2 87.1 43.6 5.33 0.030

4 8.89 2.22 0.27 0.89

9 73.5 8.17

17 276.28

Conclusions:

1. : no interactions is accepted.
2. There are significant SAND effects.
3. There are significant FIBRE effects.

NEXT: multiple comparisons and Tukey confidence intervals.

0 15 30

In other words the level 0 differs from the level 30 but we cannot distinguish clearly 15 from either 30 or 0% SAND.