STAT 330 Lecture 18

Reading for Today's Lecture: 9.5, 10.1.

Goals of Today's Lecture:

• Do example of F test for equality of 2 variances.
• Introduce the I sample problem.

Today's notes

We will test the hypothesis in 2 independent samples , using a variance ratio

and get P-values from .

Example: for Michelson data n=m=20 and

In F tables we find

and

so that P < 0.01 for a one sided test. In fact, using SPlus I get P=0.003 one-sided and P=0.006 for a two sided test. Conclusion: The SD of the measurement error has clearly changed from the first 20 to the last 20 measurements.

Next topic: Use same style of test to test

for I>2. This is the so-called ``I sample problem''.

More than 2 samples

Data:

Jargon: ``I levels of some factor influencing the response variable X.''

The idea is that s are results for treatment 1, etc.

Note: in book which is generally a good design.

Model:

• s are all independent.
• are a sample from a population with mean .
• are a sample from a population with mean , and so on.
• All population variances are equal: for all i and j.
• The population distributions are all normal. (But if the are all large, this is not too important.)

Problems of interest:

1. Give confidence intervals for contrasts like , , etc. (A contrast is a linear combination where the coefficients add up to 0.)
2. Give hypothesis tests for .
3. ``Multiple comparisons'' (Several confidence intervals used simultaneously -- what is the overall probability of any errors.)

We do (2) first:

Technique: ANalysis Of VAriance or ANOVA.

Idea: Compare two independent estimates of using an F test.

The theory:

1: In each sample we have an estimate

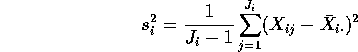
where is notation for the average of the sample:

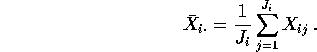
We pool these estimates to get the Mean Square for Error or MSE

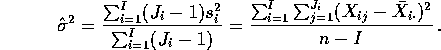
where is the total number of observations in all the samples and I is the number of samples.

2: The other ``estimate of '' is valid only if is true. If and all the then are an iid sample of size I from a population which has a distribution. The sample variance of the is

where now

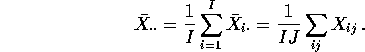
This sample variance is an estimate of the population variance and can be used to estimate by multiplying by n.

Our tests of the hypothesis of no difference between the means to will be based on the ratio of these two estimates of . The crucial factor is that the second estimate of was derived by adding the assumption that the null hypothesis is TRUE so that all the are sampled from the SAME population. One other point is that the restriction that all the sample sizes be equal is not needed, though the second variance estimate then becomes more complicated.