STAT 330 Lecture 16

Reading for Today's Lecture: 8.1, 8.2, 8.3, 9.1, 9.2, 9.4: focus on power and sample size calculations.

Goals of Today's Lecture:

• Learn to compute power of a test: 1 or 2 samples, means or proportions.
• Learn to compute needed sample size: 1 or 2 samples, means or proportions.

Today's notes

Sample Size Calculations

Set

and solve for n. You need to specify:

• 
• true value of the parameters .

Our example had and . So

which happens if

which we solve to get

or

In our example

so that

We round up to n=20 to get the type II error rate to be definitely under 10%.

CRITICISM: the catalyst may very well have changed and will normally be unknown.

You would then use the equation

Notice that n shows up in two places in the formula.

Problem: Solution depends not on the alternative but really on and you need to specify a value for this quantity which is harder to interpret than usually. You then look up versus n in the graph in Appendix A.13. The solution is generally bigger than the formula above for the same value of d.

A two sample example

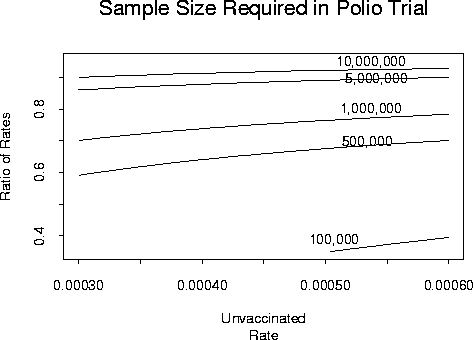
(A calculation of this sort might have been made ahead of the 1954 Salk polio vaccine trials.)

WARNING: Polio is a contagious disease (though not terribly so) and so the independence between people is in grave doubt.

Sample size determination requires the following ingredients:

• 
• 
• likely values for , .

We take and and try various values of in the range of 30 to 50 per 100,000 and in the range of 1 to 40 per 100,000 but in any case with .

We use the usual test statistic with n=m, namely,

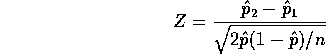
We make the approximation that the value of will be roughly and then compute

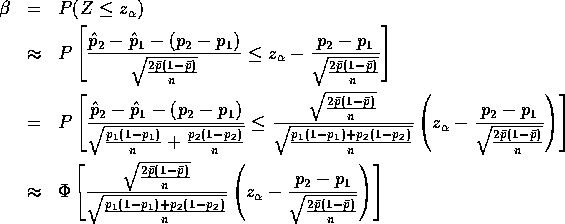
So to find n set

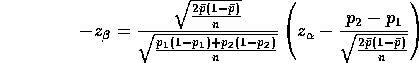
and solve for n. This can be done. Here is a contour plot of the results. The contours indicate combinations of and which require the sample size indicated on the line. Notice that the sample sizes are VERY large.