STAT 330 Lecture 15

Reading for Today's Lecture: 6.2, 8.1, 8.2

Goals of Today's Lecture:

• Learn to compute power of a test.
• Learn to compute needed sample size.

Today's notes

Power, , Sample Size

Definition: the power function of a hypothesis test procedure is

Recall: Type I error is incorrect rejection. Type 2 error is incorrect acceptance.

Definition: The level of a test is the largest probability of rejection for in the null hypothesis:

Typically if the null hypothesis is like the value of is actually , that is, the edge of the null hypothesis gives the highest risk of incorrect rejection.

Definition: The probability of a type two error is a function defined for by

Thus

for not in the Null.

A good test procedure has

• small for .
• large for or, equivalently, small for .

Example 1: iid . {WE PRETEND IS KNOWN.) To test vs at level : reject if

Now

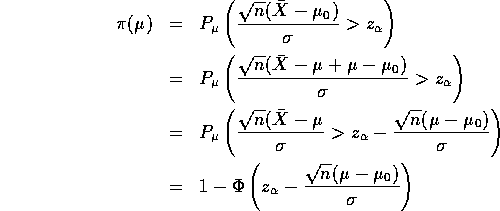
which is the area to the right of

under the standard normal curve. Here is a graph of the power function:

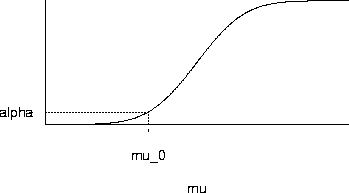
Power and Sample Size Determination

Scenarios:

• Testing a catalyst to improve yields in some chemical production process. How many tests must I run to be sure I detect a difference if it exists?
• Testing a drug: how many patients needed?

In order to determine n you must know:

1. 
2. 
3. Correct alternative distribution, i.e., the value of .

Catalyst example: will be yields for new (catalyzed) method. Assume old method had:

• Mean yield %.
• SD yield %.

Assume new method has mean yield and the same SD 3%.

We will test against at level and reject if

How big should n be? To answer we need to more ingredients:

• A value of whose difference from would be important to detect.
• A tolerable value for the Type II error probability (=1-Power) for this value of .

Suppose manager says would be an important improvement and that a % error rate would be tolerable if . We then solve:

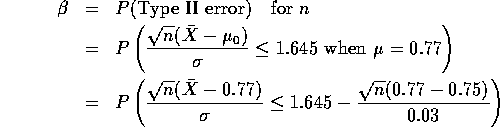
which is the area to the left of

But the area is 10% when

so that the general formula is

or, solving

or

In our example

so that

We round up to n=20 to get the type II error rate to be definitely under 10%.