STAT 330 Lecture 14

Reading for Today's Lecture: 6.2, 8.1, 8.2

Goals of Today's Lecture:

• Learn to find maximum likelihood estimates.
• Introduce power and the probability of a Type II error.

Today's notes

Two general methods to develop estimators:

1. Method of moments: set sample mean equal to population mean, sample second moment equal to population second moment and so on. Solve these equations for . Need 1 equation for each component of .
2. Maximum likelihood: Choose to be the value of which maximizes

   

   This is easier to understand for discrete data.

General framework for MLEs:

If are independent and is the probability mass function for an individual and if we actually observe then the likelihood function is

Example: independent Poisson rvs. So

The likelihood is

It is easier to maximize the logarithm of this:

To do the maximization set the derivative with respect to equal to 0. Get

from which we get

so that is the mle (maximum likelihood estimate) of .

Extension to Continuous Distributions: If are independent and is the probability density of an individual (so that the X's are continuous rvs) then we can interpret the density as follows. Let denote a small positive number. Then

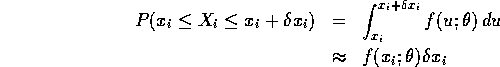
(The equation is the definition of density and the approximation is the meaning of integration over very small intervals -- it expresses the idea that integration is the opposite of differentiation.)

This prompts us to define

and

The MLE of maximizes the Likelihood or equivalently the log likelihood.

Example: a sample from population.

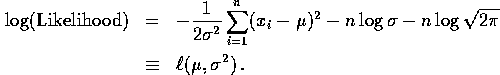
We need to set and to find estimates of and of .

We find:

and

Set to get

so that . Then put this solution in the second equation to get

which produces the solution

Notice that in the denominator there is an n and not n-1. The MLE is not quite the usual estimate of .

Property of MLE

Suppose a different statistician used where as the parameters? What would and be? The log likelihood is now

When you take the derivatives and set them equal to 0 the equation is unchanged and . The derivative with respect to gives the estimate (I leave you to do the algebra)

so that . This is a general principle. If

is a transformation (for some function like say or any other function) of the parameters then the mles satisfy

Power, , Sample Size

Definition: the power function of a hypothesis test procedure is

Recall: Type I error is incorrect rejection. Type 2 error is incorrect acceptance.

Definition: The level of a test is the largest probability of rejection for in the null hypothesis:

Typically if the null hypothesis is like the value of is actually , that is, the edge of the null hypothesis gives the highest risk of incorrect rejection.

Definition: The probability of a type two error is a function defined for by

Thus for not in the Null: