MODEL Statement
- MODEL dependent = < fixed-effects >< / options >;
The MODEL statement names a single dependent variable and
the fixed effects, which determine the X matrix of the
mixed model (see the "Parameterization of Mixed Models" section for details).
The specification of effects is the same as
in the GLM procedure; however, unlike PROC GLM, you do not
specify random effects in the MODEL statement. The MODEL
statement is required.
An intercept is included in the fixed-effects model by default. If
no fixed effects are specified, only this intercept term is fit.
The intercept can be removed by using the NOINT option.
You can specify the following options in the MODEL statement
after a slash (/).
- ALPHA=number
- requests that a t-type confidence interval be constructed for each of
the fixed-effects parameters with confidence level 1-number.
The value of number must be between 0 and 1; the default is 0.05.
- ALPHAP=number
-
requests that a t-type confidence interval be constructed for
the predicted values with confidence level 1-number. The
value of number must be between 0 and 1; the default is 0.05.
- CHISQ
-
requests that
 -tests be performed for all specified effects
in addition to the F-tests. Type III tests are the default;
you can produce the Type I and Type II tests using the
HTYPE= option.
-tests be performed for all specified effects
in addition to the F-tests. Type III tests are the default;
you can produce the Type I and Type II tests using the
HTYPE= option.
- CL
-
requests that t-type confidence limits be constructed for each
of the fixed-effects parameter estimates. The confidence level is
0.95 by default; this can be changed with the
ALPHA= option.
- CONTAIN
-
has the same effect as the DDFM=CONTAIN option.
- CORRB
-
produces the approximate correlation matrix of the fixed-effects
parameter estimates. For ODS purposes, the label for
this table is "CorrB."
- COVB
-
produces the approximate variance-covariance matrix of the
fixed-effects parameter estimates
 . By default,
this matrix equals
. By default,
this matrix equals  and results
from sweeping
and results
from sweeping  on all
but its last pivot and removing the y border. The
EMPIRICAL
option in the PROC MIXED statement changes this matrix into
"empirical sandwich"
form.
For ODS purposes, the label for this table is "CovB."
on all
but its last pivot and removing the y border. The
EMPIRICAL
option in the PROC MIXED statement changes this matrix into
"empirical sandwich"
form.
For ODS purposes, the label for this table is "CovB."
- COVBI
-
produces the inverse of the approximate variance-covariance matrix of
the fixed-effects parameter estimates.
For ODS purposes, the label for this table is "InvCovB."
- DDF=value-list
-
enables you to specify your own denominator degrees of freedom for
the fixed effects. The value-list specification is a list of
numbers or missing values (.) separated by commas. The degrees of
freedom should be listed in the order in which the effects appear in
the "Tests of Fixed Effects" table. If you want to retain
the default degrees of freedom for a particular effect, use a
missing value for its location in the list. For example,
model Y = A B A*B / ddf=3,.,4.7;
assigns 3 denominator degrees of freedom to A and 4.7
to A*B, while those for B remain the same.
- DDFM=CONTAIN
- DDFM=BETWITHIN
- DDFM=RESIDUAL
- DDFM=SATTERTH
- DDFM=KENWARDROGER
-
specifies the method for computing the denominator degrees of
freedom for the tests of fixed effects resulting from the MODEL,
CONTRAST, ESTIMATE, and LSMEANS statements.
The DDFM=CONTAIN option invokes the containment method to
compute denominator degrees of freedom, and it is the default when
you specify a RANDOM statement. The containment method is carried
out as follows: Denote the fixed effect in question A, and
search the RANDOM effect list for the effects that
syntactically contain A. For example, the RANDOM effect
B(A) contains A, but the RANDOM effect C does
not, even if it has the same levels as B(A).
Among the RANDOM effects that contain A, compute their rank
contribution to the (X Z) matrix. The DDF assigned to
A is the smallest of these rank contributions. If no effects are
found, the DDF for A is set equal to the residual degrees of
freedom, N - rank(X Z). This choice of DDF matches
the tests performed for balanced split-plot designs and should be
adequate for moderately unbalanced designs.
Caution: If you have a Z matrix with a large number
of columns, the overall memory requirements and the computing time
after convergence can be substantial for the containment method. If
it is too large, you may want to use the DDFM=BETWITHIN
option.
The DDFM=BETWITHIN
option is the default for REPEATED statement specifications (with no
RANDOM statements). It is computed by dividing the residual degrees
of freedom into between-subject and within-subject portions. PROC
MIXED then checks whether a fixed effect changes within any subject.
If so, it assigns within-subject degrees of freedom to the effect;
otherwise, it assigns the between-subject degrees of freedom to the
effect (refer to Schluchter and Elashoff 1990). If there are
multiple within-subject effects containing classification variables,
the within-subject degrees of freedom is partitioned into components
corresponding to the subject-by-effect interactions.
One exception to the preceding method is the case when you have
specified no RANDOM statements and a REPEATED statement with the
TYPE=UN option. In this case, all effects are assigned the
between-subject degrees of freedom to provide for better small-sample
approximations to the relevant sampling distributions.
The DDFM=RESIDUAL option performs all tests using the residual
degrees of freedom, n - rank(XZ), where n is the
number of observations.
The DDFM=SATTERTH option performs a general Satterthwaite
approximation for the denominator degrees of freedom, computed as
follows. Let C = (X'V-1X)-, where - denotes a generalized
inverse, and let 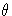 be the vector of unknown parameters in V.
Let
be the vector of unknown parameters in V.
Let  and
and  be the corresponding estimates.
be the corresponding estimates.
We first consider the one-dimensional case, and
consider l to be a vector defining an estimable
linear combination of  .The Satterthwaite degrees of freedom for the t-statistic
.The Satterthwaite degrees of freedom for the t-statistic

is computed as
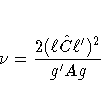
where g is the gradient of lC l' with respect to 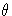 ,evaluated at
,evaluated at  ,and A is the asymptotic variance-covariance matrix of
,and A is the asymptotic variance-covariance matrix of  obtained from the second derivative matrix of the likelihood equations.
obtained from the second derivative matrix of the likelihood equations.
For the multi-dimensional case,
let L be an estimable contrast matrix of rank q > 1.
The Satterthwaite denominator degrees of freedom for the F-statistic

is computed by first performing the spectral decomposition
 where P is an orthogonal matrix of eigenvectors and D is
a diagonal matrix of eigenvalues, both of dimension q ×q.
Define lm to be the mth row of PL, and
let
where P is an orthogonal matrix of eigenvectors and D is
a diagonal matrix of eigenvalues, both of dimension q ×q.
Define lm to be the mth row of PL, and
let

where Dm is the mth diagonal element of D and
gm is the gradient of lm C lm' with respect to 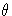 ,evaluated at
,evaluated at  .
Then let
.
Then let

where the indicator function eliminates terms for which
 .The degrees of freedom for F are then
computed as
.The degrees of freedom for F are then
computed as
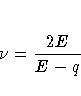
provided E > q; otherwise  is set to zero.
is set to zero.
This method is a generalization of the techniques described in
Giesbrecht and Burns (1985), McLean and Sanders (1988), and Fai and
Cornelius (1996). The method can also include estimated random
effects. In this case, append  to
to 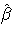 and
change
and
change  to be the inverse of the coefficient matrix in the
mixed model equations. The calculations require extra memory to hold
c matrices that are the size of the mixed model equations, where c
is the number of covariance parameters. In the notation of
Table 41.9, this is approximately 8q(p+g)(p+g)/2
bytes. Extra computing time is also required to process these
matrices. The Satterthwaite method implemented here is intended to
produce an accurate F-approximation; however, the results may
differ from those produced by PROC GLM. Also, the small sample
properties of this approximation have not been extensively
investigated for the various models available with PROC MIXED.
to be the inverse of the coefficient matrix in the
mixed model equations. The calculations require extra memory to hold
c matrices that are the size of the mixed model equations, where c
is the number of covariance parameters. In the notation of
Table 41.9, this is approximately 8q(p+g)(p+g)/2
bytes. Extra computing time is also required to process these
matrices. The Satterthwaite method implemented here is intended to
produce an accurate F-approximation; however, the results may
differ from those produced by PROC GLM. Also, the small sample
properties of this approximation have not been extensively
investigated for the various models available with PROC MIXED.
The DDFM=KENWARDROGER option performs the degrees-of-freedom
calculations detailed by Kenward and Roger (1997). This approximation
involves inflating the estimated variance-covariance matrix of the
fixed and random effects by the method proposed by Prasad and Rao
(1990) and Harville and Jeske (1992); refer also to Kackar and
Harville (1984). Satterthwaite-type degrees of freedom are then
computed based on this adjustment. By default, the observed
information matrix of the covariance parameter estimates is used
in the calculations.
This method changes output in the following tables (listed in
Table 41.7): Contrast, CorrB, CovB, Diffs, Estimates,
InvCovB, LSMeans, MMEq, MMEqSol, Slices, SolutionF, SolutionR,
Tests1 -Tests3. The OUTP= and OUTPM= data sets are also
affected.
- E
-
requests that Type I, Type II, and Type III L matrix coefficients
be displayed for all specified effects. For ODS purposes, the labels
of the tables are "Coefficients".
- E1
-
requests that Type I L matrix coefficients be displayed for all
specified effects. For ODS purposes, the label of this table is
"Coefficients".
- E2
-
requests that Type II L matrix coefficients be displayed for all
specified effects. For ODS purposes, the label of this table is
"Coefficients".
- E3
-
requests that Type III L matrix coefficients be displayed for all
specified effects. For ODS purposes, the label of this table is
"Coefficients".
- FULLX
-
requests that columns of the X matrix that consist entirely of zeros
not be eliminated from X; they are eliminated by default.
For a column corresponding to a missing cell to be added to X, its
particular levels must be present in at least one observation in the
analysis data set along with a missing dependent variable. The use of
the FULLX option can impact coefficient specifications in the CONTRAST and
ESTIMATE statements, as well as covariate coefficients from LSMEANS
statements specified with the AT MEANS option.
- HTYPE=value-list
-
indicates the type of hypothesis test to perform on the fixed
effects. Valid entries for value are 1, 2, and 3; the default
value is 3. You can specify several types by separating the values
with a comma or a space. The ODS table names are "Tests1" for the
Type 1 tests, "Tests2" for the Type 2 tests, and "Tests3" for Type 3
tests.
- NOCONTAIN
-
has the same effect as the DDFM=RESIDUAL option.
- NOINT
-
requests that no intercept be included in the model. An intercept
is included by default.
- NOTEST
-
specifies that no hypothesis tests be performed for the fixed
effects.
- OUTP=SAS-data-set
- OUTPRED=SAS-data-set
-
specifies an output data set containing predicted values and related
quantities. This option replaces the P option from Version 6.
Predicted values are formed by using the rows from (X Z) as
L matrices. The predicted values from the original data are,
thus,  . Their
approximate standard errors of prediction are formed from the
quadratic form of L with
. Their
approximate standard errors of prediction are formed from the
quadratic form of L with  defined in
the "Statistical Properties" section. The L95
and U95 variables provide a t-type confidence interval for the
predicted values, and they correspond to the L95M and U95M
variables from the GLM and REG procedures for fixed-effect models.
The residuals are the observed minus the predicted values.
Predicted values for data points other than those observed can be
obtained by using missing dependent variables in your input data
set.
defined in
the "Statistical Properties" section. The L95
and U95 variables provide a t-type confidence interval for the
predicted values, and they correspond to the L95M and U95M
variables from the GLM and REG procedures for fixed-effect models.
The residuals are the observed minus the predicted values.
Predicted values for data points other than those observed can be
obtained by using missing dependent variables in your input data
set.
Specifications that have a REPEATED
statement with the SUBJECT= option and missing dependent variables
compute predicted values using empirical best
linear unbiased prediction (EBLUP).
Using hats  to
denote estimates, the EBLUP formula is
to
denote estimates, the EBLUP formula is

where m represents a hypothetical realization of a missing data
vector with associated design matrix Xm. The matrix Cm is the
model-based covariance matrix between m and the observed data
y, and other notation is as presented in
the "Mixed Models Theory" section.
The estimated prediction variance is as follows:
![\hat{Var}(\hat{m} - m) &=& \hat{V}_{m}-
\hat{C}_{m}\hat{V}^{-1} \hat{C}_{m}^T +...
...\hat{V}^{-1} X]
( X^T \hat{V}^{-1} X)^-
[X_{m}- \hat{C}_{m}\hat{V}^{-1} X]^T](images/mixeq67.gif)
where Vm is the model-based variance matrix of m. For
further details, refer to Henderson (1984) and Harville (1990).
This feature can be useful for forecasting time series or for
computing spatial predictions.
By default, all variables from the input data set are included in
the OUTP= data set. You can select a subset of these variables
using the ID statement.
- OUTPM=SAS-data-set
- OUTPREDM=SAS-data-set
-
specifies an output data set containing predicted means and related
quantities. This option replaces the PM option from Version 6.
The output data set is of the same form as that resulting from the
OUTP= option, except that the predicted values do not incorporate
the EBLUP values  nor do they use the EBLUPs
for specifications that have a REPEATED statement with the SUBJECT=
option and missing dependent variables. The predicted values are
formed as
nor do they use the EBLUPs
for specifications that have a REPEATED statement with the SUBJECT=
option and missing dependent variables. The predicted values are
formed as 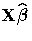 in the OUTPM= data set, and standard
errors are quadratic forms in the approximate variance-covariance
matrix of
in the OUTPM= data set, and standard
errors are quadratic forms in the approximate variance-covariance
matrix of  as displayed by the COVB option.
as displayed by the COVB option.
By default, all variables from the input data set are included in
the OUTPM= data set. You can select a subset of these variables
using the ID statement.
- SINGULAR=number
-
tunes the sensitivity in sweeping. If a diagonal pivot element is
less than D*number as PROC MIXED sweeps a matrix, the
associated column is declared to be linearly dependent upon previous
columns, and the associated parameter is set to 0. The value D is the
original diagonal element of the matrix. The default is 1E4 times
the machine epsilon; this product is approximately 1E-12 on most
computers.
- SINGCHOL=number
-
tunes the sensitivity in computing Cholesky roots. If a diagonal
pivot element is less than D*number as PROC MIXED performs the
Cholesky decomposition on a matrix, the associated column is
declared to be linearly dependent upon previous columns and is set
to 0. The value D is the original diagonal element of the matrix. The
default for number is 1E4 times the machine epsilon; this
product is approximately 1E-12 on most computers.
- SINGRES=number
-
sets the tolerance for which the residual variance is considered to
be zero. The default is 1E4 times the machine epsilon; this product
is approximately 1E-12 on most computers.
- SOLUTION
- S
-
requests that a solution for the fixed-effects parameters be
produced. Using notation from
the "Mixed Models Theory" section, the fixed-effects parameter estimates are
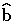 and their approximate standard errors are the
square roots of the diagonal elements of
and their approximate standard errors are the
square roots of the diagonal elements of  . You can output this approximate variance matrix with the
COVB option or modify it with the
EMPIRICAL option in the PROC MIXED
statement.
. You can output this approximate variance matrix with the
COVB option or modify it with the
EMPIRICAL option in the PROC MIXED
statement.
Along with the estimates and their approximate standard errors, a
t-statistic is computed as the estimate divided by its
standard error. The degrees of freedom for this t-statistic
matches the one appearing in the "Tests of Fixed Effects" table under
the effect containing the parameter. The "Pr > |t|"
column contains the
two-tailed p-value corresponding to the t-statistic and
associated degrees of freedom. You can use the
CL option to request
confidence intervals for all of the parameters; they are constructed
around the estimate by using a radius of the standard error times a
percentage point from the t-distribution.
- XPVIX
-
is an alias for the COVBI option.
- XPVIXI
-
is an alias for the COVB option.
- ZETA=number
-
tunes the sensitivity in forming Type III functions.
Any element in the estimable function basis with an absolute
value less than number is set to 0.
The default is 1E-8.
Copyright © 1999 by SAS Institute Inc., Cary, NC, USA. All rights reserved.

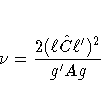



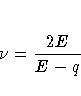

![\hat{Var}(\hat{m} - m) &=& \hat{V}_{m}-
\hat{C}_{m}\hat{V}^{-1} \hat{C}_{m}^T +...
...\hat{V}^{-1} X]
( X^T \hat{V}^{-1} X)^-
[X_{m}- \hat{C}_{m}\hat{V}^{-1} X]^T](images/mixeq67.gif)