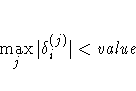MODEL Statement

The LOGISTIC Procedure

MODEL Statement

MODEL variable= < effects > < /options >;

MODEL events/trials= < effects > < / options >;

The MODEL statement names the response variable and the explanatory effects, including covariates, main effects, interactions, and nested effects. If you omit the explanatory variables, the procedure fits an intercept-only model.

Two forms of the MODEL statement can be specified. The first form, referred to as single-trial syntax, is applicable to both binary response data and ordinal response data. The second form, referred to as events/trials syntax, is restricted to the case of binary response data. The single-trial syntax is used when each observation in the DATA= data set contains information on only a single trial, for instance, a single subject in an experiment. When each observation contains information on multiple binary-response trials, such as the counts of the number of subjects observed and the number responding, then events/trials syntax can be used.

In the single-trial syntax, you specify one variable (preceding the equal sign) as the response variable. This variable can be character or numeric. Values of this variable are sorted by the ORDER= option (and the DESCENDING option, if specified) in the PROC LOGISTIC statement.

In the events/trials syntax, you specify two variables that contain count data for a binomial experiment. These two variables are separated by a slash. The value of the first variable, events, is the number of positive responses (or events). The value of the second variable, trials, is the number of trials. The values of both events and (trials-events) must be nonnegative and the value of trials must be positive for the response to be valid.

For both forms of the MODEL statement, explanatory effects follow the equal sign. The variables can be either continuous or classification variables. Classification variables can be character or numeric, and they must be declared in the CLASS statement. When an effect is a classification variable, the procedure enters a set of coded columns into the design matrix instead of directly entering a single column containing the values of the variable. See the section "Specification of Effects" of Chapter 30, "The GLM Procedure."

Table 39.1 summarizes the options available in the MODEL statement.

Table 39.1: Model Statement Options

Option	Description
Model Specification Options
LINK=	specifies link function
NOINT	suppresses intercept
NOFIT	suppresses model fitting
OFFSET=	specifies offset variable
SELECTION=	specifies variable selection method
Variable Selection Options
BEST=	controls the number of models displayed for SCORE selection
DETAILS	requests detailed results at each step
FAST	uses fast elimination method
HIERARCHY=	specifies whether and how hierarchy is maintained and whether a single effect or multiple effects are allowed to enter or leave the model per step
INCLUDE=	specifies number of variables included in every model
MAXSTEP=	specifies maximum number of steps for STEPWISE selection
SEQUENTIAL	adds or deletes variables in sequential order
SLENTRY=	specifies significance level for entering variables
SLSTAY=	specifies significance level for removing variables
START=	specifies the number of variables in first model
STOP=	specifies the number of variables in final model
STOPRES	adds or deletes variables by residual chi-square criterion
Model-Fitting Specification Options
ABSFCONV=	specifies the absolute function convergence criterion
FCONV=	specifies the relative function convergence criterion
GCONV=	specifies the relative gradient convergence criterion
XCONV=	specifies the relative parameter convergence criterion
MAXITER=	specifies maximum number of iterations
NOCHECK	suppresses checking for infinite parameters
RIDGING=	specifies the technique used to improve the log-likelihood function when its value is worse than that of the previous step
SINGULAR=	specifies tolerance for testing singularity
TECHNIQUE=	specifies iterative algorithm for maximization
Options for Confidence Intervals
ALPHA=	specifies $\alpha$ for the $100(1-\alpha)\%$ confidence intervals
CLPARM=	computes confidence intervals for parameters
CLODDS=	computes confidence intervals for odds ratios
PLCONV=	specifies profile likelihood convergence criterion
Options for Classifying Observations
CTABLE	displays classification table
PEVENT=	specifies prior event probabilities
PPROB=	specifies probability cutpoints for classification
Options for Overdispersion and Goodness-of-Fit Tests
AGGREGATE=	determines subpopulations for Pearson chi-square and deviance
SCALE=	species method to correct overdispersion
LACKFIT	requests Hosmer and Lemeshow goodness-of-fit test
Options for ROC Curves
OUTROC=	names the output data set
ROCEPS=	specifies probability grouping criterion
Options for Regression Diagnostics
INFLUENCE	displays influence statistics
IPLOTS	requests index plots
Options for Display of Details
CORRB	displays correlation matrix
COVB	displays covariance matrix
EXPB	displays the exponentiated values of estimates
ITPRINT	displays iteration history
NODUMMYPRINT	suppresses the "Class Level Information" table
PARMLABEL	displays the parameter labels
RSQUARE	displays generalized R²
STB	displays the standardized estimates

The following list describes these options.

ABSFCONV=value

specifies the absolute function convergence criterion. Convergence requires a small change in the log-likelihood function in subsequent iterations,

$| l_i - l_{i-1}| \lt {value}$

where l_i is the value of the log-likelihood function at iteration i. See the section "Convergence Criteria".

AGGREGATE

AGGREGATE= (variable-list)

specifies the subpopulations on which the Pearson chi-square test statistic and the likelihood ratio chi-square test statistic (deviance) are calculated. Observations with common values in the given list of variables are regarded as coming from the same subpopulation. Variables in the list can be any variables in the input data set. Specifying the AGGREGATE option is equivalent to specifying the AGGREGATE= option with a variable list that includes all explanatory variables in the MODEL statement. The deviance and Pearson goodness-of-fit statistics are calculated only when the SCALE= option is specified. Thus, the AGGREGATE (or AGGREGATE=) option has no effect if the SCALE= option is not specified. See the section "Rescaling the Covariance Matrix" for more detail.

ALPHA=value

sets the significance level for the confidence intervals for regression parameters or odds ratios. The value must be between 0 and 1. The default value of 0.05 results in the calculation of a 95% confidence interval. This option has no effect unless confidence limits for the parameters or odds ratios are requested.

BEST=n

specifies that n models with the highest score chi-square statistics are to be displayed for each model size. It is used exclusively with the SCORE model selection method. If the BEST= option is omitted and there are no more than ten explanatory variables, then all possible models are listed for each model size. If the option is omitted and there are more than ten explanatory variables, then the number of models selected for each model size is, at most, equal to the number of explanatory variables listed in the MODEL statement.

CLODDS=PL | WALD | BOTH

requests confidence intervals for the odds ratios. Computation of these confidence intervals is based on the profile likelihood (CLODDS=PL) or based on individual Wald tests (CLODDS=WALD). By specifying CLPARM=BOTH, the procedure computes two sets of confidence intervals for the odds ratios, one based on the profile likelihood and the other based on the Wald tests. The confidence coefficient can be specified with the ALPHA= option.

CLPARM=PL | WALD | BOTH

requests confidence intervals for the parameters. Computation of these confidence intervals is based on the profile likelihood (CLPARM=PL) or individual Wald tests (CLPARM=WALD). By specifying CLPARM=BOTH, the procedure computes two sets of confidence intervals for the parameters, one based on the profile likelihood and the other based on individual Wald tests. The confidence coefficient can be specified with the ALPHA= option. See the "Confidence Intervals for Parameters" section for more information.

CONVERGE=value

is the same as specifying the XCONV= option.

CORRB

displays the correlation matrix of the parameter estimates.

COVB

displays the covariance matrix of the parameter estimates.

CTABLE

classifies the input binary response observations according to whether the predicted event probabilities are above or below some cutpoint value z in the range (0,1). An observation is predicted as an event if the predicted event probability exceeds z. You can supply a list of cutpoints other than the default list by using the PPROB= option. The CTABLE option is ignored if the data have more than two response levels. Also, false positive and negative rates can be computed as posterior probabilities using Bayes' theorem. You can use the PEVENT= option to specify prior probabilities for computing these rates. For more information, see the "Classification Table" section.

DETAILS

produces a summary of computational details for each step of the variable selection process. It produces the "Analysis of Effects Not in the Model" table before displaying the effect selected for entry for FORWARD or STEPWISE selection. For each model fitted, it produces the "Type III Analysis of Effects" table if the fitted model involves CLASS variables, the "Analysis of Maximum Likelihood Estimates" table, and measures of association between predicted probabilities and observed responses. For the statistics included in these tables, see the "Displayed Output" section. The DETAILS option has no effect when SELECTION=NONE.

EXPB

EXPEST

displays the exponentiated values (e $^{\hat{\beta}_i}$ ) of the parameter estimates $\hat{\beta_i}$ in the "Analysis of Maximum Likelihood Estimates" table for the logit model. These exponentiated values are the estimated odds ratios for the parameters corresponding to the continuous explanatory variables.

FAST

uses a computational algorithm of Lawless and Singhal (1978) to compute a first-order approximation to the remaining slope estimates for each subsequent elimination of a variable from the model. Variables are removed from the model based on these approximate estimates. The FAST option is extremely efficient because the model is not refitted for every variable removed. The FAST option is used when SELECTION=BACKWARD and in the backward elimination steps when SELECTION=STEPWISE. The FAST option is ignored when SELECTION=FORWARD or SELECTION=NONE.

FCONV=value

specifies the relative function convergence criterion. Convergence requires a small relative change in the log-likelihood function in subsequent iterations,

$\frac{ | l_i - l_{i-1}|} {| l_{i-1}| + {{1E-6}}} \lt {value}$

where l_i is the value of the log-likelihood at iteration i. See the section "Convergence Criteria".

GCONV=value

specifies the relative gradient convergence criterion. Convergence requires that the normalized prediction function reduction is small,

$\frac{g_i^' H_i g_i} {| l_i| + {{1E-6}}} \lt {value}$

where l_i is value of the log-likelihood function, g_i is the gradient vector, and H_i is the negative (expected) Hessian matrix, all at iteration i. This is the default convergence criterion, and the default value is 1E-8. See the section "Convergence Criteria".

HIERARCHY=keyword

HIER=keyword

specifies whether and how the model hierarchy requirement is applied and whether a single effect or multiple effects are allowed to enter or leave the model in one step. You can specify that only CLASS effects, or both CLASS and interval effects, be subject to the hierarchy requirement. The HIERARCHY= option is ignored unless you also specify one of the following options: SELECTION=FORWARD, SELECTION=BACKWARD, or SELECTION=STEPWISE.

Model hierarchy refers to the requirement that, for any term to be in the model, all effects contained in the term must be present in the model. For example, in order for the interaction A*B to enter the model, the main effects A and B must be in the model. Likewise, neither effect A nor B can leave the model while the interaction A*B is in the model.

The keywords you can specify in the HIERARCHY= option are described as follows:

NONE
: Model hierarchy is not maintained. Any single effect can enter or leave the model at any given step of the selection process.
SINGLE
: Only one effect can enter or leave the model at one time, subject to the model hierarchy requirement. For example, suppose that you specify the main effects A and B and the interaction of A*B in the model. In the first step of the selection process, either A or B can enter the model. In the second step, the other main effect can enter the model. The interaction effect can enter the model only when both main effects have already been entered. Also, before A or B can be removed from the model, the A*B interaction must first be removed. All effects (CLASS and interval) are subject to the hierarchy requirement.
SINGLECLASS
: This is the same as HIERARCHY=SINGLE except that only CLASS effects are subject to the hierarchy requirement.
MULTIPLE
: More than one effect can enter or leave the model at one time, subject to the model hierarchy requirement. In a forward selection step, a single main effect can enter the model, or an interaction can enter the model together with all the effects that are contained in the interaction. In a backward elimination step, an interaction itself, or the interaction together with all the effects that the interaction contains, can be removed. All effects (CLASS and interval) are subject to the hierarchy requirement.
MULTIPLECLASS
: This is the same as HIERARCHY=MULTIPLE except that only CLASS effects are subject to the hierarchy requirement.

The default value is HIERARCHY=SINGLE, which means that model hierarchy is to be maintained for all effects (that is, both CLASS and interval effects) and that only a single effect can enter or leave the model at each step.

INCLUDE=n

includes the first n effects in the MODEL statement in every model. By default, INCLUDE=0. The INCLUDE= option has no effect when SELECTION=NONE.

Note that the INCLUDE= and START= options perform different tasks: the INCLUDE= option includes the first n effects variables in every model, whereas the START= option only requires that the first n effects appear in the first model.

INFLUENCE

displays diagnostic measures for identifying influential observations in the case of a binary response model. It has no effect otherwise. For each observation, the INFLUENCE option displays the case number (which is the sequence number of the observation), the values of the explanatory variables included in the final model, and the regression diagnostic measures developed by Pregibon (1981). For a discussion of these diagnostic measures, see the "Regression Diagnostics" section.

IPLOTS

produces an index plot for each regression diagnostic statistic. An index plot is a scatterplot with the regression diagnostic statistic represented on the y-axis and the case number on the x-axis. See Example 39.4 for an illustration.

ITPRINT

displays the iteration history of the maximum-likelihood model fitting. The ITPRINT option also displays the last evaluation of the gradient vector and the final change in the -2 Log Likelihood.

LACKFIT

LACKFIT<(n)>

performs the Hosmer and Lemeshow goodness-of-fit test (Hosmer and Lemeshow 1989) for the case of a binary response model. The subjects are divided into approximately ten groups of roughly the same size based on the percentiles of the estimated probabilities. The discrepancies between the observed and expected number of observations in these groups are summarized by the Pearson chi-square statistic, which is then compared to a chi-square distribution with t degrees of freedom, where t is the number of groups minus n. By default, n=2. A small p-value suggests that the fitted model is not an adequate model.

LINK=CLOGLOG | LOGIT | PROBIT

L=CLOGLOG | LOGIT | PROBIT

specifies the link function for the response probabilities. CLOGLOG is the complementary log-log function, LOGIT is the log odds function, and PROBIT (or NORMIT) is the inverse standard normal distribution function. By default, LINK=LOGIT. See the section "Link Functions and the Corresponding Distributions" for details.

MAXITER=n

specifies the maximum number of iterations to perform. By default, MAXITER=25. If convergence is not attained in n iterations, the displayed output and all output data sets created by the procedure contain results that are based on the last maximum likelihood iteration.

MAXSTEP=n

specifies the maximum number of times any explanatory variable is added to or removed from the model when SELECTION=STEPWISE. The default number is twice the number of explanatory variables in the MODEL statement. When the MAXSTEP= limit is reached, the stepwise selection process is terminated. All statistics displayed by the procedure (and included in output data sets) are based on the last model fitted. The MAXSTEP= option has no effect when SELECTION=NONE, FORWARD, or BACKWARD.

NOCHECK

disables the checking process to determine whether maximum likelihood estimates of the regression parameters exist. If you are sure that the estimates are finite, this option can reduce the execution time if the estimation takes more than eight iterations. For more information, see the "Existence of Maximum Likelihood Estimates" section.

NODUMMYPRINT

NODESIGNPRINT

NODP

suppresses the "Class Level Information" table, which shows how the design matrix columns for the CLASS variables are coded.

NOINT

suppresses the intercept for the binary response model or the first intercept for the ordinal response model. This can be particularly useful in conditional logistic analysis; see Example 39.9.

NOFIT

performs the global score test without fitting the model. The global score test evaluates the joint significance of the effects in the MODEL statement. No further analyses are performed. If the NOFIT option is specified along with other MODEL statement options, NOFIT takes effect and all other options except LINK=, TECHNIQUE=, and OFFSET= are ignored.

OFFSET= name

names the offset variable. The regression coefficient for this variable will be fixed at 1.

OUTROC=SAS-data-set

OUTR=SAS-data-set

creates, for binary response models, an output SAS data set that contains the data necessary to produce the receiver operating characteristic (ROC) curve. See the section "OUTROC= Data Set" for the list of variables in this data set.

PARMLABEL

displays the labels of the parameters in the "Analysis of Maximum Likelihood Estimates" table.

PEVENT= value

PEVENT= (list )

specifies one prior probability or a list of prior probabilities for the event of interest. The false positive and false negative rates are then computed as posterior probabilities by Bayes' theorem. The prior probability is also used in computing the rate of correct prediction. For each prior probability in the given list, a classification table of all observations is computed. By default, the prior probability is the total sample proportion of events. The PEVENT= option is useful for stratified samples. It has no effect if the CTABLE option is not specified. For more information, see the section "False Positive and Negative Rates Using Bayes' Theorem". Also see the PPROB= option for information on how the list is specified.

PLCL

is the same as specifying CLPARM=PL.

PLCONV= value

controls the convergence criterion for confidence intervals based on the profile likelihood function. The quantity value must be a positive number, with a default value of 1E-4. The PLCONV= option has no effect if profile likelihood confidence intervals (CLPARM=PL) are not requested.

PLRL

is the same as specifying CLODDS=PL.

PPROB=value

PPROB= (list )

specifies one critical probability value (or cutpoint) or a list of critical probability values for classifying observations with the CTABLE option. Each value must be between 0 and 1. A response that has a crossvalidated predicted probability greater than or equal to the current PPROB= value is classified as an event response. The PPROB= option is ignored if the CTABLE option is not specified.

A classification table for each of several cutpoints can be requested by specifying a list. For example,

   pprob= (0.3, 0.5 to 0.8 by 0.1)

requests a classification of the observations for each of the cutpoints 0.3, 0.5, 0.6, 0.7, and 0.8. If the PPROB= option is not specified, the default is to display the classification for a range of probabilities from the smallest estimated probability (rounded below to the nearest 0.02) to the highest estimated probability (rounded above to the nearest 0.02) with 0.02 increments.

RIDGING=ABSOLUTE | RELATIVE | NONE

specifies the technique used to improve the log-likelihood function when its value in the current iteration is less than that in the previous iteration. If you specify the RIDGING=ABSOLUTE option, the diagonal elements of the negative (expected) Hessian are inflated by adding the ridge value. If you specify the RIDGING=RELATIVE option, the diagonal elements are inflated by a factor of 1 plus the ridge value. If you specify the RIDGING=NONE option, the crude line search method of taking half a step is used instead of ridging. By default, RIDGING=RELATIVE.

RISKLIMITS

RL

WALDRL

is the same as specifying CLODDS=WALD.

ROCEPS= number

specifies the criterion for grouping estimated event probabilities that are close to each other for the ROC curve. In each group, the difference between the largest and the smallest estimated event probabilities does not exceed the given value. The default is 1E-4. The smallest estimated probability in each group serves as a cutpoint for predicting an event response. The ROCEPS= option has no effect if the OUTROC= option is not specified.

RSQUARE

RSQ

requests a generalized R² measure for the fitted model. For more information, see the "Generalized Coefficient of Determination" section.

SCALE= scale

enables you to supply the value of the dispersion parameter or to specify the method for estimating the dispersion parameter. It also enables you to display the "Deviance and Pearson Goodness-of-Fit Statistics" table. To correct for overdispersion or underdispersion, the covariance matrix is multiplied by the estimate of the dispersion parameter. Valid values for scale are as follows:

D | DEVIANCE: specifies that the dispersion parameter be estimated by the deviance divided by its degrees of freedom.
P | PEARSON: specifies that the dispersion parameter be estimated by the Pearson chi-square statistic divided by its degrees of freedom.
WILLIAMS <(constant)>: specifies that Williams' method be used to model overdispersion. This option can be used only with the events/trials syntax. An optional constant can be specified as the scale parameter; otherwise, a scale parameter is estimated under the full model. A set of weights is created based on this scale parameter estimate. These weights can then be used in fitting subsequent models of fewer terms than the full model. When fitting these submodels, specify the computed scale parameter as constant. See Example 39.8 for an illustration.
N | NONE: specifies that no correction is needed for the dispersion parameter; that is, the dispersion parameter remains as 1. This specification is used for requesting the deviance and the Pearson chi-square statistic without adjusting for overdispersion.
constant: sets the estimate of the dispersion parameter to be the square of the given constant. For example, SCALE=2 sets the dispersion parameter to 4. The value constant must be a positive number.

You can use the AGGREGATE (or AGGREGATE=) option to define the subpopulations for calculating the Pearson chi-square statistic and the deviance. In the absence of the AGGREGATE (or AGGREGATE=) option, each observation is regarded as coming from a different subpopulation. For the events/trials syntax, each observation consists of n Bernoulli trials, where n is the value of the trials variable. For single-trial syntax, each observation consists of a single response, and for this setting it is not appropriate to carry out the Pearson or deviance goodness-of-fit analysis. Thus, PROC LOGISTIC ignores specifications SCALE=P, SCALE=D, and SCALE=N when single-trial syntax is specified without the AGGREGATE (or AGGREGATE=) option.

The "Deviance and Pearson Goodness-of-Fit Statistics" table includes the Pearson chi-square statistic, the deviance, their degrees of freedom, the ratio of each statistic divided by its degrees of freedom, and the corresponding p-value. For more information, see the "Overdispersion" section.

SELECTION=BACKWARD | B

| FORWARD | F

| NONE | N

| STEPWISE | S

| SCORE

specifies the method used to select the variables in the model. BACKWARD requests backward elimination, FORWARD requests forward selection, NONE fits the complete model specified in the MODEL statement, and STEPWISE requests stepwise selection. SCORE requests best subset selection. By default, SELECTION=NONE. For more information, see the "Effect Selection Methods" section.

SEQUENTIAL

SEQ

forces effects to be added to the model in the order specified in the MODEL statement or eliminated from the model in the reverse order specified in the MODEL statement. The model-building process continues until the next effect to be added has an insignificant adjusted chi-square statistic or until the next effect to be deleted has a significant Wald chi-square statistic. The SEQUENTIAL option has no effect when SELECTION=NONE.

SINGULAR=value

specifies the tolerance for testing the singularity of the Hessian matrix (Newton-Raphson algorithm) or the expected value of the Hessian matrix (Fisher-scoring algorithm). The Hessian matrix is the matrix of second partial derivatives of the log likelihood. The test requires that a pivot for sweeping this matrix be at least this number times a norm of the matrix. Values of the SINGULAR= option must be numeric. By default, SINGULAR=1E-12.

SLENTRY=value

SLE=value

specifies the significance level of the score chi-square for entering an effect into the model in the FORWARD or STEPWISE method. Values of the SLENTRY= option should be between 0 and 1, inclusive. By default, SLENTRY=0.05. The SLENTRY= option has no effect when SELECTION=NONE, SELECTION=BACKWARD, or SELECTION=SCORE.

SLSTAY=value

SLS=value

specifies the significance level of the Wald chi-square for an effect to stay in the model in a backward elimination step. Values of the SLSTAY= option should be between 0 and 1, inclusive. By default, SLSTAY=0.05. The SLSTAY= option has no effect when SELECTION=NONE, SELECTION=FORWARD, or SELECTION=SCORE.

START=n

begins the FORWARD, BACKWARD, or STEPWISE effect selection process with the first n effects listed in the MODEL statement. The value of n ranges from 0 to s, where s is the total number of effects in the MODEL statement. The default value of n is s for the BACKWARD method and 0 for the FORWARD and STEPWISE methods. Note that START=n specifies only that the first n effects appear in the first model, while INCLUDE=n requires that the first n effects be included in every model. For the SCORE method, START=n specifies that the smallest models contain n effects, where n ranges from 1 to s; the default value is 1. The START= option has no effect when SELECTION=NONE.

STB

displays the standardized estimates for the parameters for the continuous explanatory variables in the "Analysis of Maximum Likelihood Estimates" table. The standardized estimate of $\beta_i$ is given by $\hat{\beta}_i/(s/s_i)$ , where s_i is the total sample standard deviation for the ith explanatory variable and

$s= \{ \pi/\sqrt{3} & {Logistic} \ 1 & {Normal} \ \pi/\sqrt{6} & {Extreme-value} .$

For the intercept parameters and parameters associated with a CLASS variable, the standardized estimates are set to missing.

STOP=n

specifies the maximum (FORWARD method) or minimum (BACKWARD method) number of effects to be included in the final model. The effect selection process is stopped when n effects are found. The value of n ranges from 0 to s, where s is the total number of effects in the MODEL statement. The default value of n is s for the FORWARD method and 0 for the BACKWARD method. For the SCORE method, START=n specifies that the smallest models contain n effects, where n ranges from 1 to s; the default value of n is s. The STOP= option has no effect when SELECTION=NONE or STEPWISE.

STOPRES

SR

specifies that the removal or entry of effects be based on the value of the residual chi-square. If SELECTION=FORWARD, then the STOPRES option adds the effects into the model one at a time until the residual chi-square becomes insignificant (until the p-value of the residual chi-square exceeds the SLENTRY= value). If SELECTION=BACKWARD, then the STOPRES option removes effects from the model one at a time until the residual chi-square becomes significant (until the p-value of the residual chi-square becomes less than the SLSTAY= value). The STOPRES option has no effect when SELECTION=NONE or SELECTION=STEPWISE.

TECHNIQUE=FISHER | NEWTON

TECH=FISHER | NEWTON

specifies the optimization technique for estimating the regression parameters. NEWTON (or NR) is the Newton-Raphson algorithm and FISHER (or FS) is the Fisher-scoring algorithm. Both techniques yield the same estimates, but the estimated covariance matrices are slightly different except for the case when the LOGIT link is specified for binary response data. The default is TECHNIQUE=FISHER. See the section "Iterative Algorithms for Model-Fitting" for details.

WALDCL

CL

is the same as specifying CLPARM=WALD.

XCONV=value

specifies the relative parameter convergence criterion. Convergence requires a small relative parameter change in subsequent iterations,

$\max_j |\delta_i^{(j)}| \lt {value}$

where

$\delta_i^{(j)} = \{ \theta_i^{(j)} - \theta_{i-1}^{(j)} & |\theta_{i-1}^{(j)}|... ...{\theta_i^{(j)} - \theta_{i-1}^{(j)}}{\theta_{i-1}^{(j)} } & {\rm otherwise} .$

and $\theta_i^{(j)}$ is the estimate of the jth parameter at iteration i. See the section "Convergence Criteria".

Chapter Contents
Previous
Next
Top