The following entries provide detailed descriptions of
options for the HISTOGRAM statement.
- ALPHA=value
-
specifies the shape parameter
 for fitted curves
requested with the BETA and GAMMA options.
Enclose the ALPHA= option in parentheses
after the BETA or GAMMA options.
If you do not specify a value for
for fitted curves
requested with the BETA and GAMMA options.
Enclose the ALPHA= option in parentheses
after the BETA or GAMMA options.
If you do not specify a value for  ,the procedure calculates a maximum likelihood estimate.
See Example 4.1.
You can specify A= as an alias for ALPHA= if you use it as a
beta-option.
You can specify SHAPE= as an alias for ALPHA= if you use it
as a gamma-option.
,the procedure calculates a maximum likelihood estimate.
See Example 4.1.
You can specify A= as an alias for ALPHA= if you use it as a
beta-option.
You can specify SHAPE= as an alias for ALPHA= if you use it
as a gamma-option.
- ALPHADELTA=value
-
specifies the change in successive estimates of
 at which iteration terminates in
the Newton-Raphson approximation of the maximum likelihood estimate
of
at which iteration terminates in
the Newton-Raphson approximation of the maximum likelihood estimate
of  for curves requested by the GAMMA option.
Enclose the ALPHADELTA= option in parentheses after the GAMMA option.
Iteration continues until the change in
for curves requested by the GAMMA option.
Enclose the ALPHADELTA= option in parentheses after the GAMMA option.
Iteration continues until the change in  is less than the value specified or until the number of
iterations exceeds the value of the
MAXITER= option.
The default value is 0.00001.
is less than the value specified or until the number of
iterations exceeds the value of the
MAXITER= option.
The default value is 0.00001.
- ALPHAINITIAL=value
-
specifies the initial value for
 in the Newton-Raphson
approximation of the maximum likelihood
estimate of
in the Newton-Raphson
approximation of the maximum likelihood
estimate of  for fitted gamma distributions
requested with the GAMMA option. Enclose the
ALPHAINITIAL= option in parentheses after the GAMMA option.
The default value is Thom's approximation of the estimate of
for fitted gamma distributions
requested with the GAMMA option. Enclose the
ALPHAINITIAL= option in parentheses after the GAMMA option.
The default value is Thom's approximation of the estimate of  .Refer to Johnson et al. (1994).
.Refer to Johnson et al. (1994).
- ANNOTATE=SAS-data-set
- ANNO=SAS-data-set
-
[Graphics]
specifies an input data set containing annotate variables
as described in SAS/GRAPH Software: Reference.
See Example 4.7.
The ANNOTATE= data set you specify
in the HISTOGRAM statement is used for all plots
created by the statement. You can also specify an
ANNOTATE= data set in the PROC CAPABILITY statement to
enhance all plots created by
the procedure; for more information, see
"ANNOTATE= Data Sets".
- BETA<(beta-options )>
-
displays a fitted beta density curve on the histogram.
The curve equation is

where  and
and
 lower threshold parameter (lower endpoint parameter)
lower threshold parameter (lower endpoint parameter)
 scale parameter
scale parameter 
 shape parameter
shape parameter 
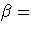 shape parameter
shape parameter  h = width of histogram interval
h = width of histogram interval
The beta distribution is bounded below by the parameter
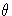 and above by the value
and above by the value  .You can specify
.You can specify 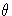 and
and  using the THETA=
and SIGMA= beta-options.
The following statements
fit a beta distribution bounded between 50 and 75,
using maximum likelihood estimates for
using the THETA=
and SIGMA= beta-options.
The following statements
fit a beta distribution bounded between 50 and 75,
using maximum likelihood estimates for  and
and
 :
:
proc capability;
histogram length / beta(theta=50 sigma=25);
run;
In general, the default values for
THETA= and SIGMA= are 0 and
1, respectively.
You can specify THETA=EST and SIGMA=EST to request
maximum likelihood estimates for 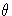 and
and
 .
.
The beta distribution has two shape
parameters,  and
and  . If these parameters
are known, you can specify their values with the ALPHA=
and BETA= beta-options. If you do not specify
values, the procedure calculates
maximum likelihood estimates for
. If these parameters
are known, you can specify their values with the ALPHA=
and BETA= beta-options. If you do not specify
values, the procedure calculates
maximum likelihood estimates for  and
and  .
.
The BETA option can appear only once in a HISTOGRAM
statement. Table 4.2 and Table 4.3
list options you can specify with
the BETA option. See Example 4.1.
Also see "Formulas for Fitted Curves".
- BETA=value
- B=value
-
specifies the second shape parameter
 for beta
density curves requested with the BETA option. Enclose
the BETA= option in parentheses after the BETA option. If you do
not specify a value for
for beta
density curves requested with the BETA option. Enclose
the BETA= option in parentheses after the BETA option. If you do
not specify a value for  , the procedure calculates
a maximum likelihood estimate.
See Example 4.1.
, the procedure calculates
a maximum likelihood estimate.
See Example 4.1.
- C=value
-
specifies the shape parameter c for Weibull density
curves requested with the WEIBULL option. Enclose the C= option
in parentheses after the WEIBULL option. If you do
not specify a value for c, the procedure calculates
a maximum likelihood estimate.
See Example 4.2.
You can specify the SHAPE= option as an alias for the C= option.
- C=value-list | MISE
-
specifies the standardized bandwidth parameter c
for kernel density estimates requested with the KERNEL
option. Enclose the C= option in parentheses after the
KERNEL option. You can specify up to five values to
request multiple estimates. You can also specify the
C=MISE option, which produces the estimate with a
bandwidth that minimizes the approximate mean
integrated square error (MISE). For example,
the following statements compute three density estimates:
proc capability;
histogram length / kernel(c=0.5 1.0 mise);
run;
The first two estimates have standardized
bandwidths of 0.5 and 1.0, respectively, and the third
has a bandwidth that minimizes
the approximate MISE.
You can also use the C= option with the K= option,
which specifies the kernel function, to compute multiple
estimates.
If you specify more kernel functions than
bandwidths, the last bandwidth in the
list is repeated for the remaining estimates. Likewise,
if you specify more bandwidths than kernel functions,
the last kernel function is repeated for
the remaining estimates. For example, the
following statements compute three density estimates:
proc capability;
histogram length / kernel(c=1 2 3 k=normal quadratic);
run;
The first uses a normal kernel and a bandwidth of 1,
the second uses a quadratic kernel and a bandwidth
of 2, and the third uses a quadratic
kernel and a bandwidth of 3.
See Example 4.5.
If you do not specify a value for c, the bandwidth
that minimizes the approximate MISE is used for all the
estimates.
- CAXIS=color
- CAXES=color
-
[Graphics]
specifies the color used for the axes and tick marks.
This option overrides any COLOR=
specifications in an AXIS statement. The default
is the first color in the device color list.
- CBARLINE=color
-
[Graphics]
specifies the color of the outline of histogram bars.
This option overrides the C= option in the
SYMBOL1 statement. The default is the first color
in the device color list.
- CDELTA=value
-
specifies the change in successive estimates of c
at which iterations terminate in the Newton-Raphson
approximation of the maximum likelihood estimate of
c for fitted Weibull curves requested by the
WEIBULL option. Enclose the CDELTA= option in parentheses after
the WEIBULL option. Iteration continues until the
change in c between consecutive steps is less than
the value specified or until the number of iterations exceeds
the value of the
MAXITER= option.
The default value is 0.00001. For examples, see the
entry for the WEIBULL option.
- CFILL=color
-
[Graphics]
specifies a color used to fill the bars of the histogram (or
the area under a fitted curve if you also specify the FILL option).
See the entries for the FILL and PFILL= options for additional
details.
See
Figure 4.5 and
Output 4.1.1.
Refer to
SAS/GRAPH Software: Reference for a list of colors.
By default, bars and curve areas are not filled.
- CFRAME=color
- CFR=color
-
[Graphics]
specifies the color for the area enclosed by the axes
and frame. The area is not filled by default.
- CHREF=color
- CH=color
-
[Graphics]
specifies the color for horizontal axis reference lines
requested by the HREF=option.
The default is the first color in the device color list.
- CINITIAL=value
-
specifies the initial value for
 in the Newton-Raphson
approximation of the maximum likelihood estimate of
c for Weibull curves requested with the WEIBULL option.
Enclose the CINITIAL= option in parentheses after the WEIBULL option.
The default value is 1.8 (refer to Johnson et al. 1994).
in the Newton-Raphson
approximation of the maximum likelihood estimate of
c for Weibull curves requested with the WEIBULL option.
Enclose the CINITIAL= option in parentheses after the WEIBULL option.
The default value is 1.8 (refer to Johnson et al. 1994).
- COLOR=color
-
[Graphics]
specifies the color of the density curve.
Enclose the COLOR= option in parentheses
after the distribution option or the KERNEL option.
See Example 4.1.
If you use the COLOR= option with the KERNEL option, you can specify a list of
up to five colors
in parentheses for multiple kernel density estimates.
If there are more estimates
than colors, the last color specified is used for the
remaining estimates.
- CTEXT=color
-
[Graphics]
specifies the color for tick mark values and axis labels.
The default is the color specified for the CTEXT= option
in the GOPTIONS statement.
In the absence of a GOPTIONS statement, the default color is
the first color in the device color list.
- CURVELEGEND=name | NONE
-
specifies the name of a LEGEND statement describing
the legend for specification limits and fitted curves.
Specifying CURVELEGEND=NONE suppresses the legend for
fitted curves; this is equivalent to specifying
the NOCURVELEGEND option.
- CVREF=color
- CV=color
-
[Graphics]
specifies the color for lines requested with the VREF= option.
The default is the first color in the device color list.
- DELTA=value
-
specifies the first shape parameter
 for
Johnson SB and Johnson SU
density curves requested with the SB and SU options. Enclose
the DELTA= option in parentheses after the SB or SU option. If you do
not specify a value for
for
Johnson SB and Johnson SU
density curves requested with the SB and SU options. Enclose
the DELTA= option in parentheses after the SB or SU option. If you do
not specify a value for  , the procedure calculates
an estimate.
, the procedure calculates
an estimate.
- DESCRIPTION='string'
- DES='string'
-
[Graphics]
specifies a description, up to 40 characters,
that appears in the PROC GREPLAY master menu. The
default is the variable name.
- EXPONENTIAL<(exponential-options )>
- EXP<(exponential-options )>
-
displays a fitted exponential density curve on the histogram.
The curve equation is

where
 threshold parameter
threshold parameter
 scale parameter
scale parameter  h = width of histogram interval
h = width of histogram interval
The parameter 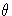 must be less than or equal to
the minimum data value. You can specify
must be less than or equal to
the minimum data value. You can specify 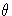 with
the THETA= exponential-option. The default value
for
with
the THETA= exponential-option. The default value
for 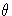 is zero.
If you specify THETA=EST, a maximum likelihood estimate
is computed for
is zero.
If you specify THETA=EST, a maximum likelihood estimate
is computed for 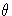 .You can specify
.You can specify  with the
SIGMA= exponential-option. By default, a maximum
likelihood estimate is computed for
with the
SIGMA= exponential-option. By default, a maximum
likelihood estimate is computed for  . For example,
the following statements fit an exponential curve with
. For example,
the following statements fit an exponential curve with
 and with a maximum likelihood estimate for
and with a maximum likelihood estimate for  :
:
proc capability;
histogram / exponential(theta=10 l=2 color=red);
run;
The curve is red and has a line type of 2.
The EXPONENTIAL option can appear only once in a
HISTOGRAM statement. Table 4.2 and
Table 4.4 list
options you can specify with the EXPONENTIAL option.
See "Formulas for Fitted Curves".
- FILL
-
[Graphics]
fills areas under a parametric density curve
or kernel density estimate with colors and patterns.
Enclose the FILL option in parentheses after a curve
option or the KERNEL option, as in the following statements:
proc capability;
histogram length / normal(fill) cfill=green pfill=solid;
run;
Depending on the area to be filled
(outside or between the specification limits),
you can specify the color and pattern with
options in the SPEC statement and HISTOGRAM statement,
as summarized in the following table:
|
Area Under Curve
|
Statement
|
Option
|
| between specification | HISTOGRAM | CFILL=color |
| limits | HISTOGRAM | PFILL=pattern |
| left of lower | SPEC | CLEFT=color |
| specification limit | SPEC | PLEFT=pattern |
| right of upper | SPEC | CRIGHT=color |
| specification limit | SPEC | PRIGHT=pattern |
If you do not display specification limits,
the CFILL= and PFILL= options specify the color and pattern
for the entire area under the curve.
Solid fills are used by default if patterns are not specified.
You can specify the FILL option with only one fitted curve.
For an example, see Output 4.1.1.
Refer to SAS/GRAPH Software: Reference for a list of
available patterns and colors.
If you do not specify the FILL option but specify the options in the
preceding table, the colors and patterns are applied to the
corresponding areas under the histogram.
- FITINTERVAL=value
-
specifies the value of z for the method of percentiles
when this method is used to fit a Johnson SB
or Johnson SU distribution.
The FITINTERVAL= option is specified in parentheses
after the SB or SU option.
The default value of z is 0.524.
- FITMETHOD=PERCENTILE|MLE|MOMENTS
-
specifies the method used to estimate the parameters
of a Johnson SB or Johnson SU distribution.
The FITMETHOD= option is specified in parentheses
after the SB or SU option.
By default, the method of percentiles is used.
- FITTOLERANCE=value
-
specifies the tolerance value for the ratio criterion
when the method of percentiles is used to
fit a Johnson SB
or Johnson SU distribution.
The FITTOLERANCE= option is specified in parentheses
after the SB or SU option.
The default value is 0.01.
- FONT=font
-
[Graphics]
specifies a software font for reference line and axis
labels. You can also specify fonts for axis labels in
an AXIS statement. The FONT= font takes precedence over
the FTEXT= font specified in the GOPTIONS
statement. Hardware characters are used by default.
- FORCEHIST
-
forces the creation of a histogram if there is only
one unique observation. By default, a histogram is not
created if the standard deviation of the data is zero.
- GAMMA<(gamma-options)>
-
displays a fitted gamma density curve on the histogram.
The curve equation is

where
 threshold parameter
threshold parameter
 scale parameter
scale parameter 
 shape parameter
shape parameter  h = width of histogram interval
h = width of histogram interval
The parameter 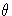 for the gamma distribution
must be less than the minimum data value. You can
specify
for the gamma distribution
must be less than the minimum data value. You can
specify 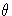 with the THETA= gamma-option.
The default value for
with the THETA= gamma-option.
The default value for 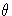 is 0.
If you specify THETA=EST, a maximum likelihood estimate
is computed for
is 0.
If you specify THETA=EST, a maximum likelihood estimate
is computed for 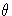 .In addition,
the gamma distribution has a shape parameter
.In addition,
the gamma distribution has a shape parameter  and a scale parameter
and a scale parameter  . You can specify these
parameters with the ALPHA= and SIGMA= gamma-options.
By default, maximum likelihood estimates are computed
for
. You can specify these
parameters with the ALPHA= and SIGMA= gamma-options.
By default, maximum likelihood estimates are computed
for  and
and  . For example, the following
statements fit a gamma curve with
. For example, the following
statements fit a gamma curve with  and with maximum
likelihood estimates for
and with maximum
likelihood estimates for  and
and  :
:
proc capability;
histogram length / gamma(theta=4);
run;
Note that the maximum likelihood estimate of  is calculated iteratively using the Newton-Raphson
approximation. The ALPHADELTA=,
ALPHAINITIAL=, and MAXITER= gamma-options control the
approximation.
is calculated iteratively using the Newton-Raphson
approximation. The ALPHADELTA=,
ALPHAINITIAL=, and MAXITER= gamma-options control the
approximation.
The GAMMA option can appear only once in a HISTOGRAM
statement. Table 4.2 and Table 4.5
list the options you can specify
with the GAMMA option.
See Example 4.2
and "Formulas for Fitted Curves".
- GAMMA=value
-
specifies the second shape parameter
 for
Johnson SB and Johnson SU
density curves requested with the SB and SU options. Enclose
the GAMMA= option in parentheses after the SB or SU option. If you do
not specify a value for
for
Johnson SB and Johnson SU
density curves requested with the SB and SU options. Enclose
the GAMMA= option in parentheses after the SB or SU option. If you do
not specify a value for  , the procedure calculates
an estimate.
, the procedure calculates
an estimate.
- HANGING
- HANG
-
requests a hanging histogram, as illustrated in
Figure 4.6.

and
lower threshold parameter (lower endpoint parameter)
scale parameter

shape parameter

shape parameter
h = width of histogram interval

threshold parameter
scale parameter
h = width of histogram interval

threshold parameter
scale parameter

shape parameter
h = width of histogram interval


threshold parameter
scale parameter
shape parameter
h = width of histogram interval

mean
standard deviation
h = width of histogram interval

threshold parameter

scale parameter

shape parameter
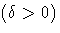
shape parameter
h = width of histogram interval
![p(x) = \{ \frac{ \delta h x 100\%}{\sigma \sqrt{2\pi} }
\frac{ 1 }
{ \sqrt{ 1 ...
...}{\sigma} )
)^2
]
& {for x \gt \theta } \ 0 & {for x \leq \theta\space }
.](images/hsteq41.gif)
location parameter

scale parameter

shape parameter
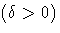
shape parameter
h = width of histogram interval

threshold parameter
scale parameter
c = shape parameter (c >0) h = width of histogram interval