Printed Output
If you request a fitted parametric distribution,
printed output summarizing the fit is produced
in addition to the graphical
display. Figure 4.9 shows the printed
output for a fitted lognormal distribution requested by
the following statements:
proc capability;
spec target=14 lsl=13.95 usl=14.05;
histogram / lognormal(indices midpercents);
run;
The summary is organized into the following parts:
- Parameters
- Chi-Square Goodness-of-Fit Test
- EDF Goodness-of-Fit Tests
- Specifications
- Indices Using the Fitted Curve
- Histogram Intervals
- Quantiles
These parts are described in the sections that follow.
Parameters
This section lists the parameters for the fitted curve
as well as the estimated mean and estimated standard
deviation. See "Formulas for Fitted Curves".
| The CAPABILITY Procedure |
| Fitted Lognormal Distribution for width |
| Parameters for Lognormal Distribution |
| Parameter |
Symbol |
Estimate |
| Threshold |
Theta |
0 |
| Scale |
Zeta |
2.638966 |
| Shape |
Sigma |
0.001497 |
| Mean |
|
13.99873 |
| Std Dev |
|
0.020952 |
| Goodness-of-Fit Tests for Lognormal Distribution |
| Test |
Statistic |
DF |
p Value |
| Kolmogorov-Smirnov |
D |
0.09148348 |
|
Pr > D |
>0.150 |
| Cramer-von Mises |
W-Sq |
0.05040427 |
|
Pr > W-Sq |
>0.500 |
| Anderson-Darling |
A-Sq |
0.33476355 |
|
Pr > A-Sq |
>0.500 |
| Chi-Square |
Chi-Sq |
2.87938822 |
3 |
Pr > Chi-Sq |
0.411 |
Capability Indices
Based on Lognormal
Distribution |
| Cp |
0.795463 |
| CPL |
0.776822 |
| CPU |
0.814021 |
| Cpk |
0.776822 |
| Cpm |
0.792237 |
Histogram Bin Percents
for Lognormal Distribution |
Bin
Midpoint |
Percent |
| Observed |
Estimated |
| 13.95 |
4.000 |
2.963 |
| 13.97 |
18.000 |
15.354 |
| 13.99 |
26.000 |
33.872 |
| 14.01 |
38.000 |
32.055 |
| 14.03 |
10.000 |
13.050 |
| 14.05 |
4.000 |
2.281 |
| Quantiles for Lognormal Distribution |
| Percent |
Quantile |
| Observed |
Estimated |
| 1.0 |
13.9440 |
13.9501 |
| 5.0 |
13.9656 |
13.9643 |
| 10.0 |
13.9710 |
13.9719 |
| 25.0 |
13.9860 |
13.9846 |
| 50.0 |
14.0018 |
13.9987 |
| 75.0 |
14.0129 |
14.0129 |
| 90.0 |
14.0218 |
14.0256 |
| 95.0 |
14.0241 |
14.0332 |
| 99.0 |
14.0470 |
14.0475 |
|
Figure 4.9: Sample Summary of Fitted Distribution
The chi-square goodness-of-fit statistic for a fitted
parametric distribution is computed as
follows:

where
Oi = observed percentage in i th histogram interval
Ei = expected percentage in i th histogram interval
m = number of histogram intervals
p = number of estimated parameters
The degrees of freedom for the chi-square test is
equal to m-p-1. You can save the observed and
expected interval percentages in the OUTFIT= data
set discussed in "Output Data Sets".
Note that
empty intervals are not combined, and the range of intervals used to
compute  begins with the first interval containing
observations and ends with the final interval
containing observations.
begins with the first interval containing
observations and ends with the final interval
containing observations.
When you fit a parametric distribution, the HISTOGRAM statement
provides a series of goodness-of-fit tests based on the empirical
distribution function (EDF). The EDF tests offer advantages over
the chi-square goodness-of-fit test, including improved power and
invariance with respect to the histogram midpoints. For a
thorough discussion, refer to D'Agostino and Stephens (1986).
The empirical distribution function is defined for a set
of n independent observations X1, ... ,Xn with a
common distribution function F(x). Denote the observations
ordered from smallest to largest as X(1), ... ,X(n).
The empirical distribution function, Fn(x), is defined as
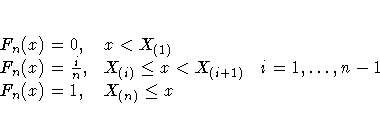
Note that Fn(x) is a step function that takes a
step of height [1/n] at each observation.
This function estimates the distribution function
F(x). At any value x, Fn(x) is the proportion
of observations less than or equal to x, while F(x)
is the probability of an observation less than or equal
to x. EDF statistics measure the discrepancy between
Fn(x) and F(x).
The computational formulas for the EDF statistics make
use of the probability integral transformation U=F(X).
If F(X) is the distribution function of X, the random
variable U is uniformly distributed between 0 and 1.
Given n observations X(1), ... ,X(n),
the values U(i)=F(X(i)) are computed by
applying the transformation, as shown in the
following sections.
The HISTOGRAM statement provides three EDF tests:
- Kolmogorov-Smirnov
- Anderson-Darling
- Cram
 r-von Mises
r-von Mises
These tests are based on
various measures of the discrepancy between the
empirical distribution function Fn(x) and the
proposed parametric cumulative distribution function F(x).
The following sections provide formal definitions of the
EDF statistics.
Kolmogorov-Smirnov Statistic
The Kolmogorov-Smirnov statistic (D) is defined as

The Kolmogorov-Smirnov statistic belongs to the
supremum class of EDF statistics.
This class of statistics is based on the
largest vertical difference between F(x) and Fn(x).
The Kolmogorov-Smirnov statistic is computed as the
maximum of D+ and D-, where D+ is the
largest vertical distance between the EDF and the
distribution function when the EDF is greater than
the distribution function, and D- is the largest
vertical distance when the EDF is less than the
distribution function.

Anderson-Darling Statistic
The Anderson-Darling statistic and the Cram r-von Mises
statistic belong to the quadratic class of EDF statistics.
This class of statistics is based on the squared difference
(Fn(x)- F(x))2. Quadratic statistics have
the following general form:
r-von Mises
statistic belong to the quadratic class of EDF statistics.
This class of statistics is based on the squared difference
(Fn(x)- F(x))2. Quadratic statistics have
the following general form:

The function  weights the squared difference
(Fn(x)- F(x))2.
weights the squared difference
(Fn(x)- F(x))2.
The Anderson-Darling statistic (A2) is defined as
![A^2 = n\int_{-\infty}^{+\infty}(F_n(x)-F(x))^2
[F(x)(1-F(x))]^{-1} dF(x)](images/hsteq85.gif)
Here the weight function is
![\psi(x) = [F(x)(1-F(x))]^{-1}](images/hsteq86.gif) .
.The Anderson-Darling statistic is computed as
![A^2 = -n-\frac{1}n\sum_{i=1}^n
[(2i-1)\log U_{(i)} + (2n+1-2i)
\log(\{1-U_{(i)})]](images/hsteq87.gif)
Cram r-von Mises Statistic
r-von Mises Statistic
The Cram r-von Mises statistic (W2) is defined as
r-von Mises statistic (W2) is defined as

Here the weight function is  .
.The Cram r-von Mises statistic is computed as
r-von Mises statistic is computed as

Probability Values for EDF Tests
Once the EDF test statistics are computed, the associated
probability values (p-values) must be calculated. The
CAPABILITY procedure uses internal tables of probability
levels similar to those given by D'Agostino and
Stephens (1986).
If the value is between two probability
levels, then linear interpolation is used to estimate the
probability value.
The probability value depends upon the parameters that
are known and the parameters that are estimated for the
distribution you are fitting. Table 4.17 summarizes
different combinations of estimated parameters for which EDF tests
are available.
Note: The threshold (THETA=) parameter for the beta,
exponential, gamma, lognormal, and Weibull distributions
is assumed to be known. If you do not specify its value,
it is assumed to be zero and known. Likewise, the SIGMA=
parameter, which determines the upper threshold (SIGMA)
for the beta distribution, is assumed to be known; if you
do not specify its value, it is assumed to be one. These
parameters are not listed in Table 4.17 because
they are assumed to be known in all cases, and they do not affect
which EDF statistics are computed.
Table 4.17: Availability of EDF Tests
|
Distribution
|
Parameters
|
EDF Tests Available
|
| Beta |  and and  unknown unknown | none |
| |  known, known,  unknown unknown | none |
| |  unknown, unknown,  known known | none |
| |  and and  known known | all |
| Exponential |  unknown unknown | all |
| |  known known | all |
| Gamma |  and and  unknown unknown | none |
| |  known, known,  unknown unknown | none |
| |  unknown, unknown,  known known | none |
| |  and and  known known | all |
| Lognormal |  and and  unknown unknown | all |
| |  known, known,  unknown unknown | A2 and W2 |
| |  unknown, unknown,  known known | A2 and W2 |
| |  and and  known known | all |
| Normal |  and and  unknown unknown | all |
| |  known, known,  unknown unknown | A2 and W2 |
| |  unknown, unknown,  known known | A2 and W2 |
| |  and and  known known | all |
| Weibull | c and  unknown unknown | A2 and W2 |
| | c known,  unknown unknown | A2 and W2 |
| | c unknown,  known known | A2 and W2 |
| | c and  known known | all |
Specifications
This section is included in the summary only if
you provide specification limits,
and it tabulates the limits as well as the
observed percentages and estimated percentages
outside the limits.
The estimated percentages are computed
only if fitted distributions are requested and are based on
the probability that an
observed value exceeds the specification limits,
assuming the fitted distribution. The
observed percentages are the percents of
observations outside the specification limits.
This section is included in the summary only if
you specify the INDICES option in parentheses after
a distribution option, as in the statements that produce Figure 4.9.
Standard process capability
indices, such as Cp and Cpk, are not
appropriate if the data are not normally distributed.
The INDICES option computes generalizations of the
standard indices using the fact that for the normal
distribution,  is both the distance from the
lower 0.135 percentile to the median (or mean) and the
distance from the median (or mean) to the upper 99.865
percentile. These percentiles are estimated from the
fitted distribution, and the appropriate
percentile-to-median distances are substituted for
is both the distance from the
lower 0.135 percentile to the median (or mean) and the
distance from the median (or mean) to the upper 99.865
percentile. These percentiles are estimated from the
fitted distribution, and the appropriate
percentile-to-median distances are substituted for
 in the standard formulas.
in the standard formulas.
Writing T for the target, LSL and USL
for the lower and upper specification limits, and
 for the
for the  percentile, the
generalized capability indices are as follows:
percentile, the
generalized capability indices are as follows:
-
Cpl = [(P0.5 - LSL )/(P0.5-P0.00135)]
-
Cpu = [(USL - P0.5 )/(P0.99865-P0.5)]
-
Cp = [(USL - LSL)/(P0.99865-P0.00135)]
-
Cpk = min([(P0.5 - LSL)/(P0.5-P0.00135)],[( USL - P0.5)/(P0.99865-P0.5)])
-
K = 2 ×[(|(1/2)( USL+ LSL) - P0.5|)/( USL - LSL )]

If the data are normally distributed, these formulas reduce
to the formulas for the standard capability indices, which
are given
at "Standard Capability Indices" .
The following guidelines apply to the use of
generalized capability indices requested with
the INDICES option:
-
When you choose the family of parametric distributions
for the fitted curve,
consider whether an appropriate family can be derived
from assumptions about the process.
-
Whenever possible,
examine the data distribution with
a histogram, probability plot, or quantile-quantile plot.
-
Apply
goodness-of-fit tests to
assess how well the parametric distribution models
the data.
-
Consider whether a
generalized index
has a meaningful practical interpretation in your application.
At the time of this writing, there is ongoing research concerning
the application of generalized capability indices, and it
is important to note that other approaches can be used with
nonnormal data:
-
Transform the data to normality, then compute and report
standard capability indices on the transformed scale.
-
Report the proportion
of nonconforming output
estimated from the fitted
distribution.
-
If it is not possible to adequately model the data distribution
with a parametric density,
smooth the data
distribution with a kernel density estimate
and simply report the proportion of nonconforming output.
Refer to Rodriguez (1992) for additional discussion.
Histogram Intervals
This section is included in the summary only
if you specify the MIDPERCENTS option in parentheses
after the distribution option, as in the statements that produce Figure 4.9.
This table lists the interval midpoints along with the
observed and estimated percentages of the observations
that lie in the interval. The estimated percentages
are based on the fitted distribution.
In addition, you can specify the MIDPERCENTS option
to request a table of interval
midpoints with the observed percent of observations
that lie in the interval. See the entry for the
MIDPERCENTS option.
Quantiles
This table lists observed and estimated quantiles. You can use
the PERCENTS= option to specify the list of quantiles to
appear in this list. The list in Figure 4.9
is the default list.
See the entry for the
PERCENTS= option.
Copyright © 1999 by SAS Institute Inc., Cary, NC, USA. All rights reserved.

![]() begins with the first interval containing
observations and ends with the final interval
containing observations.
begins with the first interval containing
observations and ends with the final interval
containing observations.
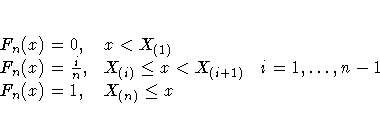



![A^2 = n\int_{-\infty}^{+\infty}(F_n(x)-F(x))^2
[F(x)(1-F(x))]^{-1} dF(x)](images/hsteq85.gif)
![A^2 = -n-\frac{1}n\sum_{i=1}^n
[(2i-1)\log U_{(i)} + (2n+1-2i)
\log(\{1-U_{(i)})]](images/hsteq87.gif)

![]() r-von Mises statistic is computed as
r-von Mises statistic is computed as

![]() for the
for the ![]() percentile, the
generalized capability indices are as follows:
percentile, the
generalized capability indices are as follows:
