NLPFDD Call
approximates derivatives by finite differences method
- CALL NLPFDD( f, g, h, "fun", x0, <,par,
"grd">);
See "Nonlinear Optimization and Related Subroutines" for a listing of all NLP subroutines.
See Chapter 11, "Nonlinear Optimization Examples," for a description of
the inputs to and outputs of all NLP subroutines.
The NLPFDD subroutine can be used for the following tasks:
- If the module "fun" returns a scalar, the
NLPFDD subroutine computes the function value
f, the gradient vector g, and the Hessian
matrix h, all evaluated at the point x0.
- If the module "fun" returns a column vector of m
function values, the subroutine assumes that a least-squares
function is specified, and it computes the function vector
f, the Jacobian matrix J, and the crossproduct
of the Jacobian matrix J'J at the point x0.
Note that in this case, you must set the first
element of the par argument to m.
If any of the results cannot be computed, the
subroutine returns a missing value for that result.
You can specify the following input
arguments with the NLPFDD subroutine:
- The "fun" argument refers to an IML module that returns
either a scalar value or a column vector of length m.
This module returns the value of the objective
function or, for least-squares problems, the values of
the m functions that comprise the objective function.
- The x0 argument is a vector of length
n that defines the point at which the
functions and derivatives should be computed.
- The par argument is a vector that
defines options and control parameters.
Note that the par argument in the NLPFDD call is
different from the one used in the optimization subroutines.
- The "grd" argument is optional and refers
to an IML module that returns a vector defining
the gradient of the function at x0.
If the "fun" argument returns a vector of values
instead of a scalar, the "grd" argument is ignored.
If the "fun" module returns a scalar,
the subroutine returns the following values:
- f is the value of the function at the point x0.
- g is a vector containing the value
of the gradient at the point x0.
If you specify the "grd" argument,
the gradient is computed from that module.
Otherwise, the approximate gradient is computed by
a finite difference approximation using calls of
the function module in a neighborhood of x0.
- h is a matrix containing a finite
difference approximation of the value
of the Hessian at the point x0.
If you specify the "grd" argument,
the Hessian is computed by calls of that
module in a neighborhood of x0.
Otherwise, it is computed by calls of the
function module in a neighborhood of x0.
If the "fun" module returns a vector,
the subroutine returns the following values:
- f is a vector containing the values
of the m functions comprising the
objective function at the point x0.
- g is the m×n Jacobian matrix J, which
contains the first-order derivatives of the functions
with respect to the parameters, evaluated at x0.
It is computed by finite difference
approximations in a neighborhood of x0.
- h is the n×n crossproduct of
the Jacobian matrix, JTJ.
It is computed by finite difference
approximations in a neighborhood of x0.
The par argument is a vector of length 3.
- par[1] corresponds to the opt[1]
argument in the optimization subroutines.
This argument is relevant only to least-squares
optimization methods, in which case it specifies the
number of functions returned by the module "fun".
If par[1] is missing or is
smaller than 1, it is set to 1.
- par[2] corresponds to the opt[8]
argument in the optimization subroutines.
It determines what type of approximation is to be used and
how the finite difference interval, h, is to be computed.
See "Finite Difference Approximations of Derivatives" for details.
- par[3] corresponds to the par[8]
argument in the optimization subroutines.
It specifies the number of accurate digits
in evaluating the objective function.
The default is
 ,
where
,
where  is the machine precision.
is the machine precision.
If you specify a missing value in the
par argument, the default value is used.
The NLPFDD subroutine is particularly useful for
checking your analytical derivative specifications of
the "grd", "hes", and "jac" modules.
You can compare the results of the modules with the finite
difference approximations of the derivatives of f
at the point x0 to verify your specifications.
In the unconstrained Rosenbrock problem (see
"Unconstrained Rosenbrock Function" ), the objective function is
-
f(x) = 50(x2-x12)2 + (1/2)(1-x1)2
Then the gradient and the Hessian,
evaluated at the point x=(2,7), are
![g^' & = & [ \frac{\partial f}{\partial x_1} \
\frac{\partial f}{\partial x_2}...
...2 - 200x_2 + 1 & -200x_1 \ -200x_1 & 100
]
= [ 1001 & -400 \
-400 & 100
]](images/i17eq206.gif)
The following statements define the Rosenbrock function and
use the NLPFDD call to compute the gradient and the Hessian.
They are shown in Figure 17.2.
proc iml;
start F_ROSEN(x);
y1 = 10. * (x[2] - x[1] * x[1]);
y2 = 1. - x[1];
f = .5 * (y1 * y1 + y2 * y2);
return(f);
finish F_ROSEN;
x = {2 7};
CALL NLPFDD(crit,grad,hess,"F_ROSEN",x);
print grad;
print hess;
GRAD
-1199 300.00001
HESS
1000.9998 -400.0018
-400.0018 99.999993
Figure 17.2: Finite Difference Approximations for Gradient and Hessian
If the Rosenbrock problem is considered from a
least-squares perspective, the two functions are
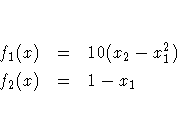
Then the Jacobian and the crossproduct of the
Jacobian, evaluated at the point x=(2,7), are
![J & = & [ \frac{\partial f_1}{\partial x_1} &
\frac{\partial f_1}{\partial x_2...
...& [ 400x_1^2+1 & -200x_1 \ -200x_1 & 100
]
= [ 1601 & -400 \
-400 & 100
]](images/i17eq208.gif)
The following statements define the Rosenbrock problem
in a least-squares framework and use the NLPFDD call
to compute the Jacobian and the crossproduct matrix.
Since the value of the PARMS variable, which is
used for the par argument, is 2, the NLPFDD
subroutine allocates memory for a least-squares
problem with two functions, f1(x) and f2(x).
The output is shown in Figure 17.3.
proc iml;
start F_ROSEN(x);
y = j(2,1,0.);
y[1] = 10. * (x[2] - x[1] * x[1]);
y[2] = 1. - x[1];
return(y);
finish F_ROSEN;
x = {2 7};
parms = 2;
CALL NLPFDD(fun,jac,crpj,"F_ROSEN",x,parms);
print jac;
print crpj;
JAC
-40 10
-1 0
CRPJ
1601 -400
-400 100
Figure 17.3: Finite Difference Approximations for Jacobian
Copyright © 1999 by SAS Institute Inc., Cary, NC, USA. All rights reserved.
![g^' & = & [ \frac{\partial f}{\partial x_1} \
\frac{\partial f}{\partial x_2}...
...2 - 200x_2 + 1 & -200x_1 \ -200x_1 & 100
]
= [ 1001 & -400 \
-400 & 100
]](images/i17eq206.gif)
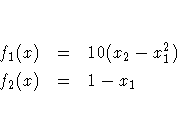
![J & = & [ \frac{\partial f_1}{\partial x_1} &
\frac{\partial f_1}{\partial x_2...
...& [ 400x_1^2+1 & -200x_1 \ -200x_1 & 100
]
= [ 1601 & -400 \
-400 & 100
]](images/i17eq208.gif)