Ryerson Crest Ryerson Header

MTH 207 Lab Lesson 22

Differential Equations

Up to Main Lab Page Previous Lesson - Numerical Integration

First Order Differential Equations

We have seen that finding the solution to a differential equation of the form

dy/dx = f (x),
y(x0) = y0.

is equivalent to finding int(f(t), t = x0 .. x);. Here f (x) is a known function and x0 and y0 are known numbers.

We have also seen that a differential equation of the form

dy/dx = ky,
y(x0) = y0.

has solution y(x) = A exp(kx), where the value of the constant A is determined by A = y0 exp(-kx0).

In general a first order differential equation consists of known numbers x0 and y0, and a known function of both x and y, f (x, y), such that

dy/dx = f (x, y),
y(x0) = y0.

The solution to such an equation involves finding a function, y(x) which satisfies both of these conditions.

The term "first order" refers to the fact that this equation only involves first order derivatives of the function y. There are also higher order differential equations but we will not consider them in this course.

A differential equation is an consists of two parts the dynamical condition, dy/dx = f (x, y), and the initial condition y(x0) = y0. If the initial condition is not given, we can still find the general solution to the equation, which will involve unknown constants.

An example of a first order differential equation would be

dy/dx = 2x - y,
y(0) = 1.

We would like to solve this by finding int(2x - y(x), x). However doing this integral involves finding the integral of y(x) with respect to x, to do this we must know y, but y is what we want to find in the first place!

Chapter 15 of Stewart deals with various analytical techniques for solving differential equations, however we will not be considering analytic solutions in this course.

dsolve

Maple has a function for solving simple differential equations dsolve The syntax is

dsolve( { <dynamical condition>, <initial condition> }, <var>)
<var> is the function which we are solving for, usually y(x).

So for example to silve the differential equation above we could try
dsolve({ diff(y(x), x) = 2*x - y, y(0) = 1}, y(x));

We can find the general solution by omitting the initial condition, in this case we don't need the braces '{'.
dsolve(diff(y(x), x) = 2*x - y, y(x));
 The constants are reported as C1, C2, etc. as needed. Note that a differential equation may have more than one solution.

  1. Use Maple to solve the following differential equations, where possible. In each case check the answer by differentiating.
    1. dy/dx = y2, y(0) = 1.
    2. dy/dx = y2 - x, y(0) = 1.
    3. dy/dx = y - x, y(0) = 1.
    4. dy/dx = 2y - x, y(0) = 1.
    5. dy/dx = sin(y), y(0) = 1.
    6. dy/dx = sin(y), y(0) = 0.
    7. dy/dx = sqrt(y), y(0) = 1.

Euler's Method

As with integrals there are many differential equations for which no closed form solution is known. Thus we must turn to a numerical method to find the solution.

In order to find a solution to a differential equation we must find a function y(x) which satisfies it. But y(x) is an analytical object, not a numerical one. Thus the best we can hope to do is to find a procedurre which will calculate the value of y(x) for some specific known value of x. We must repeat the method for each subsequent value of x. The method we will consider is known as Euler's method, after the Swiss mathematician Leonhard Euler (1707 - 1783) (Euler is pronounced 'oiler').

Thus we are given a first order differential equation.

dy/dx = f (x, y),
y(x0) = y0.

Where f (x, y) is a known function and x0 and y0 are known constants.

Euler's method relies on the fact that we know some things about the function y(x) near the point x0. In particular we know the value of the function there, y0, and the value of its derivative, f (x0, y0).

We are given x and we wish to find the value of y(x). We divide the interval from x0 to x into n equal intervals each of size h. As n gets larger, and hence h gets smaller, the accuracy of the method increases.

We will adopt the convention that
xk = x0 + k h.

Consider the linear approximation to y(x) about x0:
y(x) ~ y(x0) + y'(x0)(x - x0).
Thus y(x0 + h) ~ y(x0) + h y'(x0).

We now have the basis for an iterative method
y0 = x0
yk = yk-1 + h y'k-1.

We can estimate y'k-1 by y'k-1 = f (xk-1, yk-1).

So

y(x0 + kh) ~ yk = yk = yk-1 + h f (xk-1, yk-1).

This is the formula for Euler's method. The effect of this approximation is to follow the linear approximation to f till the next point, and then reevaluate, this is represented pictorially below.

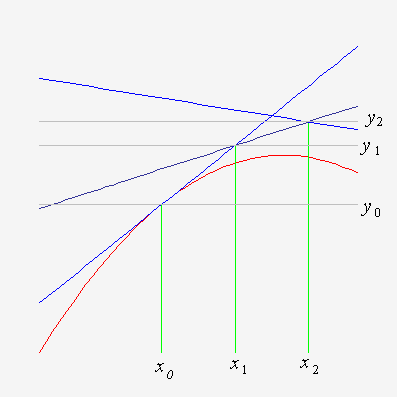
Effectively what we are doing is to approximate the slope of y between xk-1 and xk by the value of the slope at xk-1.

We can write a procedure to calculate the Euler approximation to a differential equation.
> eul:=proc(x,n, x0,y0,f)
> local h, y, z, k;h:=(x-x0)/n;
> y := y0;
> z := x0;
> for k from 1 to n
> do
> print(y, f(z,y));
> y := y + h*f(z,y);
> z := z+h;
> od;
> RETURN(y);
> end;
 Rem out the print statement (with #) to supress intermediate output.

The only thing we need now is to be able to define a function of two variables, f (x, y). We do this by putting both x and y in brackets before the ->.
> f := (x, y) -> -2*x - y;
> f(1, 2);

We can know try our method on a real example. Suppose we are given

dy/dx = 2x - y,
y(0) = 1.

Since this is an equation that Maple can solve we can check our answer against the true answer. We will try to use Euler's method to find y(0.5) using various values of n.
> dsolve({diff(y(x), x) = 2*x - y, y(0) = 1}, y(x));
> g := x -> (2*exp(x)*x - 2*exp(x) + 3)/exp(x);
> g(0.5);
> eul(0.5, 5, 0, 1, f); #h is 0.1
> eul(0.5, 10, 0, 1, f); #h is 0.05
> eul(0.5, 50, 0, 1, f); #h is 0.01

As we can see we need to do 50 iterations to get 2 digits accuracy.

  1. Use Euler's Method to to find y(1.5), where y is the solution to the following differential equations, where possible check the answers against Maple's dsolve.
    1. dy/dx = y2 - x, y(0) = 1.
    2. dy/dx = 2y - x, y(0) = 1.
    3. dy/dx = sin(y), y(0) = 0.
    4. dy/dx = sqrt(y), y(0) = 1.
    5. dy/dx = exp(y), y(0) = 1.
    6. dy/dx = sqrt(y) - x, y(0) = 1.
    7. dy/dx = y3 - x, y(0) = 1.

Modified Euler's Method

The main problem with Euler's method is that it is not very accurate. We need a large number of iterations to get a reasonable degree of accuracy. The reason for this is that the method estimates the slope over the interval [xk-1, xk] from the slope at xk-1. A better estimate would be to use the average of the slopes at the endpoints (y'k + y'k-1)/2. The trouble with this is that we don't know y'k until after we have calculated yk.

What we do is use the estimate from Euler's method, yk,p, to estimate y'k = f (xk, yk,p), we then use this to calculate (y'k + y'k-1)/2.

The modified Euler method is what is known as a predictor - corrector method. We have a predicted value from Euler's method, yk,p, the predictor. We use this to calculate a corrected value for yk, yk,c the corrected value.

yk,c = yk-1 + h (y'k + y'k-1)/2.
where y'k = f (xk, yk,p).
yk,p = yk-1 + h f (xk-1, yk-1).

Of course we may repeat the predictor corrector step as many time as we want to get better estimates. Each time we get a corrected value we use it for the predictor of the next iteration. Usually we continue until the difference between the predicted value and the corrected value is less than some preasssigned value.

We can now implement the algorithm.
meul := proc(x, n, x0, y0, f)
local h, y, z, k, yp, yc, check;
h := (x - x0)/n;
y := y0;
z := x0;
for k from 1 to n do
print(`yk = `, y, `h yk' = `, h*f(z,y));
yp := y + h*f(z, y);
check := abs(yp+1);
while evalf(check) > evalf(10^(-2)) do
yc := y + h*(f(z, y) + f(z+h, yp))/2;
print(`yp = `, yp, `h dy = `, h*f(z+h, yp), `h dyav = `, h*(f(z, y) + f(z+h, yp))/2, `yc = `, yc);
check := abs(yp - yc);
#corrector is predictor for the next round
yp := yc;
od;
y := yc;
z := z+h;
od;
RETURN(y);
end;
Rem out the print statements (with #) to reduce the output.

We can know try our method on a real example. Suppose we are given

dy/dx = 2x - y,
y(0) = 1.

Since this is an equation that Maple can solve we can check our answer against Maple's answer, 0.819591979137900270811398604978. We will try to use Euler's method to find y(0.5) using various values of n.
> Digits := 30;
> meul(0.5, 5, 0, 1, f); #h is 0.1
> meul(0.5, 10, 0, 1, f); #h is 0.05
> meul(0.5, 50, 0, 1, f); #h is 0.01

  1. Use the modified Euler's Method to find y(1.5), where y is the solution to the following differential equations, where possible check the answers against Maple's dsolve.
    1. dy/dx = y2 - x, y(0) = 1.
    2. dy/dx = 2y - x, y(0) = 1.
    3. dy/dx = sin(y), y(0) = 0.
    4. dy/dx = sqrt(y), y(0) = 1.
    5. dy/dx = exp(y), y(0) = 1.
    6. dy/dx = sqrt(y) - x, y(0) = 1.
    7. dy/dx = y3 - x, y(0) = 1.

Up to Main Lab Page Previous Lesson - Numerical Integration Top of this Lesson

Maintained by: P. Danziger, April 1998