Ryerson Crest Ryerson Header

MTH 207 Lab Lesson 14

Newton's Method

Up to Main Lab Page Next Lesson - Fixed Point Iteration Previous Lesson - The Bisection Method

Newton's Method

[See section 2.10 of Stewart]

The bisection method is useful only up to a point. In order to get good accuracy we must do a relatively large number of iterations. This is even more of a problem if many roots are to be found. A much better algorithm is Newton's method.

The idea of Newton's method is to make an initial guess, a0, close to the root.
The point where the tangent line to f at a0 meets the x axis is our next approximation, a1.
We then repeat as needed.

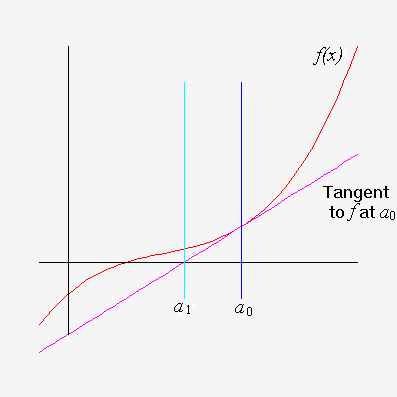
We can calculate the value of the n+1th step in this process, an+1, from an, f (an) and f '(an).
The equation of the tangent at an is
y = f '(an)(x - an) + f (an).
Expanding gives
y = x f '(an) - an f '(an) + f (an).
an+1 is the point where this line crosses the x axis. This happens when y = 0, solving y = 0 gives:

an+1 = an - f (an) / f '(an).

This is the formula for the next approximation in Newton's Method.

The Algorithm

Pick a starting value for a.
Repeat
a := a - f (a) / f '(a)
Return a

Methodological Error

The Methodological Error for Newton's method is fairly hard to prove and involves the second derivative of the function f.
En+1 = ½ g''(u) En2
where u is some point between the real root and the approximation and g(x) = x - f (x)/f '(x).
This shows that in Newton's method the error decreases quadratically, rather than linearly as with the Bisection method (En+1 = ½ En).

Unfortunately this error bound is not much use for practical purposes. A much more useful way of estimating the error is that it can be shown that the difference between successive approximations is greater than the error. Thus
En+1 < |an+1 - an|
Note that |an+1 - an| = |f (an) / f '(an)|

Thus we may continue iterating until the difference between successive approximations, |an+1 - an|, is less than the required value.

Example

Again we will attempt to solve the equation cos2(x) = x.
Once again we first put this equation in the form f (x) = 0, by putting f (x) = cos2(x) - x.
> f := x -> cos(x)^2 - x;

We will need the derivative of f.
> g := D(f);

We need a first approximation for a0. We get this by looking at a plot.
> plot(f(x), x = -Pi..Pi);

We once again see that the root is between 0 and 1, thus 0.5 would be a reasonable assumption for a0.
> a := .5;

We will again set the error to 10-20, and ensure that the accuracy is high enough.
> error := 10^(-20);
> Digits := 30;

We now implement the algorithm. We use the variable b to record the error at each stage, we initially set this to 1.
> b := 1;
> while abs(evalf(b)) > error
> do
> b := f(a)/g(a);
> a := a - b;
> od:

We can now see the answer.
> a;

We can check that this agrees to the answer given by the Bisection method to within 20 decimal places.
> evalf(a - 0.6417143708728826583998394901542372537051);

  1. The above algorithm uses a seperate variable g for the derivative, which is calcuated outside the loop, why is this a good idea?
    Why do we use the variable b?
  2. Rewrite the algorithm for Newton's method to include a counter, which counts the number of iterations through the loop.
    1. How many iterations did the calculation above take?
    2. Compare this result with that for the Bisection method. Which would you say is the better method?
    3. If error is set to 10-10, guess how many iterations will be needed. Why is this now a hard question?
      Use your program to find the answer.
  3. Use Newton's method to estimate a roots of the following to within 10-10. In each case record the number of iterations needed. Compare your answer to the number needed for the Bisection method.
    1. x^6 + x^4 - 3*x^5 + 5*x^3 - 6*x^2 + 2*x - 1 (both roots).
    2. tan(x) = 2x (principal root).
    3. e^x = 3x.
    4. sin(x) - x^2 has a root at x = 0, find the other root.
  4. Use Newton's method to estimate the following quaintities to 20 decimal places by solving a relavent equation. (The equation may be given in parenthasise.)
    1. Pi/2.
    2. Pi.
    3. sqrt(2) (Use x^2 - 2).
    4. The sixth root of 2.
    5. e

Problems With Newton's Method

While the convergence of Newton's method is very good (5 iterations in the above example, compared to 67 for Bisection), it does have certain potential problems associated with it.

First if f '(x) = 0 near the root, then both the numerator and denominator in f (an) / f '(an) are near zero. This necessitates a computation of both f (an) and f '(an) to a high degree of accuracy.

Further we must be careful to avoid points for which f '(an) = 0, since this will produce a divide by 0 error. This is particularly important in our first guess.
In a similar vien we must avoid points where the derivative is undefined.

If any of our an are close to a turning point of f the tangent will be nearly flat and the intercept will be far away.

If our initial guess is on the other side of a turning point of f, where there is no root it is possible that the method will diverge, or at least converge very slowly.

As an example consider the following picture showing successive approximations from an initial "bad" guess.

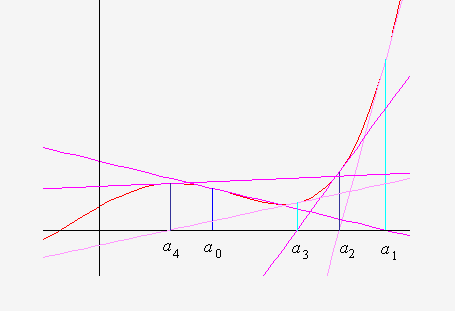
a0 is on the wrong side of the turning point, and so a1 is further away from the root.
a2, a3 and a4 are once again moving closer to the root.
Though a4 is on the right side of the turning point it is close to the turning point and so the tangent is nearly flat, thus the intercept will be far away from the root.

Finally there is a possibility that the algorithm does not converge at all, but bounces between two values.
To see this consider the picture below.

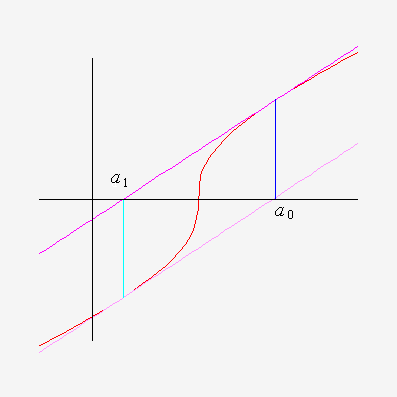
The tangent to a1 hits the axis at a0, thus a2 = a0
Continuing, the tangent of a2 is the same as the tangent to a0, and so a3 = a1.
In general
an = a0 If n is even
a1 If n is odd

Thus the iteration jumps forever between these two values and never converges to the root.

  1. The function f(x) = x^5 + 3*x^4 - 9*x^3 - 23*x^2 + 24*x + 36 has a root at x = 2.
    1. Plot f(x).
    2. Try to find this root using Newton's Method, starting with a = 1. What goes wrong, why?
    3. Try Using a = 0.5 to an accuracy of 10-20. How many iterations did it take? Why so many?
    4. Using a = 1.5 should be better, as it is closer to the root, and avoids the turning point near .5.
      Try using a = 1.5 to an accuracy of 10-20.
      How many iterations did it take? Why so many?
    5. To see that this is a property of the root, rather than the function try to find the root at -1, using a suitable guess for a0.
  2. Let
    f(x) = -sqrt(4 - x) If x < 4
    sqrt(x - 4) If x >= 4
    Clearly f(x) has a root at x = 4.
    1. Plot f(x).
    2. Try using Newton's method to an acuracy of 10-5 starting at any point of your choosing, outside of the range [4 - 10-5, 4 + 10-5].
      Note, you may find the STOP button on the tool bar useful at this point. You also may want to issue a restart to clear the memory.
      Try some other points.
    3. Investigate a few iterations of the method to see what went wrong.
    4. Use Maple to find the value of f(x)/f'(x) and x - f(x)/f'(x), simplify your answers as much as possible.
      Can you now explain this behaviour?

    Up to Main Lab Page Next Lesson - Fixed Point Iteration Previous Lesson - The Bisection Method Top of this Lesson

    Maintained by: P. Danziger, Febuary 1998