MAT 335 Weekly Summary Part I: Fractals
Winter, 2003
Page numbers refer to the text.
Also look at the previous year's commentary; W2000,
W2001, and W2002.
Some useful formulae
Last updated: 11 Feb
Click on the date to go to that section: 6 Jan. (Cantor set),
13 Jan. (Self-similarity of the Cantor set, Sierpinski's Triangle, von Koch curves, measuring
lengths of curves), 20 Jan. (Fractal dimension, box counting method, drawing
fractals: IFS), 27 Jan. (IFS, Contraction Mapping Principle, Hausdorff Distance),
3 Feb.(Decoding an IFS, Fractal Image Compression, Chaos Game), 10 Feb.
(Chaos Game; Game 'Rules', adjusting probabilities).
Summary for Dynamics
(Week of) 6 January
The Cantor set (pp 67-72, 75-77). The Cantor set C can be constructed by removing the (open)
middle third
from [0,1] and then removing the middle thirds from the remaining intervals [0,1/3], [2/3,1], etc ad infinitum.
The Cantor set is the set of points remaining. By adding up
the lengths of the intervals removed (using the formula for a geometric series)
we see that the "length" of C must be zero (because the lengths of all the intervals removed in the
construction is 1).
Although the length of C is zero, there are many points in C. For instance, it's easy to see
that the end points E = {0, 1, 1/3, 2/3, 1/9, 2/9, 7/9, 8/9, . . . } of the intervals removed are in
C. But there are many, many more points in C (for example, 1/4 and 3/4 are in C).
To find out exactly what points are in C, it is best to look at the
ternary (or triadic) expansions of numbers in [0,1].
This way we see that the points in C have
no 1 in their ternary expansion (since those regions of [0,1] containing numbers with a 1 in their
ternary expansion were removed in the construction of C). Conversely, any number in [0,1]
that has no 1 in its ternary expansion is in C. For those numbers that have two ternary
expansions, if one of them has no 1 then that number is in C (for example, [1/3]3
= .1 or .022(22) ). It is important to note that any string .a1a2
a3. . . of 0's and 2's corresponds to (the ternary expansion of)
a number in C.
Now we "match" the numbers in [0,1] to the numbers in C, in a one-to-one manner, to show that
C contains at least as many points as [0,1]. To do that we first express numbers in [0,1] in base
2, i.e., we look at their binary expansions. So take any x in [0,1] and let
[x]2 = .b1b2b3. . . be its binary expansion.
Now we change every 1 that occurs in the binary expansion of x to a 2.
Then we are left with a string .c1c2c3. . . of 0's and
2's (the c's that are 0 are in the same position as the 0's in the binary
expansion of x). So this string must correspond to a (unique) number y in C where
[y]3=.c1c2c3. . . .(because of the important note
in the previous paragraph). Thus, we have matched every x in [0,1] to a (different) y in C and so
the cardinality of [0,1] and C must be equal
(i.e., the number of points in [0,1] and C must be the same).
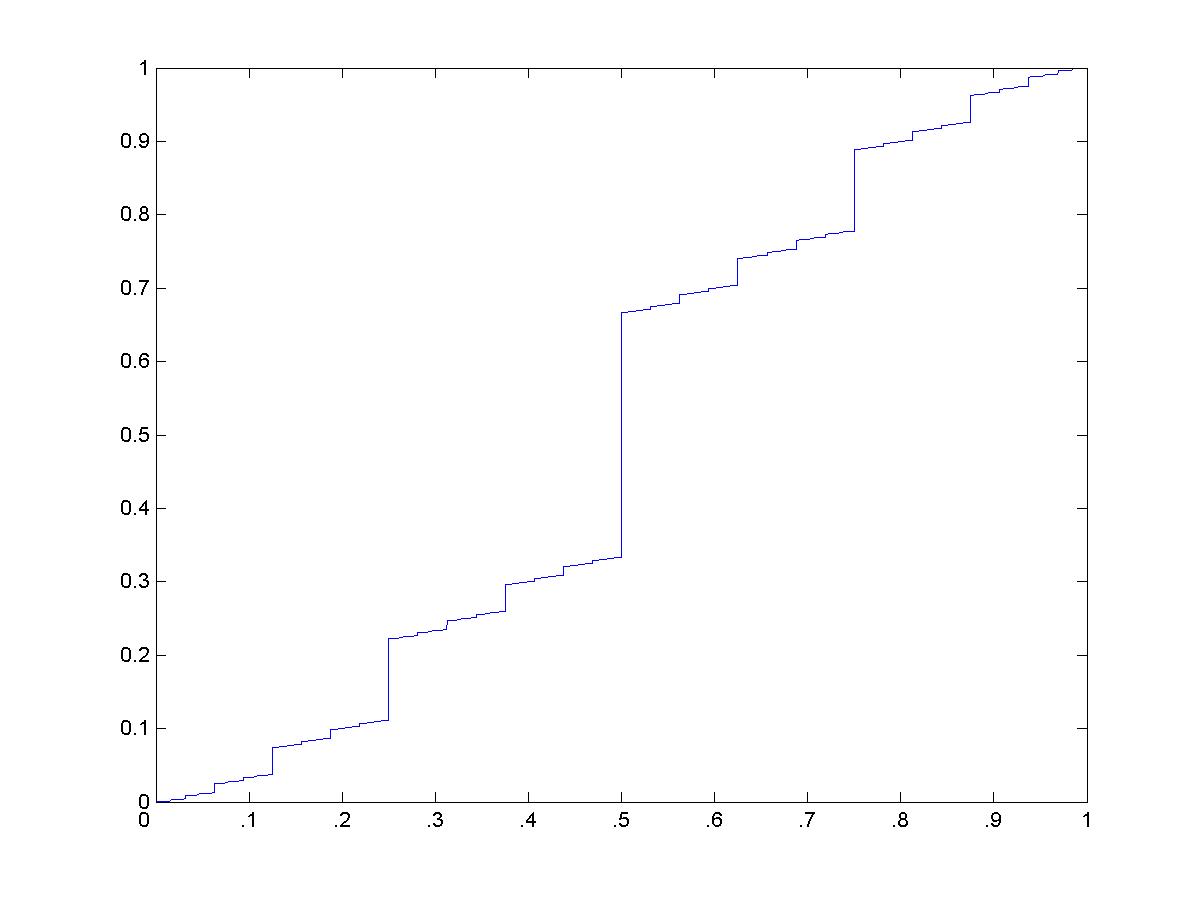
The graph of the function g: [0,1] to C via [x]2 goes to y in C
by changing every '1' in [x]2 to a '2' to obtain [y]3; see page 75 in
the text. Compare this to the 'Devil's Staircase', Figure 4.39 on page 226.(Click
here
for a larger view.) The MATLAB program that calculated this is
here.
Properties of C;
- the length of C is zero
- C contains no intervals, i.e., is it "dust" ('totally disconnected' in mathematical jargon). Thus,
between any two points in C is a point that is not in C.
- C has the same cardinality as [0,1]
- C is self-similar (i.e., small pieces of C are exact replicas - albeit on a smaller scale - of
C)
- every point x in C is the limit of a sequence of end points. That is, there is an (infinite) sequence
{yi} of points from E such that yi tends to x as i tends to infinity. So the end
points "cluster" around the points in C.
13 January
Self-similarity (Chapter 3; pp 135-146). Here's a formal definition;
A set S in Rn is self-similar (or affinely self-similar) if there is a subset
s of S, an (n by n) matrix A (or linear transformation) that is expanding, and a
vector v in Rn, such that
A(s) + v = S.
(A linear transformation A is expanding if ||A(x)-A(y)|| is
greater than ||x-y|| for all x,y in Rn.)
That is, a set is self-similar if a small piece of it is an
exact replica of the entire whole (after expanding it and shifting it if necessary).
This implies that the set is infinitely complicated; the small piece, being a replica of the whole,
itself has a smaller piece which is a replica of the whole small piece, etc. We proved the
self-similarity of the Cantor set using ternary expansions, and noted the self-similarity of
the Sierpinski triangle and von Koch curve. Every fractal has this self-similarity (although
sometimes it is not so obvious - for example, the fractal tree
(also shown on page 242 of the text)). And, as we will see, many 'real' objects have some
self-similarity.
Some notes on using ternary expansions to prove the self-similarity of the Cantor set
can be seen here; self_cantor.pdf,
or self_cantor.jpg.
We started discussing the Sierpinski triangle (pp 78-79).
We discussed the von Koch curves (pp 89-93).
The Sierpinski triangle (pp 78,79) and the von Koch curve (pp 89-93, 147-152). Both were obtained
by a recursive algorithm. The Sierpinski triangle contains an infinitely long curve (the edges of
the triangles removed) and the von Koch curve is infinitely long. The von Koch curve intersects
the interval [0,1] at exactly the Cantor set, and at each end point E of the intervals removed in the
Cantor set construction (as described above) there is a corner of the von Koch curve. Keep in mind that the von
Koch curve is a continuous curve and that the Cantor set is dust! So the von Koch curve is
oscillating wildly (to put in mildly) along the interval [0,1]. That's what you need to do
to fit an infinitely long curve into an area of finite size!
Measuring the complexity of curves (Section 4.2). Here we are after the exponent d
in the relation log[u(s)] vs log(1/s). Here, u(s) is the length of
the curve measured with rulers of size s (so if N(s) rulers of length s are
needed to measure the length of the curve, u(s) = N(s)*s). We sometimes say that "u(s)
is the length of the line at scale s".
The exponent d
is the slope of the (straight line part) of the curve that passes through the points when you
plot log[u(s)] against log(1/s) (see Figures 4.12, 4.18 and 4.20 in the
text). Note that if the data points (log[u(s)], log(1/s)) lie on a straight line of
slope d, then log[u(s)] = d*log(1/s) + b, so (taking the exponential of both
sides of this equation) u(s) = k*(1/s)d (here, k = eb).
That is, u(s) is proportional
to (1/s)d.
We saw that 'regular' curves have exponent d=0 and that 'fractal-like' curves
have positive exponent; d>0. If d=0 then the length of the curve increases at the
same rate at which the ruler used to measure the length shrinks (eg. if I shrink the size of
the ruler by 3 (so it becomes 1/3 its previous length), the number of rulers needed to measure the
length of the curve
goes up by a factor of 3 too, etc). However, if d>0 then the number of rulers needed to measure the
length of the curve increases at
a faster rate than the rate at which the scale s is shrinking (for example,
with the von Koch curve, if you shrink the scale by a factor of 3, the number of rulers
you need goes up by a factor of 4). You can see this from the formula
u(s) = c(1/s)d - so if you shrink the ruler from size s to size
s/m, then the length of the line at this smaller scale is u(s/m) =
c(1/(s/m))d = mdc(1/s)d = mdu(s); the
length increases by a factor of md (here we are thinking of m >1).
See also last year's commentary; 14 January and
21 January.
January 20
Fractal Dimension (or self-similarity dimension) (Section 4.3).
Here we are measuring the complexity of sets by covering them with small squares or cubes
and counting how many of these small squares or cubes are needed to cover the set. We then
shrink the size of these small squares or cubes and count again how many of these smaller
squares and cubes are needed to cover the set. Of course, since the squares or cubes are
shrinking in size we will need more of them to cover the set, but for some sets the increase
in the number of small squares or cubes is greater than for other sets. The rate of increase in the
number of small squares or cubes need to cover the set as they shrink in size is a measure of the
complexity of the set; as our scale decreases in size we see the same or even more detail
in complicated sets than for less complicated sets (i.e., 'regular' sets).
As for the length of curves, we expect a power law relation between the number of small
squares or cubes needed to cover the set, a(s), and the size (or scale) if the
small squares or cubes, s. That is, we expect a formula of the type
u(s) = c(1/s)D for some D > = 0 (D will be greater or
equal to zero since the number of small squares or cubes needed to cover the set increases
as the scale shrinks). The exponent D is called the fractal dimension of the set.
To compute the fractal dimension of a set, you choose an (appropriate) sequence of scales sn
such that sn -> 0 as n -> infinity,
and count the minimum number of squares or cubes a(sn) that are needed
to cover the set. Then you write a(sn) as a power law;
u(sn) = c(1/sn)D for some constant c
. The exponent D you find is the
fractal dimension of the set. Note that we would just write u(s) = c(1/s)D;
that is, just s instead of sn.
It's easy to calculate the fractal dimension of simple sets. For a line segment of length L
we choose the scales sn = L/n, n=1, 2, 3, ... and cover it with line
segments or squares or cubes of size sn. Here, a(sn) = n.
We can write n = L/n = L(1/sn)1 so that a(s) = L(1/s)1
and so we see that the fractal dimension for a line is 1. For a square of size L we
choose the same scales sn = L/n and cover the square with small squares or
cubes of size sn. Here, a(sn) = n2 =
L2(1/sn)2 so the fractal dimension of a square
is 2. For a cube we find that a(sn) = n3 = L3
(1/sn)3 so the fractal dimension of a cube is 3. With a bit of
help from calculus, we would find that the fractal dimension of any regular curve is 1,
the fractal dimensio of any regular area is 2, and that the fractal dimension of any
regular volume is 3. Thus, for regular sets the fractal dimension agrees with the
topological dimension.
However, the topological dimension doesn't say anything about the complexity
of a set, and that's what we are trying to study here (and what scientists in general
are studying when they study fractals and chaos). For example, the von Koch curve,
the Sierpinski triangle, and Peano's space filling curve (see pp 94) are all curves (i.e.,
they have topological dimension 1), but they are not anything like 'regular' curves
because they are infinitely complicated; when you zoom in on them they look the same.
Their complexity is reflected in their fractal dimensions; D = 1.26, 1.58, and 2 for
the von Koch, Sierpinski and Peano curves respectively - von Koch is the least
complicated of the three (but still infinitely more complicated than a regular curve),
Sierpinski is the next most complicated, and the Peano curve is the most complicated
of the three. In fact, the Peano 'curve' is more like an area than a line.
To get a better idea of what the fractal dimension is telling us about a set, let's consider the unit
square [0,1]2 and the grids of size sn = (1/2)n that cover
the square (the top part of Figure 4.30, pp 213, shows two grids; see also the examples
given below). If A is any subset of
[0,1]2, then to calculate the fractal dimension of A we cover it with grids of various
sizes and count how many of the small squares of each grid (the minimum number) are needed to cover A.
Then we calculate the exponent D as described above. But let's go backwards and start with the
covering rather than with the set (let's remark that a covering at scale sn is just a selection
of small squares from the grid of size sn). A consistent covering is a selection
of covers from each grid size in such a way that
in the covering at any scale only the small squares that are within the squares choosen for the
covering at the previous step can be used. If you think about it, for any choice of consistent covering
there is a set A that has that covering.
Doing this allows us, for one thing, to find a set A
with prescribed fractal dimension. For example, if we wanted to find a set with fractal dimension
(log 3)/(log 2) = 1.58, we would just choose a covering that had a(sn) = 3n
squares at scale sn (because a(sn) = 3n = (1/sn)
D = (2n)D for D = (log 3)/(log 2).) An important observation is that
the fractal dimension only depends on the number a(sn) of squares choosen at
each scale and not on their arrangement. This implies that you can find many sets with
the same fractal dimension; just choose the a(sn) squares differently (but consistently!)
when making a new covering. You can also get an idea of what the set A looks like that has that
fractal dimension by sketching the coverings at smaller and smaller scales.
As an example, for each scale sn choose the 2n diagonal squares in the
grid. This is a consistent covering and you can see that the set A = diagonal line has this
covering. Since a(sn) = 2n = (1/sn)1, A has
fractal dimension 1 (which we knew already). But we can rearrange the 2n squares at
each scale in a consistent way to obtain the covering of another set B that also has fractal
dimension 1. In fact, you can choose the covering so that B is not a line at all but in fact
is dust!
Here are two examples of consistent coverings:
one with fractal dimension 1; JPEG format,
PDF format,
and one with fractal
dimension 1.5;
JPEG format, and PDF format
. See
here for a larger picture of the fractal set covered by the latter covering.
Another thing we can do here is try to get some idea of how much you can vary a covering without changing
the fractal dimension. For example, suppose a1(sn) is the number of grid
squares used at scale sn for a covering that gives fractal dimension D1.
Suppose at each scale sn we remove k of the squares of that covering. Then we can
conclude that no matter how large k is the fractal dimension of the resulting covering is
still D1 (note that you could not begin removing the k squares until you reached a
small enough scale m so that a1(sm) > k). We prove this in the case when
the covering is for the entire square [0,1]2, so a1(sn) = 4n:
We start removing squares from the the original covering at some stage m where
k < a1(sm) = 4m.
Let a(s) denote the number of squares used at scale s in our new covering.
Then
a(sm) = 4m - k (so there are 4(4m - k) = 4m+1 - 4k
squares of size sm+1),
a(sm+1) = 4m+1 - 4k - k (so there are 4(4m+1 - 4k -k) squares
of size sm+2),
...
...
...
a(sm+p) = 4n - k(4p + 4p-1 + . . . + 4 + 1) =
4n - k(4p+1-1/3), (n = m+p).
So log a(sn) = log[ 4n - k(4p+1-1/3)]
= log 4n - log[(4n - k(4p+1-1/3)) / 4n]. Now, as
i tends to infinity, (4n - k(4p+1-1/3))/ 4n tends to 1 (note that
p+1 = n-m+1). Thus, log s(sn) -> log 4n as n tends to
infinity, and so the fractal dimension of our new covering remains 1.
In practice, the fractal dimension of a set is often measured by the box counting method. See the
Jan 21 commentary, W00 for discussion of this, and Section 4.4 of the text.
In practice, the fractal dimension of a set is often estimated by
the box counting method (Section 4.4, pp 212-216; see also
the 21 Jan 2000 commentary).
We started on Iterated Function Systems (IFS). To motivate this we considered the Multiple
Reduction Copy Machine (MRCM) paradigm (see Sections 1.2 and 5.1 and the
28 Jan, 2000 commentary). This is a kind of photocopier that has
several lenses, each one reduces the size of the object it images, and then the resulting images
are arranged in some particular way on the resulting output. For example, the Sierpinski MCRM has
three lenses, each one reduces to 1/2 size, and the resulting three images are arranged at the
vertices of an equilateral triangle (see Figure 1.9). If you you feed the resulting image back into the
MCRM over and over again, the output begins to look like the Sierpinski triangle (see Figures 1.10 and
5.1). In fact, all fractals can be obtained this way.
What characterizes an MCRM (and an IFS) is its blueprint (see page 238). The blueprint is
simply the image of the unit square by the MCRM. For the Sierpinski MCRM the blueprint
consistes of three squares of size 1/2 arranged in an equilateral triangle (see Figure 5.9, for
example). If we indicate the orientation of the square by placing an 'L' in the top left
corner, then the blueprint tells us everything about the MCRM (and IFS); how many lenses are
involved, what each lens does (eg., shrink, rotation, reflection, etc.), and how the images
produced by each lens are arranged in the output. It's important to note that the fractal
produced by an MCRM (or IFS) is unchanged when imaged by that MCRM. This is really the
only way to determine what kind of image is produced by an MCRM or IFS (we will discuss this
more later).
Each lens of an MRCM is modelled mathematically by an affine transformation w which is
a transformation of the form w = A + v where A is a (2 by 2) matrix and v
is a vector (in R2). For most purposes, the matrices A can be realized
as a composition of 'elementary' transformations like rotations, reflections, dilations (in
both x and y directions), and shears (see page 234-236). The mathematical model
of the MCRM is, then, an IFS W; W = w1 U w2 U . . .
U wk where each wi=Ai+vi
is an affine transformation (the matrices Ai and vectors vi
may differ for each lens).
See Ch 5 and Section 3.4; and 28 January W00 commentary, and
2 Feb W01 commentary.
See here for examples of iterates of various IFS.
(Week of) 27 January
We looked at the problem of encoding an image as an IFS (Chapter 5). Here we are
guided by the facts (which will be explained later) that if F is the image that is
eventually drawn by the IFS W, then W(F) = F. Now, W is made up of
several affine transformations wi of the form wi = A + v where A
is a matrix and v
is a vector (the shift); W = w1 U w2 U . . .
wk (here, U denotes union - see page 238). So W(F) = F means that F = F1
U F2 U . . . U Fk where Fi = wi(F).
Since each Fi is a smaller copy of F (and perhaps rotated, reflected, or
sheared or a combination of these), we see that F is the union of
smaller (perhaps distorted) copies Fi of itself: the IFS builds in the self-similarity of F.
This allows us to find an IFS that draws F: break up F into k self-similar
pieces Fi. Then figure out what the affine transformation wi
are such that wi(F) = Fi.
We use the parameters a,b,c,d,e,f
to define an affine transformation w = A + v, where a,b,c,d are the entries of the
matrix A (a=A11, b=A12, c=A21, d=A22),
and e,f are the components of the vector v; v = (e,f). See page 295 in the text for
a listing of the paramenters for the various IFS that draw the fractals in that chapter. See also Section 3.4 and the
28 January commentary for W00.
See here for examples of iterates of various IFS.
I did some experiments/examples of IFS's using the applets and VB
programs available on the course webpage. Using the VB program Fractal Pattern,
we saw the iteration of the IFS's that produce the Sierpinski triangle, the von Koch and
square von Koch curves, and the Fern. We also looked at the IFS for the Cantor set and the
Cantor line set (Cantor set stretched into lines). The parameters for these two IFS's are
(since they are not in the menu);
- Cantor set:
- 1: (a, b, c, d, e, f, p) = (0.334, 0, 0, 0.334, 0, 0.334, 0.5)
- 2: (a, b, c, d, e, f, p) = (0.334, 0, 0, 0.334, 0.667, 0.334, 0.5)
- Cantor lines:
- 1: (a, b, c, d, e, f, p) = (0.334, 0, 0, 1, 0, 0, 0.5)
- 2: (a, b, c, d, e, f, p) = (0.334, 0, 0, 1, 0.667, 0, 0.5)
Note that
the time taken to produce an image increases very quickly the more iterations you perform.
For transformations that have 3 lenses (labeled 1, 2, 3 in the program) you wouldn't want to
do more than 9 or so iterations. For 4 lenses you wouldn't want to do more than 8 or so iterations, and
for 5 lenses you wouldn't want to do more than 7 or so iterations. (Note that, since the small squares
are reduced at each iteration, in principle you would only iterate the IFS enough times so that
those squares became the size of a pixel on your monitor.) We saw that, unlike for the
Sierpinski triangle, von Koch curves, and Cantor set, the Fern fractal cannot be
drawn this way (too many iterations are required). We will see that the chaos game
is a more efficient way to draw fractals (Chapter 6).
I did some experiments with the Fractal Movie applet. In the Fractal Movie
applet you specify an initial (start pattern) IFS (or blueprint) and final (end pattern)
IFS.
The applet then interpolates
between the two, drawing the fractal produced by the intermediatary IFS's. For the first
experiment I simply took as initial IFS the Sierpinski IFS with top lens (#3) sitting all
the way to the left and final IFS the Sierpinski IFS with lens #3 all the way to the right. The
parameters were (only parameters for lens #3 need to be adjusted from the Sierpinski IFS
parameters obtained from the drop down menu);
- start 3: (a, b, c, d, e, f, p) = (0.5, 0, 0, 0.5, 0, 0.5, 0.334)
- end 3: (a, b, c, d, e, f, p) = (0.5, 0, 0, 0.5, 0.5, 0.5, 0.334)
Another experiment illustrated
the various 'relatives of the Sierpinski gasket' (see pages 244-251). I took as
initial IFS the Sierpinski triangle and as final IFS the IFS obtained by rotating the top
lens (#3) by 90 degrees counter clockwise. We saw the Sierpinski triangle 'break apart' before
forming another fractal. The parameters here were (again, only lens #3 needs to be changed);
- start 3: (a, b, c, d, e, f, p) = (0.5, 0, 0, 0.5, 0, 0.5, 0.334)
- end 3: (a, b, c, d, e, f, p) = (0, -0.5, 0.5, 0, 0.5, 0.5, 0.334)
I showed the 'spiral' fractal. This IFS has two affine transformations (two lenses);
- 1: (a, b, c, d, e, f, p) = (0.85, -0.31, 0.31, 0.85, 0.2, -0.1, 0.5)
- 2: (a, b, c, d, e, f, p) = (0.35, -0.2, 0.2, 0.35, 0.5, 0.4, 0.5)
Lens #1 is contraction by a factor of about 0.9 and then rotation by about 20 degrees, and lens #2
is contraction by about 0.3 and then rotation by about 30 degrees (plus suitable shifts so the
resulting squares are within the original square). (Note that you can just imput these rotations
and scalings directly into the VB program (in this case the two angles are the same and the two
scaling factors r and s are the same) and ask it then to 'compute parameters' of the
resulting matrix, i.e., the a,b,c,d. See page 235 of the text for a description of how to define a
transformation (matrix) using these parameters instead of the a,b,c,d.) To get some idea of how
these two transformations together produce a spiral fractal, I did some experiments with the
Fractal Movie applet. Here the start IFS is the one above (note that you have to specify 'user'
in the drop down menu before you input the parameters). First I just made the second lens slide
horizontally and vertically. For the horizontal slide I took end parameters to be;
- end 2: (a, b, c, d, e, f, p) = (0.35, -0.2, 0.2, 0.35, -0.2, 0.4, 0.5)
(the end parameters for #1 remain the same as the start parameters). Here the spiral opens up
as the image of lens two moves out of the image of lens 1.
For the vertical slide I took end parameters to be;
- end 2: (a, b, c, d, e, f, p) = (0.35, -0.2, 0.2, 0.35, 0.5, 0, 0.5)
Here you will see the spiral 'tighten up' as the image of lens 2 moves into the centre of the
image of lens 1 (think about it; if the image of lens 2 was in the exact centre of the image
of lens 1, the resulting fractal would be just a point). Another experiment to perform to help
you understand how the IFS generates a spiral, is to rotate the lens 2. For a 90 degree
rotation of lens 2 take the end
parameters to be;
- end 2: (a, b, c, d, e, f, p) = (-0.2, -0.35, 0.35, -0.2, 0.7, 0.6, 0.5)
(To obtain these parameters I just multiplied the start 2 matrix by the matrix that represents
rotation by 90 degrees, and then adjusted the shift parameters so the resulting image remained in
roughly the same position as the start image.)
Here you will see that the rotation of lens 2 controls the orientation of the small curls on the
spiral fractal.
The Contraction Mapping Principle (see Section 5.6 and
Jan 28 2000 commentary): If f is a contraction on the
space X, then there exists a unique fixed point p of f, f(p) = p, and if x is any point in X then
f n(x) -> p as n -> infinity. If A is an (n by n) matrix such that ||Ax-Ay||< ||x-y||
for any vectors x and y,
then A is a contraction (on Rn). Since 0 is always a fixed point of any matrix,
Anx -> 0 for any vector x for such an A. An affine transformation w = A + v is
a contraction if and only if A is a contraction. Hutchinson's Theorem (p 268):
If the wi are contractions on R2, then the IFS W = w1
U w2 U . . . U wk is a contraction on the space X
of images (i.e., bounded subsets of R2) where distance between images is measured
by the Hausdorff distance (p 268). And so this is why an IFS that is made up
of contractions wi converges to an image F under iteration no matter
what image you start with. Note that the image F is the fixed point of the IFS.
To find the fixed point of an affine transformation w = A + v, solve the equation
w(p) = p; p = A(p) + v for p. To find the fixed point of an IFS W, iterate
W beginning with any image S. However, as we will see, it may take the IFS
a very long time to converge to the fixed point - so in the next chapter we will consider another
method to ind the fixed point (final image) of an IFS. This is the problem of decoding
an IFS (see page 259-260).
We defined the Hausdorff distance h(A, B) between two sets A and B: see pages
268 - 269. If e1 is the infimum of the set of e' s such that
B is contained in the set Ae, and e2 is the infimum of the set
of e' s such that A is contained in Be, then
h(A,B)= max {e1, e2} (see page 269). Here, the infimum of a set
(that is bounded from below) is the "bottom edge" of that set. Note that the infimum of a set may not
be in that set, for example, the infimum of the set (1,2) is 1 (see also page 216).
For example, the Husdorff distance between two points A={p} and B={q} is the
distance between the two points; h(A,B)=||p-q||. If a set B is contained in a set A, then
the set of all e' s such that B is contained in Ae is
(0, infinity), so the infimum of this set, e1, is 0. Now, suppose we remove a single
point from the set A, call this new set C, so that B is no longer contained in C (one point
of B is not covered by C). Then still e1 = 0 because still the
set of all e' s such that B is contained in Ce is
(0, infinity). In the example done in class today, A was a (solid) square with sides of length 2r
and B was the
(solid) disc of radius r enscribed within the square, the centre of the square and the centre of the disc
coinciding. Then h(A,B) = sqrt(2)r - r = e2 (note that e1=0).
Now, if C is the square minus the center point, then (still) e2 = sqrt(2)r-r and
e1=0, so h(C,B)=sqrt(2)r-r.
So we see that the Hausdorff distance does not distinguish between sets that are "too close"
together - for example, adding or removing finitely many points from one of the sets may not
change the Hausdorff distance between the sets (more about the consequence of this next time).
(Week of) 3 February
We discussed the Collage Game (Section 5.8). This is the problem of making an IFS that generates a certain image.
To begin with, we break-up the image into self-similar pieces and look for (affine) transformations
wi that produce these images.
In practice, the transformations wi are determinend interactively, i.e.,
by testing them to see what kind of image the IFS produces (see Fig 5.47) and then changing
the parameters (a, b, c, d, e, f) to obtain a better image. In addition to obtaining fractals
this way (in fact, the result will also be a fractal), one can obtain images that look
very much like `realistic' objects (see Fig 5.49 where an image of a leaf is reproduced by an
IFS with 7 lenses).
Decoding an IFS is the problem of drawing the image produced by an IFS
(see pages259-260 and 4 Feb W2000 commentary).
Recall that by Hutchinson's Theorem, if the wi are all contractions
on R2 with respect to the Euclidean metric (or norm, or distance;
these are all synonyms for metric), then the IFS W = w1 U
w2 U . . . U wk is a contraction on the space
X of images in R2 with respect to the Hausdorff metric, and
so iterating the IFS will ultimately lead to the fixed point F of the IFS.
However, the rate at which the iterates Wn(S) converge
to the image F delends on how much W contracts (with respect to
the Hausdorff metric). This could be so slow that it could take literally
forever to draw the fractal F this way. We can easily compute how
many iterations are required to draw the fractal F by first calculating how
many iterations are required for the initial image S (say, the unit square)
to be the size of one pixel (on your computer screen), and then calculating how
many images (squares, if S is a square) will be drawn after this many
iterations of the IFS. For Sierpinski, if S is a square 5002, then
because the contractions of the wi are 1/2, you need about 9
iterations before the initial square S is of size 1 (so, (1/2)9*500
<= 1). So the total number of squares drawn is 1 + 3 + 32 + . . .
+ 39 = (310-1)/(3-1) which is about 30,000. Assuming the computer can
draw 10,000 squares per second, the compter needs about 3 seconds to draw the Sierpinski
triangle. However, since the slowest contraction in the Ferm IFS is only .85, you
need about 39 iteations before the intial square S is 1 pixel small. The
number of squares drawn will 1 + 4 + 42 + . . . + 4 39
which is about 1023. To draw this many squares with your computer would
require more time than the age of the universe...... We will see in the next chapter
that another method to draw fractals, the Chaos Game, always works.
Fractal Image Compression. Compression means storing data on a computer
using the least amount of memory possible. Images contain a lot of data (8 bits per pixel
for grey-scale image, so a 512x512 pixel ('bitmap') image contains about 260KB (kilobytes;
1 byte is 8 bits) of data) so finding an efficient way to store them on a computer (and so
being able to electronically transmit them efficiently) is important. The JPEG image compression
standard can compress images by a factor of between 5 and 15 (depending on the image)
without perceptible distortion (so a 260KB bitmap image can be stored as JPEG file of
size around 18KB to 52KB). Fractal image compression takes advantage of the approximate self-similarity
present in most (natural) images. If an image was exactly self-similar, then you only
need the IFS that has that image as a fixed point to 'store' the image (everytime you want
to see the image you just run the IFS). An IFS is just a collection of numbers that define the
transformations wi, and they don't take up much memory. For example, the bitmap
of the Sierpinski triangle requires several hundred KB of data, the JPEG image would require
several 10's of KB of data, but the IFS requires only 3 x 6 = 18 numbers! (this is about 100 bytes)
Very roughly, the idea of fractal image compression is to partition the image into non-overlapping
'ranges' Ri (say, of size 4x4 pixels square) and then compare every 8x8 pixel square 'domain'
Dj of the image to each range Ri. Affine transformations wi
are applied to each domain Dj to try to match the Ri to Dj. Once a
satisfactory domain and transformation is found for that range Ri, you move on to the next
range Ri+1. When you are done with all the ranges you create a (big!) IFS
W = w1 U w2 U. . . U wk. When iterated (begining
with any initial image S) you will obtain an image that approximates the original image.
See the references for examples and more description. The best fractal image compression schemes have
compression ratios comparable to the best JPEG schemes today.
References: See S. Mallat's book A Wavelet Tour of Signal Processing, Second Ed. Section11.4
for more (technical) information about image compression. For fractal image compression
see Appendix A of the text (PJS), the books, Fractal Image Compression by Yuval Fisher, or
Fractal and Wavelet Image Compression Techniques by Stephen Welstead,
SPIE Optical Engineering Press, 1999, the U of Waterloo website http://links.uwaterloo.ca,
and the reports by Andrew Dagleish and Farhad Sadaghaini
.
See some examples of fractal image compression on the Fractal Image
Compression page.
We began the next chapter, Chapter 6: The Chaos Game. We have seen that iterating an IFS may
not be the best way to draw a fractal (in fact, the Fern fractal can not be drawn this way). The
problem there is that some wi of the IFS may contract too slowly.
A 'chaos
game' is an initial point z0, an IFS W = w1 U w2 U
. . . U wk, a set of probabilities p1, p2, . . . pk
(so 0 < pi < 1 and p1 + p2 + . . . + pk = 1),
and a 'random' sequence {s1, s2, . . . ,
sn} of numbers from the set {1, 2, ..., k} (i.e, each si is choosen
randomly from {1, 2, ..., k} according to the probabilities p1, ..., pk).
The sequence of points {z0, z1, . . . , zn}, where
zi = wsi(zi-1), is the outcome of the chaos game. We saw that several
thousand points zi are needed to see the fractal clearly (so n is usually
several tens of thousands - or even hundreds of thousands). The applets on the
software webpage use the chaos game to draw fractals.
(See the 21 Feb W2000 commentary for discussion of the chaos game.)
Some examples of using The Chaos Game method to draw fractals.
To understand why the chaos game 'works' (i.e., why it draws the fractal), we need to introduce the
notion of addresses on a fractal. If W = w1 U w2 U . . .
U wk is the IFS of the fractal F, then the region
wt1(wt2( ... wtm(F))...) (which we may sometimes write as
wt1wt2...wtm(F) - this is the composition of
the w's acting on F) of F has address
t1t2... tm. Note that you read an address from left to right
to locate the region with that address on the fractal,
but the transformations are applied from right to left. See pages 310-314 in the text.
Now note that if z is any point in the fractal F, then
wt1(wt2( ... wtm(z))...)
is a point in the region of the fractal that has address t1t2... tm
(because z is inside of F and the simple fact that if p is a point in a set A,
then w(p) is a point in the set w(A)). Thus, if we begin the chaos game with a point z0
in F, and if the random sequence {s1, s2, . . . , sn} is
used in the game (i.e., these si are the random numbers choosen), then
z1 is in the region of F with address s1 (because
z1 = ws1(z0)), z2 is in the region of F with
address s2s1 (because z2 = ws2(z1) =
ws2(ws1(z0))), z3 is in the region of F with
address s3s2s1 etc., and zn is in the region
of F with address snsn-1, . . . s2s1. So the
random sequence {s1, s2, . . . , sn} tells us the addresses of the
game points {z1, z2, . . . , zn} (but note that all we know about the
address of z1 is that it begins with s1, all we know about the
address of z2 is that it begins with s2s1, all we know about
the address of z3 is that it begins with s3s2s1,
etc; if we want more precise addresses of the game points than this we need to know the address of the
initial point z0).
A consequence of this is that if a certain string tmtm-1. . . t2t1
appears in the sequence {s1, s2, . . . , sn}, then we know that some
game point will land in the region of F with address t1t2. . . tm-1
tm.
Now we can explain why the game points {z1, z2, . . . , zn} eventually
(i.e., as n tends to infinity)
"fill" the fractal F. We will do the proof for the Sierpinski Chaos game.
To do this we pick any point p in T (the Sierpinski triangle) and any
small number d. We want to show that some game point lies within a distance d of p.
First pick m such that (1/2)m < d. Because each wi of the
Sierpinski IFS contracts by 1/2, any region on T with address of length k will be of
size (1/2)k, so any region of T with address of length m will be smaller than d. Let
t1t2. . . tm-1tm be the first m digits in the address of p.
Thus, p lies in the small triangle with address
t1t2. . . tm-1tm. Now, as explained above, if the string
tmtm-1. . . t2t1
appears in the sequence {s1, s2, . . . }, then some game point will land in
this small triangle with address t1t2. . . tm-1tm. Thus,
this game point will be within d of the point p (because this small triangle has size
(1/2)m). But why should the string
tmtm-1. . . t2t1 appear in {s1, s2, . . . }?
It appears because of the following fact about random sequences:
If p1, p2, . . . pk are the probabilities that the digits
1, 2, . . . , k are chosen randomly for the sequence {s1, s2, . . . },
then the string tmtm-1. . . t2t1 will appear in the sequence with
frequency ptmpt(m-1)...pt2pt1 (this is the product of the
probabilities ptm, pt(m-1), . . . , pt1.)
So as long as all the probabilities pi are non-zero, any and every (finite)
string will occur in the sequence {s1, s2, . . . } (because any product
of the probabilities will be > 0), and so there
will (eventually) be a game point that lands in that small triangle with address
t1t2. . . tm-1tm (the rub - and profound problem - is that,
although we know that any particular string will occur in the sequence,
we don't know where in the sequence it occurs, and so we don't know for sure how long we will have to wait before it occurs).
In short, a game point will land in every address region of the fractal because every string
that can be made from the digits {1,2,...,k} will appear (infinitely many times in fact!) in the sequence
{s1, s2, s3, . . . }.
See also page 317 in the text.
Some examples of using The Chaos Game method to draw fractals.
(Week of) 10 February
Recall that to play a Chaos Game, you need an IFS W = w1 U w2
U . . . U wk, a set of probabilities p1, p2, . . . , pk,
an initial game point z0, and a sequence of random numbers {s1,
s2, . . . , sn} where the si are chosen according to the
probabilities p1, p2, . . . , pk. Then one obtains the game
points {z1, s2, . . . , zn} according to the rule
zk+1 = ws_(k+1)(zk). All that was needed to prove that the game points
will eventually fill-out the fractal F (F is the fixed point of the IFS: W(F) = F) is
that every possible finite string of the digits 1, 2, ..., k appear in the sequence
{s1, s2, . . . } (we proved this using addresses of the fractal
F: the region Ft1...tm of F with address t1t2...
tm is the set Ft1...tm = wt1wt2...wtm(F)).
See the handouts page for some (more) notes on the chaos game. (Note:
The HW problems listed there are not to be handed in.)
The probability that a certain string, say tmtm-1...t1, appears
in the sequence {s1, s2, . . . }, is the product of probabilities
ptm pt(m-1)...t1. So for example, if p1=.2,
p2=.3 and p3= .4, then the probability that the string 213 appears
in {s1, s2, . . . } is p2p1p3 =
(.3)(.2)(.4) = .024 (so this string will occur, on average, 2.4% of the time, or about 24 times in
every sequence of length 1000). Note that this means that 2.4% of the game points will fall in the
region with address 312.
So we can estimate the number of game points needed to fill-out the
fractal on our computer screen. Suppose we are playing the chaos game with the Sierpinski IFS and
the fractal fills the screen 512 by 512 pixels. Each wi contracts by 1/2, so
regions on F with addresses of length k will be of size (1/2)k*(512). When this product is
1, the regions are of size one pixel so we can not discerne regions with addresses of longer lengths.
In this example, address of length 9 will be 1 pixel in size. So we only need from our random sequence
all strings of length 9 made from the digits 1, 2, 3. Then we will draw the Sierpinski as accurate
as our computer screeen allows. So how long must the random sequence
{s1, s2, . . ., sn} be so that it contains all strings of length 9?
Well, the probability that the string t9t8...t2t1
appears is pt9pt8...pt2pt1. Since all the probabilities
pi are equal to 1/3 (in this case), the probability that any string of length 9 will
appear in the random sequence {s1, s2, . . ., sn} is
(1/3)9 or about 1/20,000. So the length, n, should be around 20,000 (we will need about 20,000
game points to draw the Sierpinski triangle). See pages 316-317 in the text.
We considered the "full triangle" IFS on the Modified Chaos Game applet.
Here there are 4 lenses. The first 3 lenses are the same as in the Sierpinski IFS, and the fourth lens fills the
triangle in the centre. When we play this chaos game we will generate a random sequence
{s1, s2, . . ., sn} of digits from {1,2,3,4}.
Since the solid triangle is a fixed point of this IFS (check!), the game points of the
chaos game with this IFS will eventually fill-out the solid triangle (try it). Now, if we remove all the
4's from the sequence {s1, s2, . . ., sn} we will be left with
a (random) sequence of digits from {1,2,3}. This sequence with the full triangle IFS will produce the
Sierpinski triangle (since you will be doing the same thing as you would with the Sierpinski chaos game).
Removing all 4's from the sequence {s1, s2, . . ., sn} means that
no strings containg a 4 will occur, which in turn means that no game point will land in a region of the
full triangle with address containing a 4. If you think about it, removing all regions with addresses that
contains a 4 will leave you with exactly the Sierpinski triangle (so the Sierpinski triangle is the full triangle
minus all the regions with addresses that contain a 4). Now instead of removing all 4's from the
sequence {s1, s2, . . ., sn}, what happens if we remove all occurences
of the string '12'? Then no string that conntains a 12 will occur, which means no game point will land in
a region of the full triangle with address containing a 21 in it. For example, you will see 'holes' in the
full triangle that correspond to regions with address 21, 211, 213, 121, 1121, 2111, etc. See the
Modified Chaos Game applet and the figure there. If you look closely you
will see that this is NOT a fractal. But it has some kind of self-similarity.
We discussed how to express the game rules of a chaos game in plain English. That is, starting with an
IFS, can you write-down the game rules in plain English? To do this, we first expressed the affine
transformations wi = Ai + (ei, fi) in terms
of just Ai and the fixed point qi. Since wi(qi)
= qi, Ai(qi) + (ei, fi) = qi,
so that (ei, fi) = qi - Ai(qi).
So wi = Ai + qi - Ai(qi) - this is the
affine transformation expressed in terms of just Ai and qi. So the
mathematical chaos game rule zk+1 = wi(zk) can be written as
zk+1 = qi + Ai(zk-qi), which in English
says, "standing on qi, go to Ai(zk-qi) to
obtain zk+1" (you have to express the formula Ai(zk-qi)
in English).
The next topic is adjusting the probabilities in the chaos game (Section 6.3). Suppose we play the
chaos game with the Sierpinski IFS, but instead of using equal probabilities
p1 = p2 = p3 = 1/3 (like we have been), we use the probabilities
p1 = p2 = 0.2, p3 = 0.6. Then 3 will occur in the random
sequence {s1, s2, . . . } 3 times as often as a 1 or a 2 will occur.
Consequently, game points will land in the region with address 3 (the top part of the triangle) 3 times as
often as they will land in the regions with address 1 or 2. So playing the chaos game with these probabilities
will result in the top part of the Sierpinsli triangle filling out more quickly than the bottom parts (try
this with the applet, or look at Figure 6.21 on page 324 of the text, and the
Chaos Game with Varying Probabilities page given below).
The proof that the chaos game draws the fractal only used the property that the
probabilities are non-zero, so the Sierpinski triangle WILL be drawn - but it will take a lot longer to
draw than if equal probabilities were used. We can go on. The string 13 will occur 3 times as often in
{s1, s2, . . . } as the string 12, so 3 times as many game points will land
in the region with address 31 than in the region with address 21. The string 133 will occure 9 times as
often in {s1, s2, . . . } as the string 122, so 9 times as many game
points will land in the the region with address 331 than in the region with address 221, etc. These kind
of calculations explain the image you see when you run the applet with these probabilities.
See the Chaos Game with Varying Probabilities page for some
examples of fractals drawn with the chaos game using unusual probabilites.
I ran the chaos game using the full square IFS (i.e., an IFS with 4 lenses whose blueprint fills
the initial square). The fixed point of this IFS is clearly the full square. Since all contractions
are equal, the best probabilities used to draw this fractal are the equal ones;
pi = 1/4. We know that the chaos game with any (non-zero) probabilities
will (eventually) draw the full square, but you get vastly different intermediate patterns if you
choose non-equal probabilities. For example, choose instead p1=p2=.4 and
p3=p4=.1 (here, lens 1 is in the bottom left corner, lens 2 is in the
top left corner, lens 3 is in the top right corner, and lens 4 is in the bottom right corner - just
as they are on the Chaos Game and Fractal Movie applets), you will see a whole series of vertical lines.
We can understand this pattern by realizing that most of the time, the sequence is just 1's and 2's (in fact
80% of the time) so points will move towards the fixed point (the line) of the IFS made of just
lens 1 and 2. But whenever a 3 or 4 comes along in the sequence, the game point (which is lying very
near that vertical line on the left edge) will jump towards one of the corners on the right edge
of the square (these are the fixed points of the lenses 3 and 4). They will move 1/2 the distance towards
them, in fact (lenses are contractions by 1/2). Thus, they will lie along the vertical line at
x = 1/2. The vertical line at x=3/4 is caused by game points on the line x=1/2 under one of the
transformations 3 or 4 (which move them again 1/2 the distance towards the fixed points). That's
why you see a whole series of vertical lines at x=1/2, x=3/4, x=7/8, x=15/16, .... Homework
problem #11 in Homework #3 is similar to this.
We discussed playing the chaos game with the Sierpinski IFS using the sequence s = {1,2,3,1,2,3,1,2,3,.....}
(that is, 123 repeating). Suppose the initial game point z0 is somewhere inside the
full triangle T0. Then the addresses of the game points {z1, z2,
z3, ....} are 1_ _ , 21_, 321, 1321, 21321, 321321, 1321321, .... .
We see that the game points are approaching the three points p1, p2,
p3 with addresses 32132132...., 213213213.....,
and 132132132..... (because the addresses of the game points are agreeing more and more with the addresses
of these three points as the game proceeds). Now, playing the chaos game with the sequence s = {1,2,3,1,2,3....}
is like applying the transformation w321 = w3w2w1 over and
over again beginning with the initial game point z0, or like applying the transformation
w213 = w2w1w3 beginning with the second game point
z1, or like applying the transformation w132 = w1w3w2
to the third game point z2. So those three points are the fixed points of these three (contractive, affine)
transformations; w321(p1)=p1, w213(p2)=p2,
w132(p3)=p3 (note that applying anyone of these three transformations shifts
the address of a point to the right by three places, so check that the addresses of these fixed points is unchanged
when the transformation is applied to it).
Adjusting probabilities (see Section 6.3 in the text).
For IFS whose transformations have all the same
rate of contraction, we saw that when the probabilities are all equal the
fractal is drawn most efficiently (over other, non-equal probabilities).
However, if the transformations have differing rates of contractions, then
we gave heuristic arguments to show that, at least in some approximation,
that choosing the probabilities pi such that the ratios p1/c1,
p2/c2, ... , pk/ck are all equal, and that
p1 + p2 + . . . pk = 1 (so that the pi's are
probabilities)
gave a good impression of the fractal (here we are
considereing regions of address length 1).
Here ci = |det Ai|,
the absolute value of the
determinent of the matrix Ai of the transformation wi,
is the factor by which wi
changes areas. The argument was to make the densities of points
in the parts of the fractal with addresses of equal length
the same.
(Density is number of points/ area of region; if N is the number of game points
used in the game, then the number of points in the region with address i is pi*N, and
if a is the area of the filled in fractal FF,
then the area of the region with address i is area of(wi(FF)) = ci*area of(FF)
= ci*a (see Figure 5.38 on page 280 of the text),
so density = (pi*N)/(ci*a); when we equate these together, we can cancel out the
common factors N and a; that's why we only need to consider the ratios
pi/ci.)
We calculated a 'first approximation' to the 'best' probabilities for drawing the Fern with the chaos game by
choosing probabilities so that the densities of game points in regions of the fractal with address length 1
are equal. We took the IFS given in the Chaos Game applet. The areas of
the regions of address length 1 are proportional to the absolute values of the detrminant of the matrix for
that affine transfomation; for the transformations w1, w2, w3, w4
we have c1=0, c2=.10, c3=.12, c4=.48, where ci
is the absolute value of the determinant of the matrix Ai. Note that c1=0 (bcause
w1 contracts area to a line), so we just set p1=0.02 (we could adjust this value
later if we think it would help). Then the equations that say that the densities of points in regions with
address 2, 3, and 4
are equal are; p2/c2 = p3/c3 = p4/c4.
We also have the equation p1 + p2 + p3 + p4 = 1 (probabilities
must add to 1). Solving these equations we find; p1=.02, p2=.14, p3=.17,
and p4=.67. Drawing the fern with these probabilities is much more efficient than
with equal probabilities pi=1/4.
In class we calculated the
probabilities which gives equal densities of game points for all regions of the fern with address
length 1. However, even though the adjusted probabilities insure that the density of game points in each
region of address length 1 have equal densities, the densities of points within those regions (i.e.,
regions of address lengths greater than 1) may have non-equal densities. If you want to insure, in addition,
that regions of address length 2 have equal densities, then you will have to solve the equations
(p1p2/c1c2) =
(p1p3/c1c3) =
. . . . We also have to require that p1 + p2 + . . . pk = 1.
See pages 327-329, and Section 6.5 of the text for a discussion of the 'Adaptive Cut' method for drawing the
fractal very efficiently with the chaos game.
Playing the chaos game with sequences that are not random.
See the
Chaos Game with Non Random Sequences handout.
Recall that the only property needed of the sequence {si} in order that
the fractal gets drawn when using this sequence in the chaos game,
was that it contain every possible string of the integers {1,..., k} (where the
IFS has k transformations). Actually, if your computer screen can
only resolve detail down to level 'm' (i.e., addresses of length m are the
smallest areas you can see; they are about one pixel in size), then you only
need a sequence that contains all possible strings of length m (then a point
will land in each of these addresses when the chaos game is played with that
sequence). One can write down a sequence that contains all strings of length
m; the 'naive' sequence will be of length kmm . However, there will be
a lot of redundancy from using such a string in the chaos game (for
example, suppose we want to draw Sierpinski triangle to level 3, then the
naive sequence has 33 3 = 81 numbers, from which we will obtain 81 points.
However, there are only 27 addresses of length 3, so we only need 27
points). There are 'best' sequences that have no redundancies.
Such sequences have length km + m-2. Note this is about km
for moderately large m, which is smaller by a factor of m than the
length of the 'naive' sequences.
How well do random sequences do? As explained in the handout (and as you will see if you do Problem
# 16 on Homework #3), they do an intermediate job. That is, to draw a fractal to a certain degree
of completeness, the length of a random sequence needed to do this will be longer than the 'efficient'
(or 'best')
one but shorter than the 'naive' one.
Some references about these topics;
- A Probabilist Looks at the Chaos Game, by Gerald Goodman, in
the book, Fractals in the Fundamental and Applied Sciences,
edited by H.-O. Peitgen, J.M. Henriques, and L.F. Penedo.
- Rendering Methods for Iterated Function Systems, by
D. Hepting, P. Prusinkiewicz, and D. Saupe in the same book as
above.
End of Fractal section of course.
Summary for Dynamics
