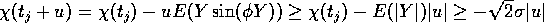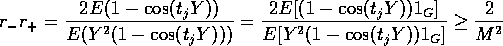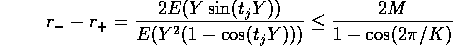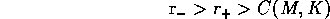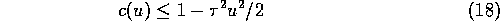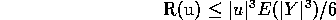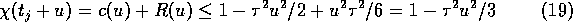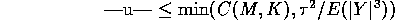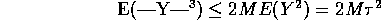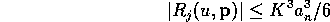References



Next: About this document
Up: Maximum likelihood estimation of
Previous: Discussion
- N. Becker (1977). Estimation for discrete-time branching
processes
with applications to epidemics. Biometrics 33, 515-
522.
- I. J. Bienaymé (1845). De la loi de multiplication et de la
durée
des familles. Soc. Philomath. Paris 5, 37-39.
- L. F. B. de Châtauneuf (1847). Mémoire sur la durée
des familles nobles de France. Memoire de l'Académie royale
des sciences morale et politiques de l'Institut de France 5,
753-794.
- A. P. Dempster, N. M. Laird, and D. B. Rubin (1977).
Maximum likelihood from incomplete data via the EM algorithm.
J. Roy. Statist. Soc. Ser. B 39, 1-38.
- J.-P. Dion (1974). Estimation of the mean and the initial
probabilities of a
branching process. J. Appl. Prob. 11: 687-694.
- J.-P. Dion (1975). Estimation of the variance of a branching
process. Ann. Statist. 3, 1183-1187.
- J.-P. Dion, G. Labelle, and A. Latour (1982).
Small sample results for maximum-likelihood estimation in
branching processes.
Can. J. Statist. 10, 271-276.
- C. Duby and A. Rouault (1982). Estimation non paramétrique
de
l'espérance et de la variance de la loi
de reproduction d'un processus de ramification.
Ann. Inst. Henri Poincaré XVIII B, 149-163.
- W. Eschenbach and W. Winkler (1975). Maximum-Likelihood-
Schätzungen
beim Verzweigungsprozess von Galton-Watson. Math. Op. forsch.
Statist.
6, 213-224.
- W. J. Ewens (1969). Population genetics. London:
Methuen.
- P. D. Feigin (1977). A note on maximum likelihood estimation
for simple
branching processes. Austr. J. Statist. 19, 152-154.
- P. Guttorp (1991). Statistical inference for branching
processes.
New York: Wiley.
- T. E. Harris (1948). Branching processes. Ann. Math.
Statist. 19,
474-494.
- C. C. Heyde (1974). On estimating the variance of the offspring
distribution
in a simple branching process. Adv. Appl. Prob. 3, 421-
433.
- N. Keiding and S. Lauritzen (1978). Marginal maximum
likelihood estimates and
estimation of the offspring mean in a branching process.
Scand. J. Statist. 5, 106-110.
- D. G. Kendall (1951). Some problems in the theory of queues.
J. Roy. Statist. Soc. ser. B 13, 151-185.
- N. Keyfitz (1985). Applied mathematical demography (2
ed.).
New York: Springer.
- R. A. Lockhart (1982). On the nonexistence of consistent
estimates in
Galton-Watson branching processes. J. Appl. Prob. 19,
842-846.
- T. R. Malthus (1817). An essay on the principle of
population, as
it affects the future improvements of society, with remarks on
the speculations of Mr. Godwin, M. Condorcet, and other writers (5
ed.).
London: John Murray.
- T. J. Sweeting (1986). Asymptotic conditional inference for
the offspring
mean of a supercritical Galton-Watson process. Ann. Statist.
14,
925-933.
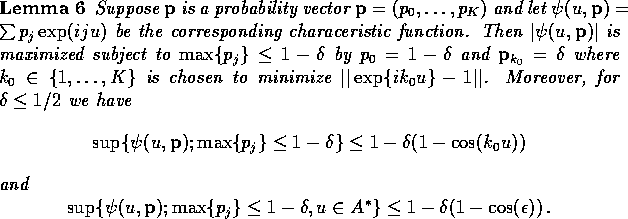
Proof of Lemma 6:
The set of values of

as

ranges over the set of probability
vectors satisfying the constraint is a convex polygon. Since the modulus function is convex
the supremum is achieved at some extreme point. The extreme points consist of
those two point distributions putting mass

and

on adjacent
vertices of the polygon. If such a distribution puts mass on

and

then the same norm is achieved by putting the same masses on

and 1. It is then easy to check that the norm is the same for
the masses

and

as for the masses

and

.
Proof of Lemma 7:
Our proof is via a symmetrization argument. If

is independent of

and has the same distribution as

then

is bounded by

, has mean 0 and variance

.
The characteristic function of

is

.
Thus (16) follows from
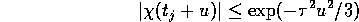
for all

.
The characteristic function

is real and has the expansion
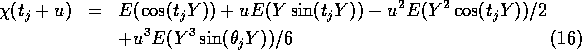
where

lies between

and

.
Denote by

the quadratic function on the right hand side of
 and by
and by

the remainder.
We will prove that

for all

; in view of the inequality

this would finish the proof.
If

then
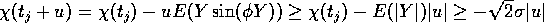
.
For

, since

we then have

Since

we see that this inequality holds for all

.
On the other hand the quadratic

is non-negative at

. If

then

almost surely. Hence

almost
surely and

for all

. If

then

is non negative between its two roots

and

. Let

denote the event that

. Then the roots satisfy
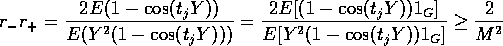
and
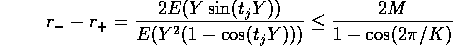
It is now easily checked that
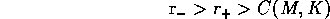
. Hence
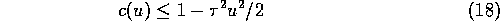
for all

. Now use
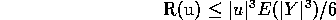
to check that
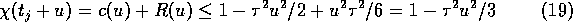
for all
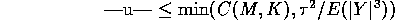
. Next
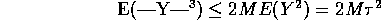
so that

.
Thus we see that

implies
( ).
).
The case

is handled with the roles of

and

reversed.
It now follows from the lemma that

On the set

we have the Taylor expansion

where
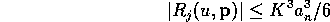
for every

.



Next: About this document
Up: Maximum likelihood estimation of
Previous: Discussion
Richard Lockhart
Thu Oct 26 23:26:04 PDT 1995
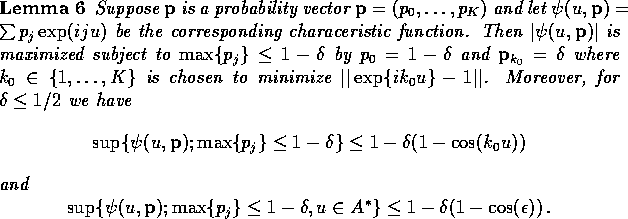



















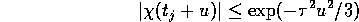






![]() and by
and by