Postscript version of these notes

STAT 801 Lecture 23

Reading for Today's Lecture:

Goals of Today's Lecture:

• Introduce confidence sets.

• Describe relation of tests to confidence intervals.

• Describe the use of pivots to make confidence sets.

• Introduce decision theory.

Today's notes

Confidence Sets

A level $\beta$ confidence set for a parameter $\phi(\theta)$is a random subset C, of the set of possible values of $\phi$ such that for each $\theta$ we have

$$P_\theta(\phi(\theta) \in C) \ge \beta$$

Confidence sets are very closely connected with hypothesis tests:

Suppose C is a level $\beta=1-\alpha$ confidence set for $\phi$. To test $\phi=\phi_0$ we consider the test which rejects if $\phi\not\in C$. This test has level $\alpha$. Conversely, suppose that for each $\phi_0$ we have available a level $\alpha$ test of $\phi=\phi_0$ who rejection region is say $R_{\phi_0}$. Then if we define $C=\{\phi_0: \phi=\phi_0 \mbox{ is not rejected}\}$ we get a level $1-\alpha$ confidence for $\phi$. The usual t test gives rise in this way to the usual t confidence intervals

$$\bar{X} \pm t_{n-1,\alpha/2} \frac{s}{\sqrt{n}}$$

which you know well.

Confidence sets from Pivots

Definition: A pivot (or pivotal quantity) is a function $g(\theta,X)$ whose distribution is the same for all $\theta$. (As usual the $\theta$ in the pivot is the same $\theta$ as the one being used to calculate the distribution of $g(\theta,X)$.

Pivots can be used to generate confidence sets as follows. Pick a set A in the space of possible values for g. Let $\beta=P_\theta(g(\theta,X) \in A)$; since g is pivotal $\beta$ is the same for all $\theta$. Now given a data set X solve the relation

$$g(\theta,X) \in A$$

to get

$$\theta \in C(X,A) \, .$$

Example: The quantity

$$(n-1) s^2/\sigma^2$$

is a pivot in the $N(\mu,\sigma^2)$ model. It has a $\chi_{n-1}^2$distribution. Given $\beta=1-\alpha$ consider the two points $\chi_{n-1,1-\alpha/2}^2$ and $\chi_{n-1,\alpha/2}^2$. Then

$$P(\chi_{n-1,1-\alpha/2}^2 \le (n-1) s^2/\sigma^2 \le \chi_{n-1,\alpha/2}^2) = \beta$$

for all $\mu,\sigma$. We can solve this relation to get

$$P( \frac{(n-1)^{1/2} s}{ \chi_{n-1,\alpha/2}} \le \sigma \le \frac{(n-1)^{1/2} s}{ \chi_{n-1,1-\alpha/2}}) = \beta$$

so that the interval from $(n-1)^{1/2} s/\chi_{n-1,\alpha/2}$ to $(n-1)^{1/2} s/\chi_{n-1,1-\alpha/2}$ is a level $1-\alpha$ confidence interval.

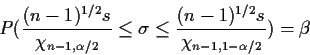
In the same model we also have

$$P(\chi_{n-1,1-\alpha}^2 \le (n-1) s^2/\sigma^2 ) = \beta$$

which can be solved to get

$$P(\sigma \le \frac{(n-1)^{1/2} s}{ \chi_{n-1,1-\alpha/2}}) = \beta$$

This gives a level $1-\alpha$ interval $(0,(n-1)^{1/2} s/\chi_{n-1,1-\alpha})$. The right hand end of this interval is usually called a confidence upper bound.

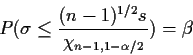
In general the interval from $(n-1)^{1/2} s/\chi_{n-1,\alpha_1}$ to $(n-1)^{1/2} s/\chi_{n-1,1-\alpha_2}$has level $\beta = 1 -\alpha_1-\alpha_2$. For a fixed value of $\beta$ we can minimize the length of the resulting interval numerically. This sort of optimization is rarely used. See your homework for an example of the method.