Reading for Today's Lecture:
Goals of Today's Lecture:
Today's notes
Theorem: In testing f0 against f1 the probability
![]() of a type II error is minimized, subject to
of a type II error is minimized, subject to
![]() by the test function:
by the test function:
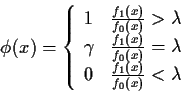
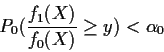
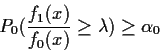
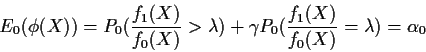
Definition: In the general problem of testing
![]() against
against ![]() the level of a test function
the level of a test function
![]() is
is
Example: In the Binomial(n,p) to test p=p0 versus
p1 for a p1>p0 the NP test is of the form
Example: In the ![]() example to test
example to test
![]() against
against
![]() for some
for some
![]() the NP test is of the
form
the NP test is of the
form
Proof of the Neyman Pearson lemma: Given a test ![]() with level strictly less than
with level strictly less than ![]() we can define
the test
we can define
the test
For each
![]() we have seen that
we have seen that
![]() minimizes
minimizes
![]() where
where
![]() .
.
As ![]() increases the level of
increases the level of
![]() decreases from 1
when
decreases from 1
when ![]() to 0 when
to 0 when
![]() .
There is thus a
value
.
There is thus a
value ![]() where for
where for
![]() the level is less than
the level is less than
![]() while for
while for
![]() the level is at least
the level is at least ![]() .
Temporarily let
.
Temporarily let
![]() .
If
.
If
![]() define
define
![]() .
If
.
If
![]() define
define
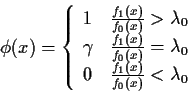
Now ![]() has level
has level ![]() and according to the theorem above
minimizes
and according to the theorem above
minimizes
![]() .
Suppose
.
Suppose ![]() is some other
test with level
is some other
test with level
![]() .
Then
.
Then
The examples show a phenomenon which is somewhat general.
What happened was this. For any
![]() the likelihood
ratio
the likelihood
ratio ![]() is an increasing
function of
is an increasing
function of ![]() .
The rejection region of the NP test is thus
always a region of the form
.
The rejection region of the NP test is thus
always a region of the form
![]() .
The value of the constant
k is determined by the requirement that the test have level
.
The value of the constant
k is determined by the requirement that the test have level ![]() and this depends on
and this depends on ![]() not on
not on ![]() .
.
Definition: The family
![]() has monotone likelikelood ratio with respect to a statistic T(X)if for each
has monotone likelikelood ratio with respect to a statistic T(X)if for each
![]() the likelihood ratio
the likelihood ratio
![]() is a monotone increasing function of T(X).
is a monotone increasing function of T(X).
Theorem: For a monotone likelihood ratio family the
Uniformly Most Powerful level ![]() test of
test of
![]() (or of
(or of
![]() )
against the alternative
)
against the alternative
![]() is
is
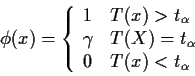
A typical family where this will work is a one parameter exponential
family. In almost any other problem the method doesn't work and there
is no uniformly most powerful test. For instance to test ![]() against the two sided alternative
against the two sided alternative
![]() there is no UMP level
there is no UMP level
![]() test. If there were its power at
test. If there were its power at ![]() would have to be
as high as that of the one sided level
would have to be
as high as that of the one sided level ![]() test and so its rejection
region would have to be the same as that test, rejecting for large
positive values of
test and so its rejection
region would have to be the same as that test, rejecting for large
positive values of
![]() .
But it also has to have power as
good as the one sided test for the alternative
.
But it also has to have power as
good as the one sided test for the alternative
![]() and
so would have to reject for large negative values of
and
so would have to reject for large negative values of
![]() .
This would make its level too large.
.
This would make its level too large.
The favourite test is the usual 2 sided test which rejects for large values
of
![]() with the critical value chosen appropriately.
This test maximizes the power subject to two constraints: first, that
the level be
with the critical value chosen appropriately.
This test maximizes the power subject to two constraints: first, that
the level be ![]() and second that the test have power which is
minimized at
and second that the test have power which is
minimized at ![]() .
This second condition is really that the
power on the alternative be larger than it is on the null.
.
This second condition is really that the
power on the alternative be larger than it is on the null.
Definition: A test ![]() of
of ![]() against
against
![]() is unbiased level
is unbiased level ![]() if it has level
if it has level ![]() and,
for every
and,
for every
![]() we have
we have
When testing a point null hypothesis like ![]() this requires
that the power function be minimized at
this requires
that the power function be minimized at ![]() which will mean that
if
which will mean that
if ![]() is differentiable then
is differentiable then
We now apply that condition to the ![]() problem. If
problem. If ![]() is any test function then
is any test function then
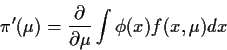
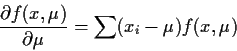
Consider the problem of minimizing
![]() subject to
the two constraints
subject to
the two constraints
![]() and
and
![]() .
Now fix two
values
.
Now fix two
values
![]() and
and ![]() and minimize
and minimize
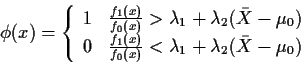
The likelihood ratio f1/f0 is simply
Now you have to mimic the Neyman Pearson lemma proof to check
that if ![]() and
and ![]() are adjusted so that the
unconstrained problem has the rejection region given then the
resulting test minimizes
are adjusted so that the
unconstrained problem has the rejection region given then the
resulting test minimizes ![]() subject to the two constraints.
subject to the two constraints.
A test ![]() is a Uniformly Most Powerful Unbiased level
is a Uniformly Most Powerful Unbiased level ![]() test if
test if
Conclusion: The two sided z test which rejects
if
What good can be said about the t-test? It's UMPU.
Suppose
![]() are iid
are iid
![]() and that
we want to test
and that
we want to test ![]() or
or
![]() against
against ![]() .
Notice that
the parameter space is two dimensional and that the boundary
between the null and alternatives is
.
Notice that
the parameter space is two dimensional and that the boundary
between the null and alternatives is
If a test has
![]() for all
for all
![]() and
and
![]() for
all
for
all
![]() then we must have
then we must have
![]() for all
for all ![]() because the power function of any test must
be conntinuous. (This actually uses the dominated convergence
theorem; the power function is an integral.)
because the power function of any test must
be conntinuous. (This actually uses the dominated convergence
theorem; the power function is an integral.)
Now think of
![]() as a
parameter space for a model. For this parameter space you
can check that
as a
parameter space for a model. For this parameter space you
can check that
Now let us fix a single value of ![]() and a
and a
![]() .
To make our notation simpler I take
.
To make our notation simpler I take ![]() .
Our observations above permit us to condition on S=s. Given
S=s we have a level
.
Our observations above permit us to condition on S=s. Given
S=s we have a level ![]() test which is a function of
test which is a function of
![]() .
.
If we maximize the conditional power of this test for each s then
we will maximize its power. What is the conditional model
given S=s? That is, what is the conditional distribution of
![]() given S=s? The answer is that the joint density of
given S=s? The answer is that the joint density of
![]() is of the form
is of the form
This makes the conditional density of ![]() given S=s of the form
given S=s of the form
![\begin{displaymath}T=\frac{n^{1/2}\bar{X}}{\sqrt{n[S/n-\bar{X}^2]/(n-1)}}
\end{displaymath}](img125.gif)